Уравнение неразрывности идеальной жидкости в дифференциальной форме

При изучении движения жидкости интенсивность массовых сил 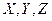обычно считается известной. Неизвестными являются функции 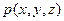, , 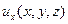, 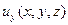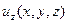– всего четыре неизвестных функции. Определяемые функции должны удовлетворять уравнениям Эйлера (6.5). Поскольку число неизвестных превышает число уравнений, к уравнениям Эйлера необходимо присоединить уравнение неразрывности в дифференциальной форме.

Уравнение неразрывности, записанное для элементарного объема жидкости в форме прямоугольного параллелепипеда размерами 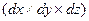(см. рис.6.1) можно получить на основании следующих рассуждений.

Гипотеза сплошности, применительно к идеальной жидкости, предполагает, что за время 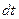объемы жидкости втекающей и вытекающей из элементарного параллелепипеда должны быть равны. Объемы жидкости втекающей через грани перпендикулярные осям 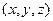легко найти по составляющим скорости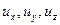

.

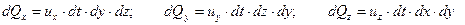(6.28)

Аналогичные объемы вытекающей жидкости, с учетом изменения скорости, равны

.

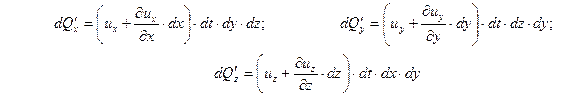(6.29)

Сплошность в рассматриваемом объеме не нарушится, если

,

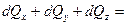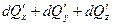(6.30)

что после подстановки (6.28) и (6.29) в (6.30) приводит к результату

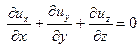
(6.31)

Уравнение (6.30) и есть уравнение неразрывности идеальной несжимаемой жидкости в дифференциальной форме.

Присоединив к уравнениям равновесия (6.5) уравнение неразрывности (6.31) получаем систему дифференциальных уравнений для определения четырех функций, характеризующих установившееся движение жидкости.

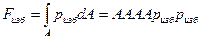
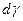
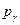
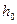
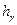
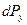
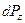
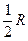
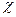
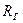
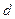
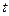
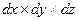
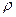
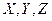
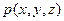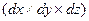
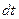
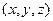
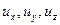
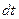
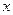
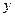
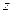
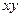– О

Уравнение Бернулли для струйки в поле силы тяжести

Если ось 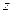направить по линии действия силы тяжести вверх, то из (6.12) получим

, , ,

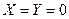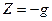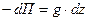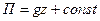
(6.32)

и уравнение (6.15) принимает вид

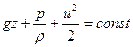
(6,33)

или

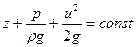
(6.34)

Если записать уравнение Бернулли для частицы жидкости при установившемся движении в двух ее положениях на линии тока (она совпадает с траекторией), то получим

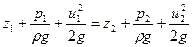
(6.35)