Поток жидкости. Понятия и характеристики

Гидродинамика. Основные понятия и определения

Гидродинамика – раздел гидравлики, изучающий движение жидкости в зависимости от сил к ней приложенных, ее взаимодействие с твердыми телами и стенками, ограничивающими ее движение.

Жидкость рассматривается как континуум, состоящий из частиц. В процессе движения изменяются взаимное расположение частиц жидкости и их форма. Последнее зависит от свойств, которыми наделяется жидкость. Если жидкость предполагается идеальной, то форма частиц изменяется только за счет формы канала в котором происходит движение. Если жидкость способна сжиматься и обладает вязкостью, то форма частиц изменяется не только за счет взаимодействия со стенками канала, но и в результате взаимодействия частиц друг с другом, которое характеризуется нормальными и касательными напряжениями на гранях выделенного элементарного объема.

Существует два способа описания движения жидкости: способ Лагранжа и способ Эйлера.

Способ Лагранжа предполагает рассмотрение движения каждой частицы жидкости. При этом

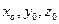- начальные координаты частицы;

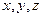- координаты частицы жидкости в произвольный момент времени 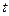, тогда:

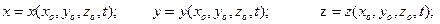
(5.1)

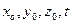- называют переменными Лагранжа.

Способ Эйлера предусматривает описание движения жидкости функциями, выражающими изменение скоростей в точках неподвижной области, выбранной в пределах потока (массы движущейся жидкости). По Эйлеру в точке рассматриваемой области, определяемой координатами 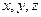, находится частица жидкости, имеющая скорость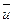

,

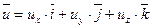(5.2)

где

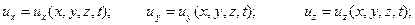
(5.3)

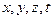- называют переменными Эйлера.

Совокупность формул (5.1) описывает траекторию движения частицы жидкости с начальными координатами 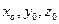. Используя эти уравнения можно найти проекции на координатные оси вектора скорости и вектора ускорения рассматриваемой точки.

Формулы (5.3) определяют в выбранной области (точка с координатами 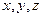) составляющие местной скорости в момент времени 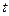. Эту скорость называют мгновенной местной скоростью. Совокупность мгновенных местных скоростей в рассматриваемой неподвижной области образует векторное поле – поле скоростей. В общем случае в каждый новый момент времени оно может измениться.

Линия, в каждой точке которой в данный момент времени вектор мгновенной местной скорости 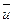направлен по касательной, называется линией тока (рис. 5.1).

Как следует из определения, составляющие скорости 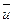, нормальные к линии тока, в любой точке этой линии равны нулю.

Если в рассматриваемый момент времени выделить в области, через которую движется жидкость, замкнутый, не пересекающий себя контур, то через каждую точку этого контура будет проходить только одна линия тока. Совокупность линий тока, проведенных через все точки этого контура, образует поверхность, которую называют трубкой тока. Жидкость, движущуюся внутри трубки тока, образует струйку. Внутри трубки жидкость движется не пересекая ее поверхности, т.к. скорости частиц направлены по касательным к линиям тока, образующим трубку. Если контур ограничивает бесконечно малую площадку 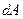, то струйку называют элементарной; если контур ограничивает конечную площадку 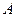, струйку называют конечной.

Рис. 5.1

Поверхность нормальная в каждой своей точке линиям тока называется живым сечением. Для элементарной струйки мгновенные местные скорости в пределах живого сечения можно считать одинаковыми и говорить о местной скорости элементарной струйки. Для конечной струйки значения местных скоростей в пределах живого сечения, как правило, не остаются постоянными. По длине струйки площадь живого сечения и мгновенные скорости могут изменяться.

Движение жидкости по характеру изменения во времени поля скоростей можно классифицировать на неустановившееся (нестационарное), когда местные скорости изменяются во времени (справедливы формулы (5.3)) и установившееся (стационарное), когда поле скоростей не изменяется

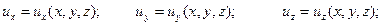
(5.4)

При установившемся движении траектории и линии тока совпадают, а в общем случае неустановившегося движения траектории и линии тока не совпадают. В частном случае неустановившегося движения, когда во времени изменяются только модули скоростей, а направления векторов не изменяются, линии тока и траектории также совпадают.

Необходимо подчеркнуть, что при установившемся движении струйки жидкости существуют физически, т.к. непроницаемые трубки тока неизменны во времени. При неустановившемся движении, в связи изменением поля скоростей, струйки являются только мгновенными, в силу того, что трубки тока непрерывно изменяются.

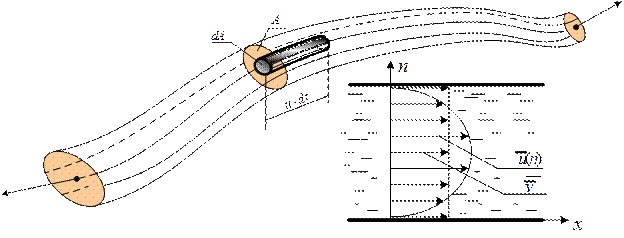
Расходом струйки называют объем жидкости, проходящей через живое сечение в единицу времени (рис. 5.2). Для элементарной струйки с равномерным распределением скорости по площади 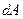имеем

.

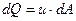(5.5)

Для конечной струйки при определении расхода необходимо учитывать изменение скорости движения частиц по площади живого сечения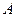

.

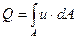(5.6)

Для упрощения расчетов целесообразно ввести понятие средней скорости в рассматриваемом живом сечении конечной струйки

,

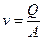(5.7)

и тогда расход можно определить как произведение средней скорости на площадь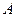

.

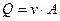(5.8)

Рис. 5.2

Поток жидкости. Понятия и характеристики

Потоком жидкости в гидравлике называют движущуюся массу жидкости, ограниченную твердыми поверхностями, поверхностями раздела жидкостей и свободными поверхностями. В зависимости от того какие поверхности ограничивают поток различают потоки безнапорные, напорные и гидравлические струи (рис. 5.3).

Безнапорный поток ограничен частично твердой, частично свободной поверхностью (масса воды в реке, в канале, трубе отвода стоков, рис.5.3а).

Напорный поток ограничен каналом, образованным твердыми поверхностями, все сечение которого заполнено жидкостью (вода в трубах системы водоснабжения, рис.5.3б).

Гидравлическая струя – это поток жидкости ограниченный только газовой средой или другой жидкостью (поток жидкости, выбрасываемый из пожарного брандспойта, рис.5.3в).

а) б) в)

Рис.5.3

На поток легко распространить введенные понятия: линия тока, трубка тока, элементарная струйка, живое сечение, объемный расход.

Площадь живого сечения потока рассматривается, как сумма площадей живых сечений элементарных струек

.

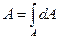(5.9)

Живое сечение потока может быть ограничено линией, часть точек которой соприкасается с твердыми стенками канала, направляющего движение жидкости. Длина этой части контура живого сечения называется смоченным периметром. На рис. 5.3а) и б) смоченный периметр показан тонкой прерывистой линией. На первом рисунке он равен ( 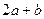), а на втором – ( 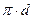). Обозначается смоченный периметр буквой греческого алфавита 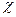(хи).

Отношение площади живого сечения к смоченному периметру называют гидравлическим радиусом

.

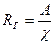(5.9)

Гидравлический радиус, это будет показано ниже – важная характеристика, используемая при определении расхода через живое сечение. В напорном потоке для круглого сечения диаметро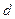м имеем

.

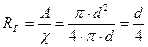(5.10)

Важной характеристикой потока является расход жидкости. Расход жидкости может определяться в единицах объема, единицах массы и единицах веса. Соответственно различают объемный, массовый и весовой расходы жидкости.

Расход жидкости – это количество жидкости протекающей через живое сечение в единицу времени. Согласно определению (см. (5.10)), расход измеряется в .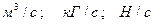

,

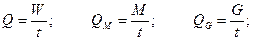(5.11)

где 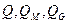- объемный, массовый и весовой расходы, соответственно;

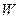- объем жидкости, протекающей через живое сечение потока за время ;

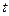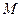- масса жидкости, протекающей через живое сечение потока за время ;

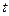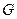- вес жидкости, протекающей через живое сечение потока за время .

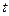Очевидно и то, что расход потока можно определить как сумму расходов элементарных струек, которые можно выделить в потоке

.

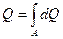(5.12)

Аналогично (5.7) и (5.8) определяется важная характеристика потока средняя скорость потока в рассматриваемом сечении

.

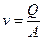(5.13)

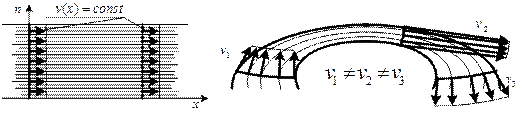
Введение понятия о средней скорости потока позволяет проще решать практические задачи. Важным с точки зрения практики является установившийся режим движения потока, который, в свою очередь подразделяют на равномерное и неравномерное движения.

а) б)

Рис. 5.4

Равномерное движение (рис.5.4а) характеризуется параллельностью и прямолинейностью линий тока, постоянством формы и размера живого сечения, средней скоростью по длине потока. Неравномерное движение (рис. 5.4б) отличается не параллельностью линий тока, изменением площади и формы живого сечения, изменением средней скорости по длине потока.

С практической точки зрения среди неравномерных движений выделяют плавно изменяющееся движение (рис.5.5), отличающееся следующими признаками: линии тока имеют малую кривизну, живые сечения можно считать плоскими, а их форма и площадь от сечения к сечению меняются плавно.

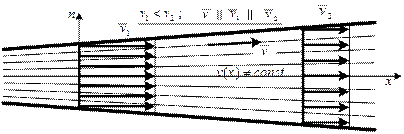Рис. 5.5

Средняя скорость в сечении – это условная скорость для всех точек потока в живом сечении, при которой обеспечивается реальный расход потока в заданном сечении. Используя понятие средней скорости потока, можно записать уравнение неразрывности потока несжимаемой жидкости

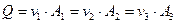.	(5.14)