Производные и дифференциалы функций нескольких переменных
Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х,у) и зададим приращение Dх к переменной х. Тогда величина Dx z = f(x+Dx,y)–f(x, y) называется частным приращением функции по х.Можно записать 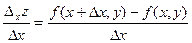 .
.
Тогда 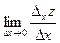 называется частной производнойфункции z = f(x, y) по х. Обозначение:
называется частной производнойфункции z = f(x, y) по х. Обозначение: 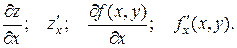
Аналогично определяется частная производная функции по у.
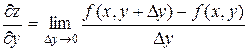
Геометрическим смысломчастной производной 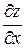 является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
Пример 4. Найти все производные первого порядка:
а)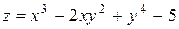 .
.
Решение. Рассматривая у как постоянную величину, получим 
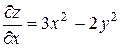 . Рассматривая х как постоянную величину, получим
. Рассматривая х как постоянную величину, получим 
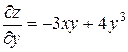 .
.
б) 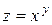 .
.
Решение. 
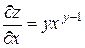 ;
; 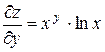 .
.
в) 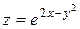 .
.
Решение. 
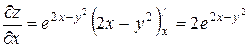 ;
; 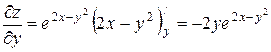 .
.
г) 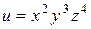 .
.
Решение. Рассматривая у и z как постоянные величины, получим 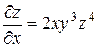 .
.
Рассматривая хи z как постоянные величины, получим 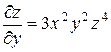 .
.
Рассматривая хи у как постоянные величины, получим 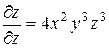 .
.
Пример 5.Показать, что функция 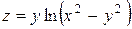 удовлетворяет уравнению
удовлетворяет уравнению 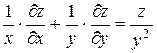 .
.
Решение. Находим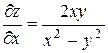 ,
, 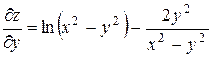 .
.
Подставим найденные выражения в левую часть уравнения:
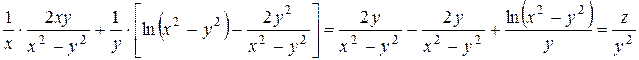
Пример 6.Найти 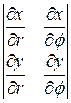 , если
, если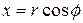 ,
, 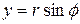 .
.
Решение. Находим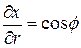 ,
, 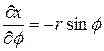 ,
, 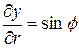 ,
, 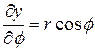 .
.
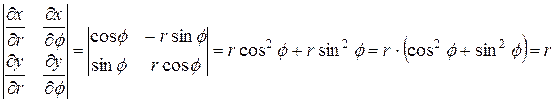 .
.
Дата добавления: 2017-12-05; просмотров: 471;
