АНАЛОГОВАЯ МИРОЭЛЕКТРОНИКА 4 страница
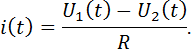
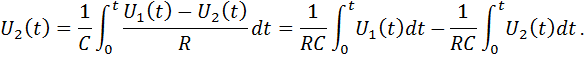
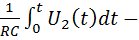 ошибка интегрирования, вызванная нелинейностью тока, протекающего через конденсатор.
ошибка интегрирования, вызванная нелинейностью тока, протекающего через конденсатор.
Используя преобразование Лапласа, перейдем к операторной форме записи
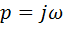
и рассмотрим интегрирующую цепь как цепь, образованную комплексными сопротивлениями
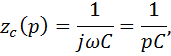
тогда получаем
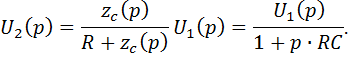
Коэффициент передачи цепи в операторной форме равен
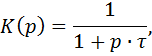
где 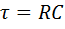 - постоянная времени цепи, а единица в знаменателе определяет ошибку интегрирования.
- постоянная времени цепи, а единица в знаменателе определяет ошибку интегрирования.
Активный интегратор на основе ОУ
получают включением конденсатора в цепь ООС.
| U1 |
| K0 |
| U2 |
| R |
| С |
| I1 |
| Iс |
Анализ интегратора на основе идеального ОУ дает результат, аналогичный с инвертирующим усилителем:
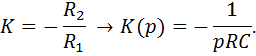
- отсутствует ошибка интегрирования.
Анализ интегратора на основе реального ОУ, для которого 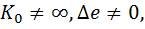 дает следующие результаты:
дает следующие результаты:
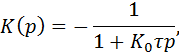
И показывает, что он ведет себя как инерционное звено первого порядка с коэффициентом усиления К0 и эквивалентной постоянной времени 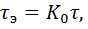 что уменьшает ошибку интегрирования в К0 раз.
что уменьшает ошибку интегрирования в К0 раз.
Рассмотрим физическую сущность процессов, происходящих в интеграторе. Для этого на вход подадим прямоугольный импульс.
На выходе идеального интегратора напряжение изменяется строго по линейному закону и после окончания импульса запоминается (остается постоянным).
| U1(t) |
| t |
| U2и(t) |
| t |
| Tи |
| U2р(t) |
| t |
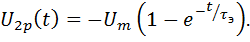
Если принять, что
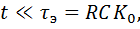
то нелинейностью можно пренебречь.
Однако за счет наличия напряжения смещения и входного тока ОУ после окончания входного импульса напряжение на выходе интегратора не останется неизменным – оно будет увеличиваться или уменьшаться. Таким образом, входные токи и напряжение смещения за счет накопления заряда могут создать на выходе большое напряжение и ввести ОУ в насыщение.
В практических схемах интеграторов предусматривают цепь разряда конденсатора через шунтирующее сопротивление или ключ, который замыкается в определенные моменты времени.
| U1 |
| K0 |
| U2 |
| R |
| R ш |
| С |
| Кл |
| K(ω) |
| ω |
| Kш |
| ←идеальный |
| ←реальный |
| ←пассивный |
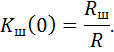
2. Дифференциатор
Простейшим пассивным дифференциатором является конденсатор, подключенный к источнику напряжения
| I(t) |
| U(t) |
| С |
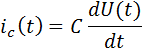
или в операторной форме
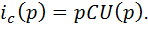
В качестве реального пассивного дифференциатора используют RC – цепь (дифференцирующую цепь)
| U2(t) |
| R |
| С |
| Ic(t) |
| U1(t) |
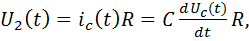
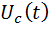 =
= 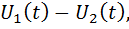
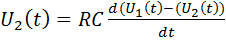 или
или
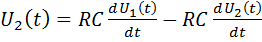 .
.
Второе слагаемое (вычитаемое) является ошибкой дифференцирования.
В операторной форме после преобразований получаем
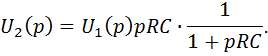
Из выражения видно, что дифференцирующая цепь является интегро-дифференцирующей, т.е. сочетает признаки интегратора и диффенциатора.
Активный дифференциатор на основе идеального ОУ
| U1 |
| K0 |
| U2 |
| R |
| С |
| I2 |
| Iс |
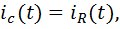
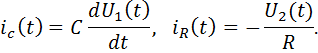
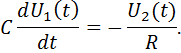
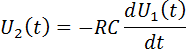
или в операторной форме
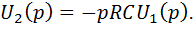
Из формулы видно, что идеальный дифференциатор осуществляет чистое дифференцирование.
Для дифференциатора на основе реального ОУ с
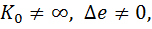 и
и 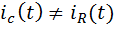
Получаем
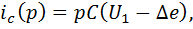
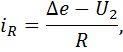
где 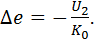
Решая систему уравнений относительно U2, окончательно получаем
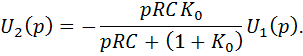
Коэффициент передачи реального активного дифференциатора с учетом 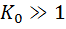 равен
равен
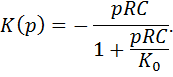
Т.е. так же присутствуют признаки интегрирования, но ослабленные в К0 раз.
Определим входное сопротивление схемы и коэффициент передачи в зависимости от частоты входного сигнала.
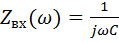 , т.е с ростом частоты входное сопротивление падает, коэффициент передачи растет
, т.е с ростом частоты входное сопротивление падает, коэффициент передачи растет
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 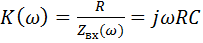 - растет.
- растет.
Схема хорошо усиливает ВЧ сигналы, а также собственные ВЧ шумы, которые искажают выходной сигнал. Кроме того на высоких частотах она может самовозбудиться из-за больших фазовых сдвигов.
На практике используют модифицированную дифференцирующую схему, в которой:
| U1 |
| K0 |
| U2 |
| С |
| R |
| Ск |
| Rвх |
- для уменьшения K(ω) на высоких частотах параллельно К включают корректирующий конденсатор Ск малой емкости.
АНАЛОГОВЫЕ ФИЛЬТРЫ
Это радиоэлектронные устройства, предназначенные для преобразования спектра сигналов.
Фильтр имеет характеристику с заранее заданным коэффициентом передачи в зависимости от частоты (АЧХ).
Фильтры классифицируются:
- по виду характеристики (по полосе пропускания, прозрачности);
| К(ω) |
| ωср |
| ω |
| 1 |
| 0,707 |
| Высокой частоты |
| К(ω) |
| ωср.н |
| ω |
| 1 |
| 0,707 |
| Режекторный (заградительный) |
| ωср.в |
| К(ω) |
| ωср.н |
| ω |
| 1 |
| 0,707 |
| Полосовой |
| ωср.в |
| К(ω) |
| ωср |
| ω |
| 1 |
| 0,707 |
| Низкой частоты |
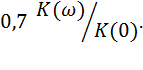 Иногда этот уровень устанавливают в размере -3дб = 0,707.
Иногда этот уровень устанавливают в размере -3дб = 0,707.
К(ω) – модуль комплексного коэффициента передачи фильтра.
Единицы измерения и масштабы отображения
Ось ординат:
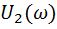 – не используется, т.к. не учитывается значение
– не используется, т.к. не учитывается значение 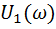 ;
;
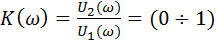 – используется при
– используется при 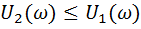 ;
;
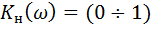 - нормированный коэффициент передачи,
- нормированный коэффициент передачи,
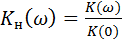 - для ФНЧ,
- для ФНЧ, 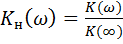 - для ФВЧ;
- для ФВЧ;
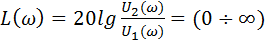 – логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
– логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
Ося абсцисс:
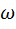 - абсолютное значение частоты, очень растянута;
- абсолютное значение частоты, очень растянута;
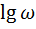 - логарифмический масштаб, сжат, компактен, но отсутствует точка
- логарифмический масштаб, сжат, компактен, но отсутствует точка 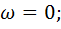
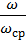 - нормированное значение относительно
- нормированное значение относительно 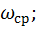
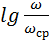 - логарифм нормированного значения частоты.
- логарифм нормированного значения частоты.
- по типу используемых электрорадиоэлементов:
LC—фильтры обладают очень хорошими характеристиками. Однако для использования их в НЧ области требуются очень большие индуктивности, что существенно увеличивает габариты изделия. Кроме того производство катушек индуктивности нетехнологично и дорого, их характеристики нестабильны во времени (эффект старения), настройки затруднены.
LC—фильтры используются на радиочастотах.
RC—фильтры широко используются в НЧ области спектра. Они компактны, стабильны во времени, достаточно легко перестраиваются, не дорогие, технологичны в производстве.
Основные характеристики фильтров
Наиболее полными характеристиками фильтров являются: амплитудно-частотная, фазо-частотная и время-частоная.
Амплитудно-частотная характеристика характеризуется:
Полоса пропускания – диапазон частот, в пределах которого ослабление сигнала фильтром составляет не более 30% или не более 3 дб или на уровне 0,707.
Плоскостность в полосе пропускания.
| К(ω) |
| 1 |
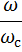
|
| 1 |
| 0,707 |
| 0,01 |
| Полоса пропускания |
| Полоса подавления |
| Склон |
| А |
| Пульсации |
Склон или спад характеристики – характеризуется крутизной или эффективностью подавления.
Полоса подавления.
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).
| L(ω) |
| 1 |
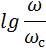
|
| 0 |
| -20 |
| -40 |
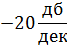
|
| 2 |
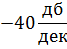
|
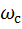 и наклоном характеристики, который определяется величиной ослабления в некотором диапазоне частот, например:
и наклоном характеристики, который определяется величиной ослабления в некотором диапазоне частот, например:
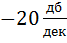 соответствует ослаблению коэффициента передачи в 10 раз в диапазоне от
соответствует ослаблению коэффициента передачи в 10 раз в диапазоне от 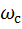 до
до 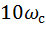 или
или
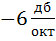 соответствует ослаблению в 2 раза в полосе от
соответствует ослаблению в 2 раза в полосе от 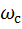 до
до 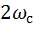 , причем:
, причем: 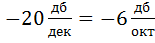 .
.
Полоса подавления начинается, когда ослабление достигнет 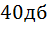 , т.е. в 100 раз.
, т.е. в 100 раз.
Фазо-частотная характеристика – показывает фазовый сдвиг гармоник выходного сигнала относительно входного и может принимать значения от 0 до 4π. От вида ФЧХ зависит степень искажения выходного сигнала на выходе фильтра – чем выше линейность, тем меньше искажения.
Время-частотная характеристика – показывает время запаздывания гармоник выходного сигнала относительно входного.
Времяимпульсная характеристика
Часто параметры фильтра задают и описывают во временной области – по оси ординат откладывают время, а не частоту. Такая характеристика называется времяимпульсной или переходной 
Её получают, подавая на вход фильтра единичный скачок
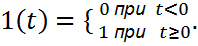
| h(t) |
| 1 |
| tн |
| t |
| 0,9 |
| 0 |
| τуст |
tн – время нарастания. Это время, необходимое для того, что бы отклик на выходе фильтра достиг уровня 0,9 от своего максимального значения;
А1 – амплитуда первого выброса и число пульсаций;
τуст – время, за которое пульсации уменьшатся до какого-то заданного значения.
Пассивные фильтры
Простейшими пассивными фильтрами являются интегрирующая и дифференцирующая RC—цепи.
1. Интегрирующая RC—цепь
| R |
| С |
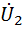
|
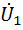
|
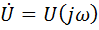
|
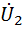
|
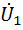
|
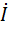
|
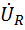
|
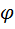
|
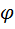
|
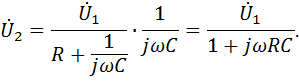
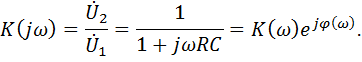
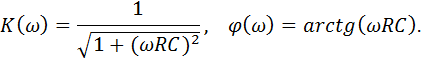
|
|
|
|
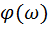
|
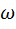
|
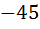
|
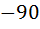
|
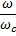
|
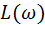
|
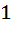
|
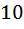
|
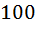
|
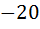
|
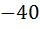
|
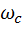
|
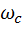
|
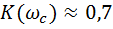
|
Построим ЛАЧХ.
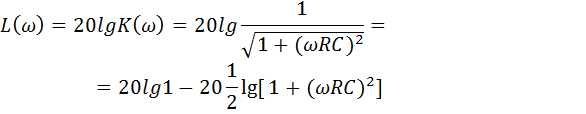
При 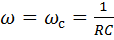 получаем
получаем 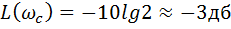 ,
,
При 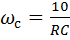 получаем
получаем 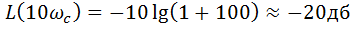 .
.
Крутизна спада составляет -20 дб/дек.
При s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>RC</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 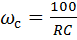
получаем 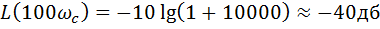 , т.е. за частотой 100ωс начинается полоса подавления.
, т.е. за частотой 100ωс начинается полоса подавления.
В операторной форме коэффициент передачи равен
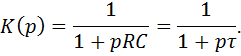
Это выражение описывает фильтр НЧ первого порядка.
2.
| R |
| С |
|
|
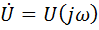
|
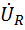
|
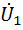
|
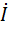
|
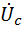
|
|
|
Дата добавления: 2017-11-04; просмотров: 836;
