Известно, что любая булева функция, отличная от нуля, может быть представлена совершенной ДНФ.
f(x1,…,xn)= 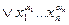
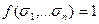
Совершенная ДНФ есть частный случай ДНФ.
К ДНФ (КНФ) можно перейти следующим образом:
1. С помощью законов де Моргана формула преобразуется к такому виду, чтобы знаки отрицания относились только к отдельным переменным;
2. На основе первого (второго) дистрибутивного закона формула сводится к дизъюнкции конъюнкций (конъюнкции дизъюнкций);
3. Полученное выражение упрощается в соответствии с тождествами
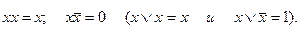
Пример.
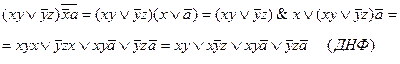
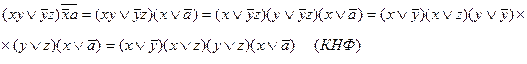
Члены Д(К)НФ, представляющие собой элементарные конъюнкции (дизъюнкции) k букв, называют минитермами (макстермами) k ранга.
Так в примере xy — минитерм второго ранга, 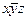 — минитерм 3-го ранга, а
— минитерм 3-го ранга, а 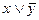 — макстерм второго ранга.
— макстерм второго ранга.
Если исходная формула содержит другие операции, то они предварительно выражаются через &, V, ù, например,
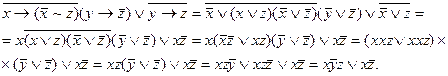
Импликантом функции f(x1,…,xn) называется элементарная конъюнкция 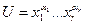 если выполнено соотношение
если выполнено соотношение
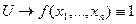 ,
,
где 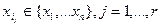 .
.
Очевидно, любая элементарная конъюнкция произвольной ДНФ, представляющей функции f(x1,…,xn), является ее импликантом, так как если эта элементарная конъюнкция на некотором наборе обращается в единицу, то функция f(x1,…,xn) тоже обращается в единицу.
Простым импликантом f(x1,…,xn) называют импликант f(x1,…,xn), если элементарная конъюнкция, получающаяся из него удалением любой буквы, не является импликантом функции.
Минимальная ДНФ f(x1,…,xn) получается из сокращенной ДНФ f(x1,…,xn) удалением некоторых элементарных конъюнкций.
Тупиковой ДНФ f(x1,…,xn) называется дизъюнкция простых импликантов, из которых ни один простой импликант нельзя удалить так, чтобы полученная ДНФ все еще представляла функцию.
Сокращенной ДНФ функции f(x1,…,xn) называется дизъюнкция всех простых импликантов функции f(x1,…,xn).
Получение минимальной ДНФ можно осуществить в два этапа. На первом этапе находят сокращенную ДНФ. На втором этапе строят тупиковые ДНФ функции, удаляя подмножества элементарных конъюнкций из сокращенной ДНФ. Из полученных тупиковых ДНФ выбирают минимальные (?).
Рассмотрим первый этап получения сокращенной ДНФ. Именно, укажем метод получения сокращенной ДНФ функции f(x1,…,xn) из СДНФ функции f(x1,…,xn) последовательным применением к ней двух равносильных преобразований:
1. Операции полного склеивания, которая состоит в замене выражения 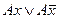 на А.
на А.
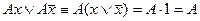
—операции неполного склеивания, которая состоит в замене выражения 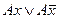 на
на 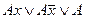 , так как
, так как
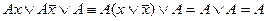 .
.
2. Операции поглощения, которая состоит в замене выражения 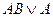 на
на 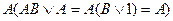 ,
,
где А и В — произвольно элементарные конъюнкции.
Минимальные формы
Любая булева функция представима в СН(Д или К) формах. Более того, такое представление является первым шагом перехода от табличного задания функций к ее аналитическому выражению.
В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получаются на основе принципа двойственности.
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний).
Такие формы называют минимальными.
Формула, представленная в ДНФ, упрощается многократным применением операции склеивания 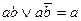 и операций поглощения
и операций поглощения 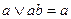 и
и 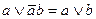 (дуальные тождества для конъюнктивной нормальной формы имеют вид:
(дуальные тождества для конъюнктивной нормальной формы имеют вид:
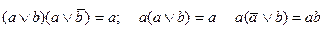 ).
).
Здесь под а и b можно понимать любую форму булевой алгебры.
В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются невозможными, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная ДНФ, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма — минимальная, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пусть, например, функция задана в СНДФ:
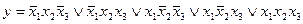
Группируя члены и применяя операцию склеивания, имеем

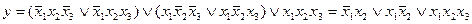 .
.
При другом способе группировки получим:
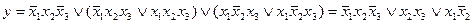 .
.
Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, т.к. 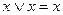 ).
).
В первом случае таким членом может быть 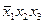 . Тогда
. Тогда
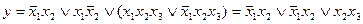 .
.
Добавляя член 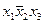 , получим:
, получим:
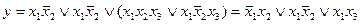 .
.
Перебрав все возможные варианты, можно убедиться, что две последние формы минимальны.
Работа на таком уровне подобна блужданию. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать графические и аналитические представления.
Дата добавления: 2017-11-04; просмотров: 515;
