Свойства средней арифметической величины
1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю.
2. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз.
3. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число.
4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится.
5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа.
2. Средняя геометрическая, средняя гармоническая,
средняя квадратическая.
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину.Ее формула такова
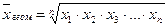 (4)
(4)
Основное применение геометрическая средняя находит при определении средних темпов роста.
Пример. В результате инфляции за первый год ценатовара возросла в 2 раза к предыдущему году, а за второй годеще в 3 раза к уровню предыдущего года. Каков средний темп роста цены за 1 год?
Решение. Согласно формуле средней геометрической (4). Среднегодовой темп роста цен равен: 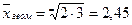 раза.
раза.
Если по условиям задачи необходимо, чтобы при осреднении неизменной оставалась сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней.
Формула простой средней гармонической величины такова:
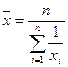 (5)
(5)
Формула взвешанной средней гармонической величины
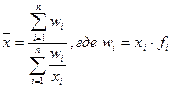 (6)
(6)
Пример.Рассчитать среднюю заработную платы по двум предприятиям, вместе: за февраль и за два месяца. Исходные данные представлены в таблице.
Таблица 4
| № предприятия | Январь | Февраль | ||
| Средняя заработная плата, руб. | Численность работников, человек | Средняя заработная плата, руб. | Фонд оплаты труда, тыс. чел. | |
Вычислить среднюю заработную плату сотрудников по двум предприятиям.
Решение.
Так исходное соотношение средней для показателя «средняя заработная плата»имеет вид
ИСС = 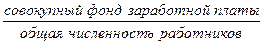 .
.
За январь средняя заработная плата рассчитана в предшествующем примере, она равна 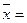 =
= 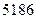 руб.,
руб.,
За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда расчет средней заработной платы в целом по двум предприятиям будет произведен по формуле средней гармонической взвешенной:
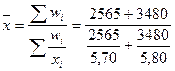 = 5757 руб.,
= 5757 руб.,
За два месяца расчет средней заработной платы по двум предприятиям произведен по формуле средней арифметической взвешанной
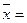
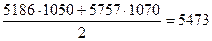 руб.,
руб.,
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Формула расчета простой квадратической средней величины:
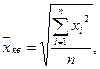 (7)
(7)
Главной сферой применения квадратической средней величины является измерение вариации признака в совокупности.
Аналогично если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической, имеющей вид:
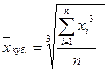 (8)
(8)
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних.
Виды степенных средних
| Вид степенной средней | Формула расчета | |
| простая | взвешенная | |
| Арифметическая | 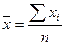
| 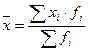
|
| Гармоническая | 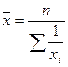
| 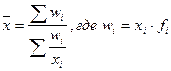
|
| Геометрическая | 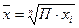
| 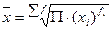
|
| Квадратическая | 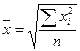
| 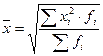
|
| Кубическая | 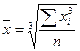
| 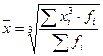
|
Правило мажорантности средних определяет связь между средними величинами:
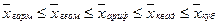 .
.
3.Структурные средние: мода, медиана
Модойназывается значение изучаемого признака, имеющего наибольшую частоту и обозначают Мо.
В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным («верблюдообразным») либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой сумму нескольких совокупностей с разными модами.
В интервальном вариационном ряду и при непрерывной вариации признака, предполагается, что каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается модой. Логично предположить, что такое значение располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала.

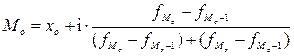 , (9)
, (9)
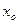 — нижняя граница модального интервала;
— нижняя граница модального интервала;
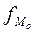 - частота в модальном интервале;
- частота в модальном интервале;
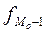 — частота интервала предшествующего модальному;
— частота интервала предшествующего модальному;
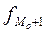 — частота интервала следующего за модальным;
— частота интервала следующего за модальным;
i — величина интервала.
Пример. Рассчитать моду по данным представленным в таблице.
Таблица 4
Распределение хозяйств области по урожайности зерновых культур
| Урожайность, ц/га, хi | Число хозяйств, fi | Середина интервала, ц/га, хi | х¢i fi | Накопленная частота, f¢i |
| 10-15 | 12,5 | 75,0 | ||
| 15-20 | 17.5 | 157,5 | ||
| 20-25 | 22,5 | 450,0 | ||
| 25-30 | 27,5 | 1127,5 | ||
| 30-35 | 32,5 | 845,0 | ||
| 35-40 | 37,5 | 787,5 | ||
| 40-45 | 42,5 | 595,0 | ||
| 45-50 | 47,5 | 237,5 | ||
| 50-55 | 52,5 | 52,5 | ||
| Итого | 4327,5 |
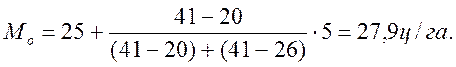
При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. Такова, например, медиана — величина варьирующего признака, делящая совокупность на две равные части по числу единиц совокупности.
Медиана не зависит от значений признака на краях ранжированного ряда. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая средняя, если ряд значений неоднороден, включает резкие отклонения от средней.
При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при 10 значениях признака — среднюю из пятого и шестого значений в ранжированном ряду.
В интервальном вариационном ряду для нахождения медианы применяется формула
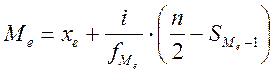 (10)
(10)
где Me — медиана;
хе — нижняя граница интервала, в котором находится медиана;
п — число наблюдений;
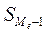 — накопленная частота в интервале, предшествующем медианному;
— накопленная частота в интервале, предшествующем медианному;
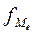 — частота в медианном интервале;
— частота в медианном интервале;
i — величина медианного интервала.
Пример. Рассчитать значение медианы по условиям предшествующей задачи.
Решение. В нашем примере имеется нечетное число значений (143+1)/2 = 72, т.е. в середине ряда находится 72-е от начала ряда значение урожайности. Как видно из ряда накопленных частот (табл. 5.4), оно находится в четвертом интервале. Тогда
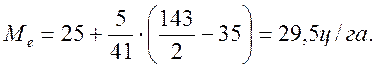
В равноинтервальном ряду медиана — это середина среднего интервала при их нечетном числе или средняя арифметическая из границ двух средних интервалов при их четном числе.
4. Квартили и децили распределения
Значения признака, делящие совокупность на четыре равные по числу единиц части, величины называются квартилями и обозначаются Q1, Q2, Q3.Значение Q2 совпадает с медианой. Для первого и третьего квартилей приводим формулы и расчет по данным таблицы (5.4)
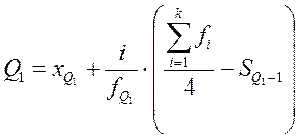 (11)
(11)
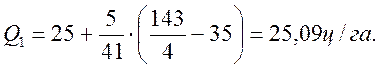
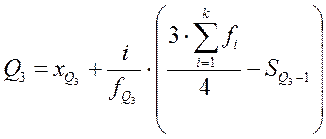 (12)
(12)
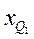 — нижняя граница интервала, в котором находится первая квартиля;
— нижняя граница интервала, в котором находится первая квартиля;
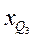 - нижняя граница интервала, в котором находится третья квартиля;
- нижняя граница интервала, в котором находится третья квартиля;
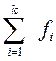 — число наблюдений;
— число наблюдений;
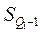 — накопленная частота в интервале, предшествующем первому квартильному;
— накопленная частота в интервале, предшествующем первому квартильному;
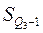 - накопленная частота в интервале, предшествующем третьему квартильному;
- накопленная частота в интервале, предшествующем третьему квартильному;
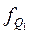 — частота в первом квартильном интервале;
— частота в первом квартильном интервале;
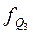 — частота в третьем квартильном интервале;
— частота в третьем квартильном интервале;
i — величина интервала.
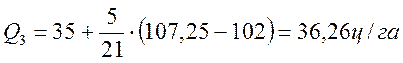
Так как Me = 29,5 ц/га, то различие между первым квартилем и медианой меньше, чем между медианой и третьим квартилем. Этот факт свидетельствует о наличии некоторой несимметричности в средней области распределения.
Значения признака, делящие ряд на пять равных частей, называют квинтилями, на десять частей — децилями, на сто частей — перцентилями.
Формула для расчета первой и девятой децили имеет вид
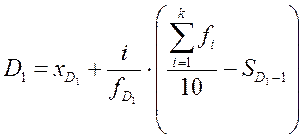 (13)
(13)
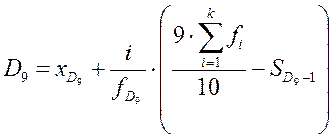 (14)
(14)
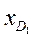 — нижняя граница интервала, в котором находится первая дециля;
— нижняя граница интервала, в котором находится первая дециля;
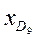 - нижняя граница интервала, в котором находится девятая дециля;
- нижняя граница интервала, в котором находится девятая дециля;
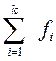 — число наблюдений;
— число наблюдений;
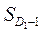 — накопленная частота в интервале, предшествующем первому децильному;
— накопленная частота в интервале, предшествующем первому децильному;
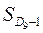 - накопленная частота в интервале, предшествующем девятому децильному;
- накопленная частота в интервале, предшествующем девятому децильному;
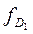 — частота в первом децильном интервале;
— частота в первом децильном интервале;
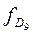 — частота в девятом децильном интервале;
— частота в девятом децильном интервале;
i — величина интервала.
Дата добавления: 2017-09-19; просмотров: 907;
