Касательная плоскость и нормаль к поверхности
Пусть имеем поверхность, заданную уравнением вида 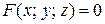 .
.
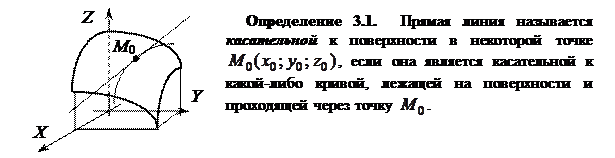
Так как через точку 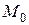 проходит бесчисленное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку будет, вообще говоря, бесчисленное множество.
проходит бесчисленное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку будет, вообще говоря, бесчисленное множество.
Введем понятие об особых и обыкновенных точках поверхности 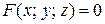 .
.
Если в точке 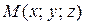 все три производные
все три производные 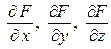 равны нулю или хотя бы одна из этих производных не существует, то точка
равны нулю или хотя бы одна из этих производных не существует, то точка 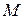 называется особой точкой поверхности. Если в точке
называется особой точкой поверхности. Если в точке 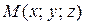 все три производные
все три производные 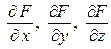 существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка
существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка 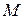 называется обыкновенной точкой поверхности.
называется обыкновенной точкой поверхности.
Теперь сформулируем теорему, которую примем без доказательства.
Теорема 3.1. Все касательные прямые к данной поверхности в ее обыкновенной точке 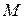 лежат в одной плоскости.
лежат в одной плоскости.
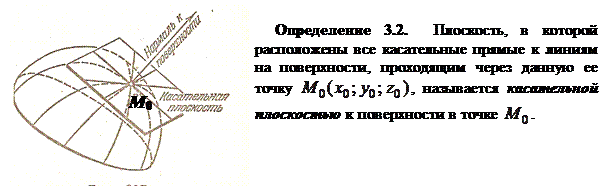
Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой. Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).
Если уравнение поверхности задано в неявном виде 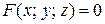 и
и 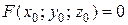 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 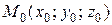 имеет вид:
имеет вид:
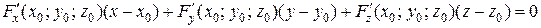 . (3.1)
. (3.1)
Если поверхность задана уравнением 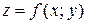 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 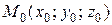 к данной поверхности имеет вид:
к данной поверхности имеет вид:
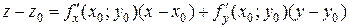 . (3.2)
. (3.2)
Определение 3.3. Прямая, проведенная через точку 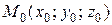 поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности.
поверхности перпендикулярно к касательной плоскости, называется нормалью к поверхности.
Если уравнение поверхности задано в неявном виде 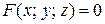 , то каноническое уравнение нормали в точке
, то каноническое уравнение нормали в точке 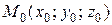 имеет вид:
имеет вид:
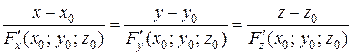 . (3.3)
. (3.3)
Если поверхность задана уравнением 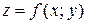 , то каноническое уравнение нормали в точке
, то каноническое уравнение нормали в точке 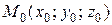 имеет вид:
имеет вид:
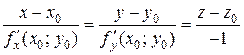 . (3.4)
. (3.4)
Пример 3.1. Найти уравнение касательной плоскости и уравнение нормали к поверхности 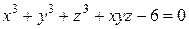 в точке
в точке 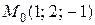
Решение. Вычисляем значения частных производных в точке 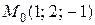 :
:
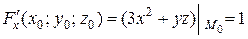 ,
,
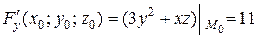 ,
,
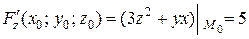 .
.
Подставляя их в уравнения (3.1) и (3.3), получаем соответственно уравнение касательной плоскости
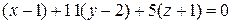 ,
,
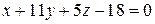
и каноническое уравнение нормали
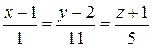 .
.
,
Дата добавления: 2017-09-19; просмотров: 1045;
