Свойства МНК-оценок

Основные предпосылки метода наименьших квадратов

Свойства оценок МНК

Найденные с помощью МНК оценки b_j параметров β_j модели линейной регрессии являются случайными величинами. Теоретически их можно представить как сумму истинного значения β_j и некоторой случайной ошибки ∆b_j (т.е. разложить на неслучайную и случайную составляющие). Для доказательства справедливости этого утверждения в формулу

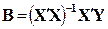
вместо вектора Y подставим его выражение: .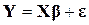

Получим:

,

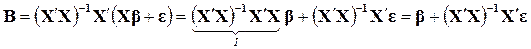где I – единичная матрица,

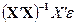= ∆b_j – вектор ошибки оценок параметров b_j.

Таким образом, свойства коэффициентов регрессии существенно зависят от свойств возмущения.

Доказано, что для получения с помощью метода наименьших квадратов наилучших результатов необходимо выполнение так называемых основных предпосылок относительно случайной составляющей (возмущения), известных как условия Гаусса-Маркова.

Предпосылки МНК

1. истинная форма взаимосвязи между зависимой переменной Y и объясняющими переменными X_j является линейной:

.

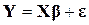2. X – неслучайная переменная. Это означает, что мы имеем фиксированный набор значений х_i.

3. Математическое ожидание случайной составляющей (возмущения) должно быть равно нулю: Е(e_i) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. Выполнимость этого условия влечет выполнимость соотношения:

.

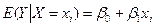4. Дисперсия возмущения e_i должна быть постоянной для всех наблюдений:

D(e_i) = s_e²для всех i.

Это так называемое условиегомоскедастичности (homoscedasticity) или равноизменчивости возмущения (зависимой переменной).

Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью (heteroscedasticity).

Поскольку

D(e_i) = Е(e_i – Е(e_i))² = Е(e_i²),

то данную предпосылку можно переписать в виде:

Е(e_i²) = s_e²для всех i.

Величина s_e² (иногда она обозначается просто s²) неизвестна (ее в регрессии оценивают с помощью остатков). Условие гомоскедастичности подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быль либо большим, либо меньшим, не должно быть априорной причины, чтобы оно порождало бо¢льшую ошибку в одних наблюдениях, чем в других.

5. Случайные составляющие e_i и e_j должны быть независимы друг от друга для i ¹ j , т.е. между ними должна отсутствовать автокорреляция.

Это условие предполагает отсутствие систематической связи между значениями возмущения в любых двух наблюдениях. Например, если возмущение велико и положительно в одном наблюдении, то это не должно обусловливать систематическую тенденцию к тому, что оно будет большим и положительным в следующем наблюдении.

Математически это условие записывается так (с учетом предпосылки 3):

Cov (e_i, e_j) = Е[(e_i – Е(e_i)(e_j – Е(e_j)] = Е(e_i e_j) = 0, i ¹ j.

6. Возмущение и независимые (объясняющие) переменные не связаны между собой. Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в данной модели.

Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайной составляющей модели равна нулю:

.

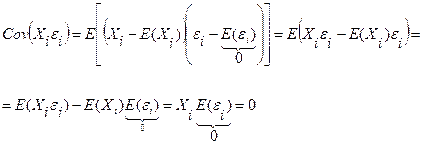7. Возмущения описываются нормальным законом распределения.

Если e нормально распределено, то и коэффициенты регрессии тоже нормально распределены. Это позволяет проводить проверку статистической надежности и определять доверительные интервалы для параметров b₀, b₁, используя t- и F- критерии.

8. В случае множественной регрессии добавляется еще одно допущение – отсутствие мультиколлинеарности между независимыми переменными, что означает невозможность представления какой-либо независимой переменной в виде линейной комбинации остальных. (Мультиколлинеарность означает наличие тесной линейной зависимости между независимыми переменными модели).

9. Модель является линейной относительно параметров.

Если выполняются основные предпосылки классической модели линейной регрессии, то оценки коэффициентов, полученные с помощью МНК, являются BLUE, что означает:

B (best) – наилучшая; L (linear) – линейная;

U (unbiased) – несмещенная; E (estimator) – оценка.

наилучшая – оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок. Теорема Гаусса – Маркова доказывает, что полученная с помощью МНК оценка является наилучшей: исследуется альтернативная произвольная линейная оценка и показывается, что ее дисперсия в любом случае окажется не меньше, чем дисперсия МНК-оценки.

Линейная – свойство линейной функциональной зависимости оценки от выборочных наблюдений.

Несмещенная – математическое ожидание оценки равно параметру генеральной совокупности.

Альтернативная формулировка желаемых свойств полученных оценок (близкая BLUE) –это требование состоятельности, несмещенности и эффективности.

Рассмотрим формулировку этих свойств.

Свойства МНК-оценок