Устойчивость линейных систем

Линейные системы обладают рядом особенностей, которые во многих случаях упрощают анализ устойчивости:

• автономная линейная система (на которую не действуют внешние силы) может иметь единственное положение равновесия (в котором все сигналы равны нулю) или бесконечно много положений равновесия (шарик на плоской поверхности);

• устойчивость – это свойство линейной системы, а не отдельного положения равновесия: или все ее движения устойчивы (асимптотически устойчивы), или все неустойчивы;

• асимптотическая устойчивость линейной системы «в малом» сразу означает ее устойчивость «в целом», то есть, при любых отклонениях от положения равновесия;

• асимптотически устойчивая система также обладает устойчивостью «вход-выход», а просто устойчивая (нейтрально устойчивая, не асимптотически устойчивая) – нет.

Для того чтобы получить условия устойчивости, рассмотрим уравнение движения линейной системы, на которую не действуют возмущения. Пусть W(s) – ее передаточная функция.

Будем считать, что она имеет только простые (не кратные) полюса 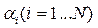(корни знаменателя)

,

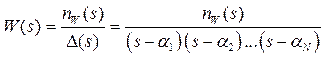где n_W(s) и Δ(s) – полиномы. Из теории линейных дифференциальных уравнений известно, что при отсутствии возмущений выход такой системы можно представить в виде

,

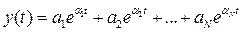где 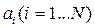– постоянные, которые определяются начальными условиями. Таким образом, процесс y(t) затухает при любых начальных условиях тогда и только тогда, когда все корни 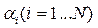имеют отрицательные вещественные части. В этом случае система асимптотически устойчива.

Поскольку устойчивость линейной системы определяют корни полинома Δ(s) – знаменателя передаточной функции W(s), этот полином называется характеристическим полиномом системы.

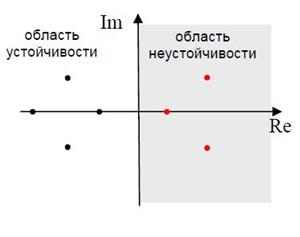
Если показать корни характеристического полинома (в общем случае – комплексные числа) на комплексной плоскости, то слева от мнимой оси будут устойчивые корни (с отрицательной вещественной частью), а справа –неустойчивые. Таким образом, область устойчивости – это левая полуплоскость.

Предположим, что один из корней полинома Δ(s) равен нулю (скажем, α₁ = 0), а остальные устойчивы, то есть, их вещественные части отрицательные. Это значит, что система содержит интегрирующее звено. Учитывая, что 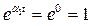при всех t, получаем

.

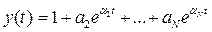Здесь все слагаемые в правой части, кроме первого, затухают с течением времени, а постоянная составляющая a₁ остается. С другой стороны, выход не возрастает неограниченно, поэтому система нейтрально устойчива.

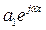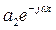Теперь допустим, что характеристический полином имеет пару чисто мнимых корней: α₁ = jω и α₂ = − jω. Это значит, что система содержит консервативные звено – генератор колебаний. При этом процесс на выходе системы содержит слагаемые и , которые могут быть (с помощью формулы Эйлера) представлены в виде

.

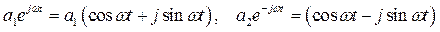Эти составляющие дают незатухающие колебания (по крайней мере, для некоторых начальных условий), поэтому система находится на границе устойчивости (нейтрально устойчива).

Переходный процесс

Хорошо спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении заданного значения выхода (уставки). Качество переходных процессов обычно оценивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал).

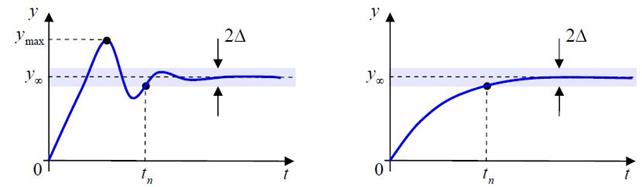
В первую очередь интересно, насколько быстро заканчивается переход на другой режим (время переходного процесса t_n). Оно определяется как время, через которое регулируемая величина «входит в коридор» шириной 2Δ вокруг установившегося значения y_∞. Это значит, что при t_n > t значение выхода отличается от установившегося не более, чем на Δ. Обычно величина Δ задается в процентах от установившегося значения, чаще всего 2% или 5%. Заметим, что для апериодического звена с постоянной времени T время переходного процесса равно t_п = 3T (с точностью 5%).

Другая важная характеристика – перерегулированиеσ – показывает, на сколько процентов максимальное значение выхода y_max превышает установившееся значение y_∞

.

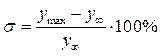Иногда удается обеспечить нулевое перерегулирование (апериодический переходный процесс, как у апериодического звена). Нужно помнить, что увеличение быстродействия обычно приводит к увеличению перерегулирования.

Устойчивость линейной системы определяется полюсами ее передаточной функции W(s), однако на переходные процесс влияют и нули, причем в некоторых случаях очень существенно. Для примера рассмотрим передаточную функцию

,

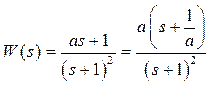где a может принимать как положительные, так и отрицательные значения. Такая передаточная функция имеет нуль в точке s = −1/ a. Нули, находящиеся в левой полуплоскости (при a > 0) часто называют устойчивыми (по аналогии с полюсами), а нули в правой полуплоскости (при a < 0) – неустойчивыми. Очевидно, что при a = 0 мы получаем апериодическое звено второго порядка. Теперь построим переходные характеристики этого звена при разных значениях a. Заметим, что при любом a установившееся значение выхода равно W(0) = 1.

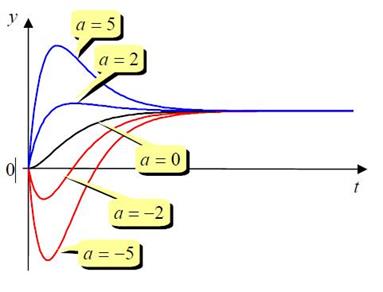
По графикам видно, что при нулевом значении a переходный процесс – апериодический. При a > 0 (устойчивый нуль) наблюдается перерегулирование, причем оно тем больше, чем больше модуль a. При отрицательных значениях a в переходном процессе есть недорегулирование. Это значит, что в первый момент времени регулируемая переменная начинает изменяться в сторону, противоположную заданному значению.

Робастность

Обычно регулятор строится на основе некоторых приближенных (номинальных) моделей объекта управления (а также приводов и датчиков) и внешних возмущений. При этом поведение реального объекта и характеристики возмущений могут быть несколько иными. Поэтому требуется, чтобы разработанный регулятор обеспечивал устойчивость и приемлемое качество системы при малых отклонениях свойств объекта и внешних возмущений от номинальных моделей. В современной теории управления это свойство называют робастностью (грубостью).

Иначе его можно назвать нечувствительностью к малым ошибкам моделирования объекта и возмущений.

Различают несколько задач, связанных с робастностью

• робастная устойчивость– обеспечить устойчивость системы при всех допустимых отклонениях модели объекта от номинальной;

• робастное качество– обеспечить устойчивость и заданные показатели качества системы при всех допустимых отклонениях модели объекта от номинальной;

• гарантирующее управление– обеспечить заданные показатели качества системы при всех допустимых отклонениях модели возмущения от номинальной (считая, что модель объекта известна точно).

Для того, чтобы исследовать робастность системы, нужно как-то определить возможную ошибку моделирования (неопределенность).