Оценка постоянного аннуитета постнумерандо.
Аннуитет называется постоянным (fixed annuity), если все денежные поступления равны между собой. В этом случае 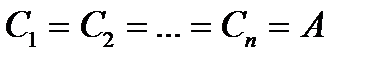
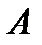 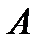 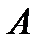 ... ... 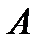 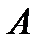 0 1 2 ...
0 1 2 ... 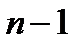 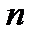
|
| Аннуитет пренумерандо Аннуитет постнумерандо |
  ... ...   0 1 2 ...
0 1 2 ... 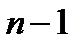 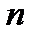
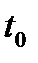 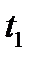 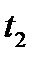 ... ... 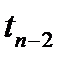 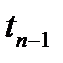 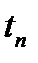
|
Рис. 7. Виды постоянных аннуитетов
Прямая задача оценки срочного аннуитета при заданных величинах регулярного поступления 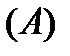 и процентной ставке
и процентной ставке 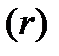 предполагает оценку будущей стоимости аннуитета
предполагает оценку будущей стоимости аннуитета 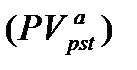 . Как следует из логики, присущей схеме аннуитета, записанный в порядке поступления платежей наращенный денежный поток (в аннуитете постнумерандо) имеет вид:
. Как следует из логики, присущей схеме аннуитета, записанный в порядке поступления платежей наращенный денежный поток (в аннуитете постнумерандо) имеет вид:
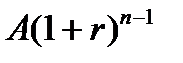 ,
, 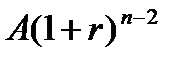 ,…,
,…, 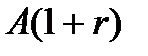 ,
, 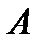 ,
,
а формула (7.1) трансформируется следующим образом:
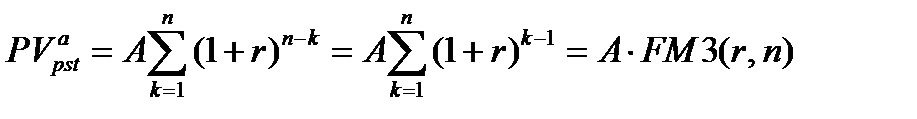 (7.7)
(7.7)
Входящий в формулу множитель 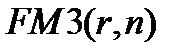 называется коэффициентом наращения ренты (аннуитета) и представляет собой сумму
называется коэффициентом наращения ренты (аннуитета) и представляет собой сумму 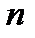 первых членов геометрической прогрессии, начинающейся (в обозначениях первого раздела) с
первых членов геометрической прогрессии, начинающейся (в обозначениях первого раздела) с 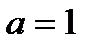 и имеющей знаменатель
и имеющей знаменатель 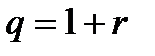 .
.
Таким образом,
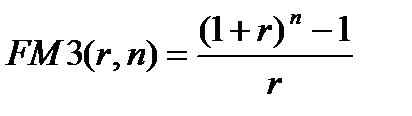 (7.8)
(7.8)
Из (7.8) следует, что
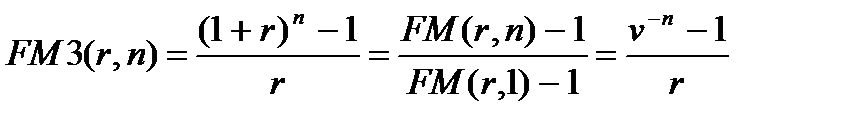 .
.
Экономический смысл множителя 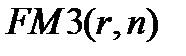 заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель
заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель 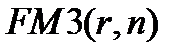 часто используется в финансовых вычислениях. Его значения зависят лишь от процентной ставки
часто используется в финансовых вычислениях. Его значения зависят лишь от процентной ставки 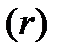 и срока
и срока 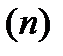 действия аннуитета, причем с увеличением каждого из этих параметров величина
действия аннуитета, причем с увеличением каждого из этих параметров величина 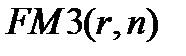 возрастает. Значения множителя для различных сочетаний
возрастает. Значения множителя для различных сочетаний 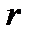 и
и 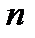 можно табулировать. Заметим, что при выводе формулы (7.7) использовали выражение процентной ставки
можно табулировать. Заметим, что при выводе формулы (7.7) использовали выражение процентной ставки 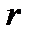 в десятичных дробях.
в десятичных дробях.
Из (7.7) следует, что 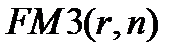 показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления
показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления 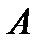 . В связи с этим множитель
. В связи с этим множитель 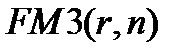 называют также коэффициентом аккумуляции вкладов.
называют также коэффициентом аккумуляции вкладов.
В формуле (7.7) переменная 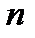 означает число периодов, а
означает число периодов, а 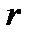 представляет собой ставку за период. И период, конечно, не обязательно должен быть равен одному году. Так, если в качестве периода понимать один квартал, то
представляет собой ставку за период. И период, конечно, не обязательно должен быть равен одному году. Так, если в качестве периода понимать один квартал, то 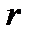 является сложной ставкой за один квартал.
является сложной ставкой за один квартал.
Коэффициент наращения ренты 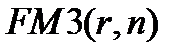 обладает рядом свойств, которые можно получить математически и которые имеют содержательную финансовую интерпретацию. Например, для любого целого
обладает рядом свойств, которые можно получить математически и которые имеют содержательную финансовую интерпретацию. Например, для любого целого 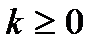 справедливо равенство
справедливо равенство
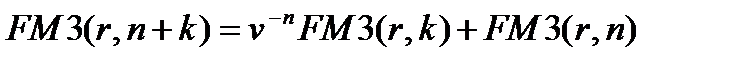 (7.9)
(7.9)
Если 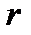 является процентной ставкой (в десятичных дробях) за базовый период, а начисление сложных процентов происходит
является процентной ставкой (в десятичных дробях) за базовый период, а начисление сложных процентов происходит 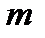 раз в течение этого периода (не пишем
раз в течение этого периода (не пишем 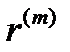 , поскольку период в принципе"может отличаться от года), то наращенный денежный поток, начиная с последнего денежного поступления, имеет вид
, поскольку период в принципе"может отличаться от года), то наращенный денежный поток, начиная с последнего денежного поступления, имеет вид
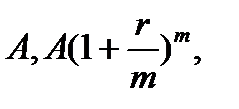
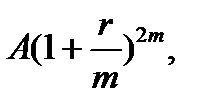 …,
…, 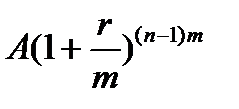
Другими словами, получили геометрическую прогрессию,
первый член которой равен 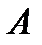 и знаменатель -
и знаменатель - 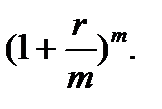 Следовательно, сумма
Следовательно, сумма 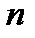 первых членов этой прогрессии равна:
первых членов этой прогрессии равна:
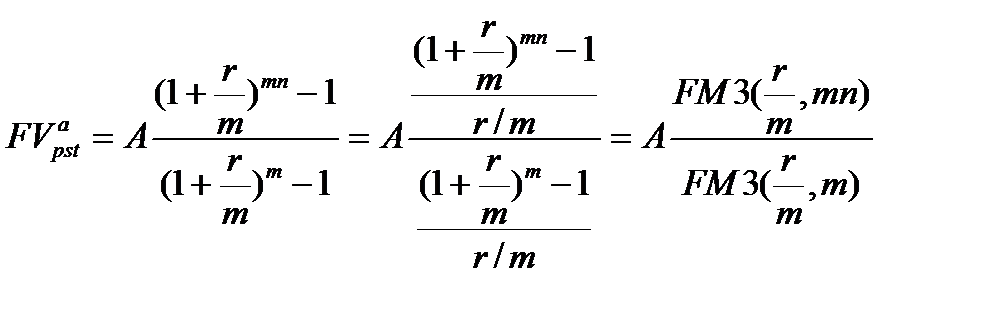 (7.11)
(7.11)
Ситуацию, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода, можно рассматривать с двух точек зрения. Изложим первую из них.
Пусть в течение базового периода денежные поступления происходят 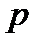 раз и один раз в конце периода начисляются проценты в соответствии со ставкой
раз и один раз в конце периода начисляются проценты в соответствии со ставкой 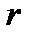 .
.
Определим сумму, которая накопится к концу любого периода, если на отдельные взносы, поступающие в течение периода, начисляются сложные проценты.
На последнее 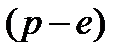 поступление проценты не начисляются и оно остается равным
поступление проценты не начисляются и оно остается равным 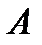 . На предпоследнее
. На предпоследнее 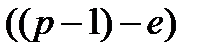 поступление начисляются сложные проценты за
поступление начисляются сложные проценты за 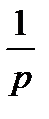 -ю часть периода и оно будет равно
-ю часть периода и оно будет равно 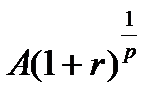 . На
. На 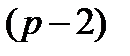 -е поступление начисляются сложные проценты за
-е поступление начисляются сложные проценты за 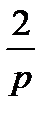 -ю часть периода и оно будет равно
-ю часть периода и оно будет равно 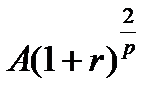 и т.д. до первого включительно, которое будет равно
и т.д. до первого включительно, которое будет равно 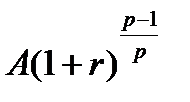 . Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем
. Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем 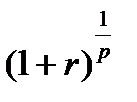 и числом членов, равным
и числом членов, равным 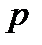 , поэтому сумма этих величин равна:
, поэтому сумма этих величин равна:
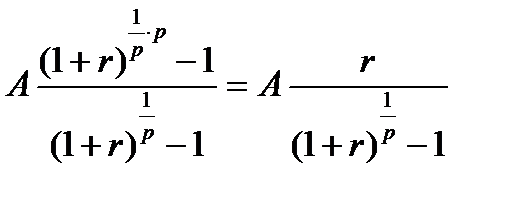
Таким образом, можно считать, что имеем аннуитет, в котором денежные поступления равны величине 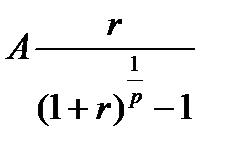 и происходят в конце каждого базового периода начисления процентов. Поэтому, пользуясь (7.7), получим:
и происходят в конце каждого базового периода начисления процентов. Поэтому, пользуясь (7.7), получим:
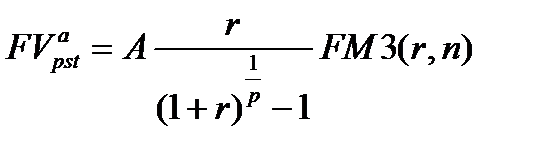
А учитывая (7.8), можно написать
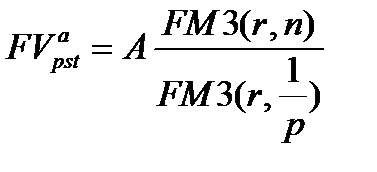 (7.12)
(7.12)
Аналогичным образом можно рассмотреть и самую общую ситуацию, когда в течение базового периода денежные поступления происходят 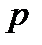 раз и проценты начисляются
раз и проценты начисляются 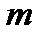 раз за период. Например, если начисляются только сложные проценты, то, как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода. Последнее
раз за период. Например, если начисляются только сложные проценты, то, как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода. Последнее 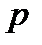 -е поступление в периоде остается равным А. Предпоследнее
-е поступление в периоде остается равным А. Предпоследнее 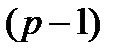 -e поступление после начисления сложных процентов составит
-e поступление после начисления сложных процентов составит 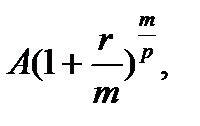
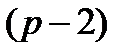 -е поступление -
-е поступление - 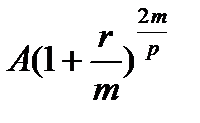 и т.д. до первого, которое станет равным
и т.д. до первого, которое станет равным 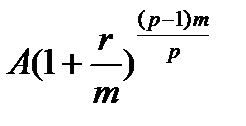 . Находим сумму полученных величин:
. Находим сумму полученных величин:
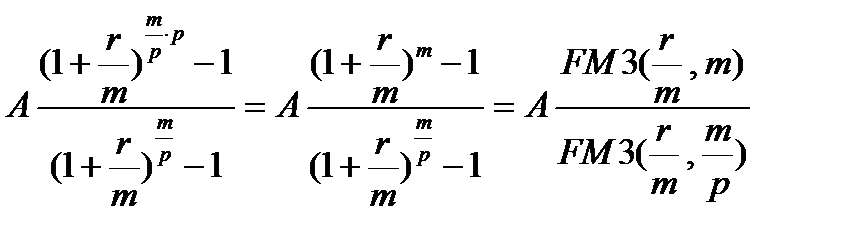 .
.
Считая, что есть аннуитет с денежными поступлениями, равными полученной сумме, воспользуемся формулой (7.11):
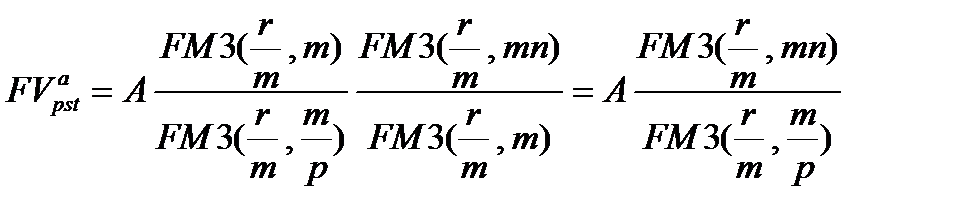 (7.14)
(7.14)
Заметим, что при начислении на отдельные поступления внутри периода простых процентов (согласно их свойству) для 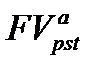 и в этом случае получим опять формулу (7.13).
и в этом случае получим опять формулу (7.13).
Преобразуем формулу (7.14), предполагая, что длительность базового периода начисления процентов равна одному году, и используя понятие эффективной годовой процентной ставки 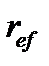 .
.
Так как 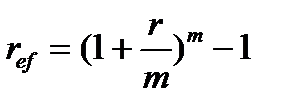 , то
, то
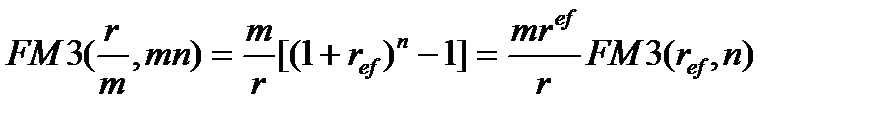
Пользуясь этими соотношениями, получим:
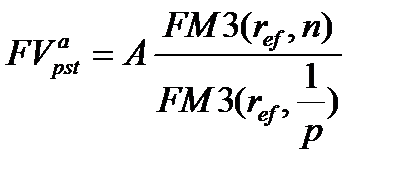 (7.15)
(7.15)
Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо 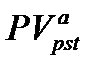 выводится из основной формулы (7.3) и имеет вид:
выводится из основной формулы (7.3) и имеет вид:
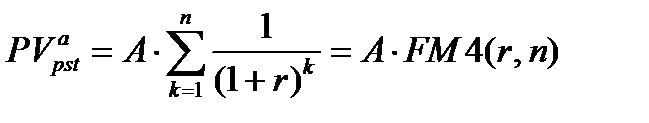 (7.16)
(7.16)
Множитель 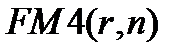 называется коэффициентом дисконтирования ренты (аннуитета) и как сумма членов геометрической прогрессии равен величине:
называется коэффициентом дисконтирования ренты (аннуитета) и как сумма членов геометрической прогрессии равен величине:
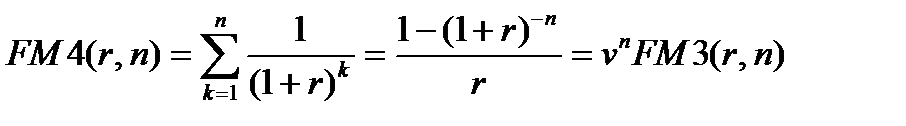 (7.17)
(7.17)
Экономический смысл дисконтного множителя 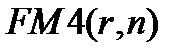 заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающегося
заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающегося 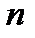 равных периодов с заданной процентной ставкой
равных периодов с заданной процентной ставкой 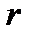 . Значения этого множителя также табулированы и, как для других множителей, процентная ставка
. Значения этого множителя также табулированы и, как для других множителей, процентная ставка 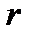 дана в процентах.
дана в процентах.
Дисконтный множитель 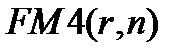 полезно интерпретировать и как величину капитала, поместив который в банк под сложную процентную ставку г, можно обеспечить регулярные выплаты в размере одной денежной единицы в течение
полезно интерпретировать и как величину капитала, поместив который в банк под сложную процентную ставку г, можно обеспечить регулярные выплаты в размере одной денежной единицы в течение 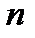 периодов (выплаты производятся в конце каждого периода). Действительно, к концу первого периода величина
периодов (выплаты производятся в конце каждого периода). Действительно, к концу первого периода величина 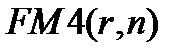 станет равной:
станет равной:
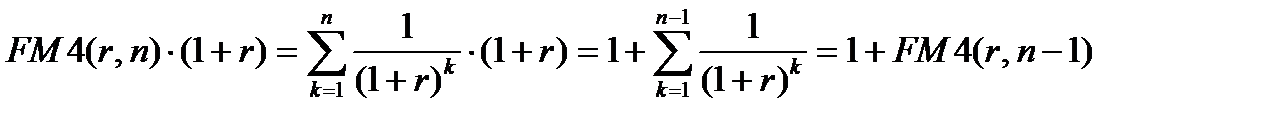
В конце первого периода одна денежная единица будет выплачена и останется капитал 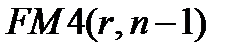 , который в конце второго периода станет равным:
, который в конце второго периода станет равным:
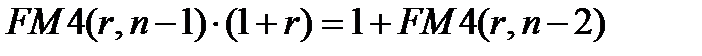
После выплаты денежной единицы останется капитал 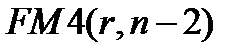 . Продолжая рассуждения аналогичным образом, убеждаемся, что в конце
. Продолжая рассуждения аналогичным образом, убеждаемся, что в конце 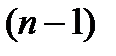 -ro периода будем иметь капитал, равный:
-ro периода будем иметь капитал, равный:
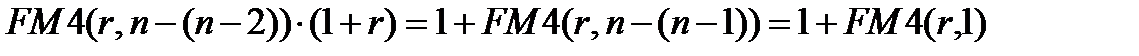
После выплаты одной денежной единицы капитал 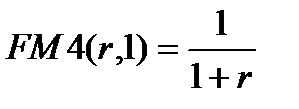 , очевидно, обеспечит выплату последней денежной единицы в конце
, очевидно, обеспечит выплату последней денежной единицы в конце 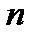 -го периода.
-го периода.
Например, поскольку 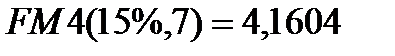 , то, поместив 4 тенге 16 тиын под сложную процентную ставку 15%, можно обеспечить выплаты по 1 тенге в конце каждого года в течение 7 лет.
, то, поместив 4 тенге 16 тиын под сложную процентную ставку 15%, можно обеспечить выплаты по 1 тенге в конце каждого года в течение 7 лет.
Из вида выражения (7.17) следует, что при возрастании процентной ставки 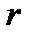 величина дисконтного множителя
величина дисконтного множителя 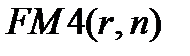 уменьшается и, таким образом, уменьшается величина приведенной (текущей) стоимости.
уменьшается и, таким образом, уменьшается величина приведенной (текущей) стоимости.
В формуле (7.16), как и в формуле (7.7), переменная 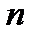 означает число периодов, которые необязательно равны году, что позволяет при соответствующем понимании ставки
означает число периодов, которые необязательно равны году, что позволяет при соответствующем понимании ставки 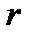 пользоваться этой формулой в различных ситуациях.
пользоваться этой формулой в различных ситуациях.
Коэффициент дисконтирования ренты 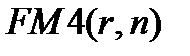 удовлетворяет соотношениям, подобным (7.9) и (7.10). Равенства для
удовлетворяет соотношениям, подобным (7.9) и (7.10). Равенства для 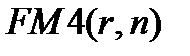 можно вывести аналогичным образом, как и для
можно вывести аналогичным образом, как и для 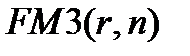 . Укажем еще один на первый взгляд формальный математический прием, тем не менее отражающий финансовый подход. Из (7.17) следует, что
. Укажем еще один на первый взгляд формальный математический прием, тем не менее отражающий финансовый подход. Из (7.17) следует, что 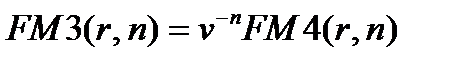 . Подставляя это выражение в (7.9) и (7.10), получим
. Подставляя это выражение в (7.9) и (7.10), получим
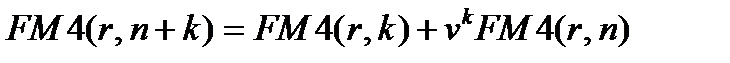 (7.18)
(7.18)
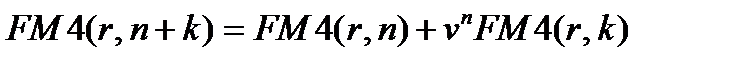 (7.19)
(7.19)
Эти соотношения, как и (7.9), (7.10), имеют простой финансовый смысл. Например, равенство (7.18) означает, что приведенную стоимость срочного аннуитета в одну денежную единицу со сроком действия 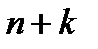 можно найти путем сложения приведенной стоимости аннуитета за первые к периодов и учтенной за время к приведенной стоимости (на момент начала
можно найти путем сложения приведенной стоимости аннуитета за первые к периодов и учтенной за время к приведенной стоимости (на момент начала 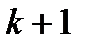 -го периода) аннуитета за оставшиеся
-го периода) аннуитета за оставшиеся 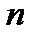 периодов.
периодов.
Из формулы (7.17) следует, что
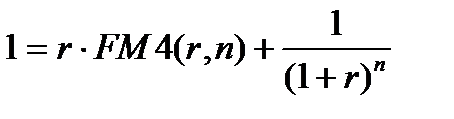 ,
,
или используя обозначение дисконтного множителя,
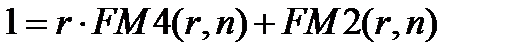
Это равенство можно пояснить, например, таким образом: долг в одну денежную единицу можно погасить равными платежами в 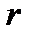 денежных единиц в конце периодов от 1 до
денежных единиц в конце периодов от 1 до 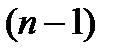 -го, а в конце
-го, а в конце 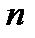 -го периода необходимо выплатить
-го периода необходимо выплатить 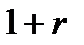 денежных единиц.
денежных единиц.
Вообще в случае рассмотрения только сложных процентов выводы формул для нахождения приведенных стоимостей аннуитетов аналогичны выводам формул для нахождения наращенных сумм. Получающиеся при рассуждениях денежные потоки будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители. Так, для постоянного аннуитета постнумерандо с начислением сложных процентов 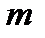 раз за базовый период приведенный денежный поток имеет вид
раз за базовый период приведенный денежный поток имеет вид
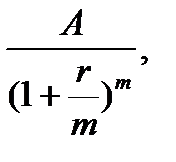
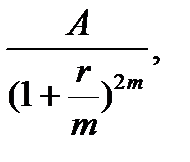 …,
…, 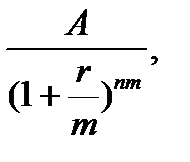
следовательно, сумма этих величин (приведенная стоимость аннуитета) равна:
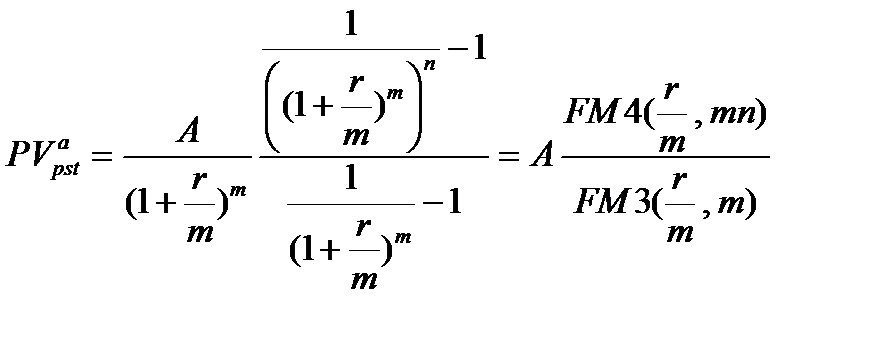 (7.20)
(7.20)
Для 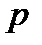 -срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и т раз за базовый период можно получить
-срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и т раз за базовый период можно получить
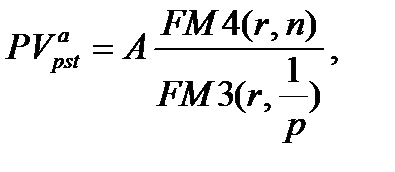 (7.21)
(7.21)
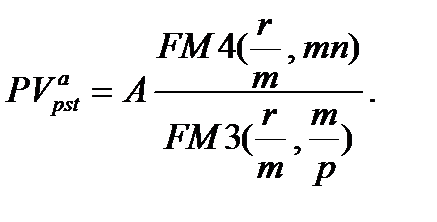 (7.22)
(7.22)
Как видно, формулы (7.20) - (7.22) похожи соответственно на формулы (7.11), (7.12), (7.14). Применяя эффективную годовую процентную ставку 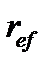 , получим:
, получим:
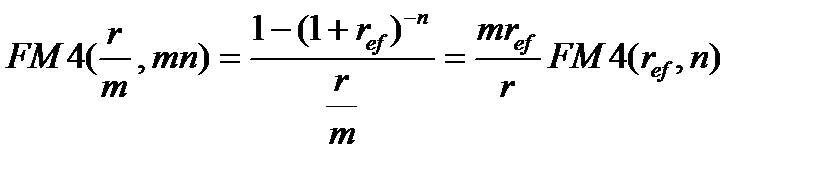
Поэтому из (7.22) следует, что
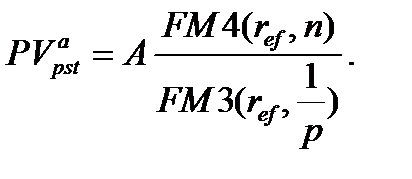 (7.23)
(7.23)
Соотношение (7.23) по виду совпадает с (7.21), что объясняется содержанием понятия эффективной ставки.
Дата добавления: 2017-05-18; просмотров: 1244;
