Сравнительный анализ структур

При выборе структуры для представления конкретной системы следует учитывать их особенности и возможности.

Сетевые структуры используются в тех случаях, когда систему удаётся отобразить через описание материальных и информационных процессов, происходящих в ней, т.е. представить последовательностью изготовления изделий, прохождения документов и т.д.

Предпочтительно представление во времени для процессов проектирования новых систем. Однако такое представление практически невозможно для сложных технических комплексов, особенно при проектировании организационных систем управления. В этих случаях вначале используют расчленение системы в пространстве, т.е. представление её различными видами иерархических структур.

Наиболее предпочтительно получение древовидной структуры, которая более чётко отражает взаимоотношения между компонентами системы. Такое представление предпочтительно при организации производства сложных технических комплексов: древовидное расчленение изделия позволяет определить основные структурные единицы

(цехи, участки и т.п.) производственной структуры, уточнение взаимодействия между которыми затем ведётся с помощью сетевых структур.

В организационных системах взаимоотношения между структурными единицами организационной структуры гораздо более сложны. Их не всегда удаётся сразу отобразить с помощью древовидной структуры. Используются иерархии со «слабыми связями», матричные структуры, а для сложных корпораций – многоуровневые структуры типа страт, эшелонов, смешанные структуры с вертикальными и горизонтальными связями.

От вида структур зависит важная характеристика любой системы – степень её целостности, устойчивости.

Для сравнительного анализа структур используются информационные оценки степени целостности α и коэффициента использования компонентов системы β, которые могут интерпретироваться как оценки устойчивости оргструктуры при предоставлении свободы элементам или как оценки степени централизации-децентрализации управления в системе.

Эти оценки получены из соотношения, определяющего взаимосвязь системной Сс, собственной Со и взаимной Св сложности системы:

Сс= Со + Св. (1.10)

Собственная сложность Со представляет собой суммарную сложность (содержание) элементов системы вне связи их между собой (в случае прагматической информации – суммарную сложность элементов, влияющих на достижение цели).

Системная сложность Сс характеризует содержание системы как целого (например, сложность её использования).

Взаимная сложность Св характеризует степень взаимосвязи элементов в системе (т.е. сложность её устройства, схемы, структуры).

Разделив члены выражения (1.10) на Со, получим две важные сопряжённые оценки:

α = – Св / Со ; (1.11)

β = Сс / Со , (1.12)

причём β = 1 – α.

Оценка (1.11) характеризует степень целостности, связности, взаимозависимости элементов системы; для организационных систем α может быть интерпретирована как характеристика устойчивости, управляемости, степени централизации управления.

Оценка (1.12) показывает самостоятельность, автономность частей в целом, степень использования возможностей элементов. Для организационных систем β удобно называть коэффициентом использования элементов в системе.

Знак минус в выражении (1.11) введён для того, чтобы α было положительным, поскольку Св в устойчивых системах, для которых характерно Со > Сс, формально имеет отрицательный знак. Связанное (остающееся как бы внутри системы) содержание Св характеризует работу системы на себя, а не на выполнение стоящей перед ней цели (чем и объясняется отрицательный знак Св).

Последнее особенно важно учитывать при формировании оргструктур предприятий и других организаций.

Модели систем

Наиболее простое определение системы – это средство достижения цели, а цель – это субъективный абстрактный образ ещё не существующего, но желаемого состояния среды или окружающего нас мира.

Анализируя системы, легко показать, что цели систем могут быть неоднозначными, что одну и ту же систему можно использовать для разных целей.

Сформулировать цель даже существующих систем сложно, тем более сформулировать цель проектирования систем. Поэтому для решения задачи создания системы следует совершенствовать и развивать её модель.

Наиболее простой моделью является модель «чёрного ящика» 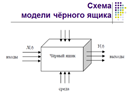. Идея использования «чёрного ящика» возникла от недостаточности знания внутреннего строения (состава) самой системы, поэтому её мы изображаем в виде непрозрачного ящика, который обладает следующими свойствами: целостность и его обособленность от среды.

Второе свойство говорит о том, что ящик выделен из среды, но не является полностью изолированным, т.е. ящик (система) связан со средой связями. Среда воздействует на него, и он действует на среду.

Наряду с очевидностью модели «чёрного ящика» его простота обманчива. При описании любой реальной системы очень часто мы сталкиваемся с трудностями в определении всех входов и выходов этой системы. Неучёт существенных входных или выходных параметров системы приводит часто к недостижению поставленной цели.

Выбор входов «чёрного ящика» является противоположной задачей. Использование модели «чёрного ящика» даёт те результаты, которые определяются целью системы.

3.1. Модель состава системы

Очевидно, что модель чёрного ящика не рассматривает внутреннее устройство системы, поэтому для моделирования и детализации описания состава системы требуется усложнение модели, т.е. создание модели состава системы (рис.2.5).

Данная модель описывает основные составные части системы, рассматривает элементы системы как неделимые части и подсистемы, т.е. модель состава иллюстрирует иерархию составных частей системы.

На первый взгляд, эта модель кажется простой, но если дать задание экспертам определить состав одной и той же системы, то у каждого эксперта будет своя модель, отличающаяся от моделей других. Это объясняется тем, что, во-первых, понятие элемента у всех будет разным. Во-вторых, поскольку модель состава является деловой, то для различных целей требуются различные составные части этой системы и, в-третьих, деление всей системы над подсистемы является относительным или условным, так как границы этих подсистем, число этих подсистем и их состав будут различными, а значит и модели будут разными.

3.2. Модель структуры системы

Для достижения многих практических целей недостаточно моделей «чёрного ящика» или модели состава, необходимо ещё правильно соединить все элементы между собой, т.е. установить или определить отношения между элементами.

Совокупность необходимых и достаточных для достижения целей отношений между элементами называется структурой системы.

Бесконечность природы любой системы порождает невообразимое количество этих отношений. Однако при построении системы мы рассматриваем некоторую совокупность важных отношений.

В отношении участвует не менее двух объектов, а свойством мы называем некоторый атрибут только одного объекта, поэтому свойства есть частный случай отношения или следствие отношений между объектами.

Отсюда появилось второе определение, более глубокое, системы – это совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.

В этом случае модель охватывает «чёрный ящик», модель состава и модель структуры. Вместе они образуют ещё одну модель, которая называется структурной схемой системы.

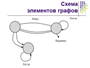Часто структурная схема описывается с помощью математической модели. Однако в настоящее время системы описываются с помощью схемы, состоящей из элементов и связей между ними. Такая схема называется графом (рис. 2.6).

В графах элементы называются вершинами, а связи между ними называются ребрами, и вершины обозначаются кружками, а связи – в виде линий. Если не указаны направления связи, то такой граф называется неориентированным.

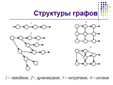Вершины могут соединяться между собой любым количеством рёбер (линий), и вершина может быть связана сама с собой, тогда ребро называется петлёй.

Если связи между вершинами имеют размерную природу, то они обозначаются разными линиями и имеют различные веса, а графы называются взвешенными.

Теория графов имеет многочисленные приложения.

Особое место в теории систем занимают (системы) структуры с обратными связями, которые соответствуют кольцевым путям в ориентированных графах.

Часто структура информации, содержащаяся в графах, для ряда исследований недостаточна, поэтому методы теории графов становятся вспомогательными, а главными являются функциональные связи между входами и выходами или внутренними связями системы (рис. 2.7).

В реальности системы, а именно их структура и взаимосвязи меняются во времени, и такие системы называются динамическими. Поэтому всегда для описания реальных систем требуется создавать модели, которые описывают динамику изменения системы (в русском языке «динамический» означает – изменяющийся) и использование функциональных моделей, отражающих вид связи и его изменение во времени, является наиболее адекватной моделью описания любых объектов.

Все динамические системы бывают линейными и нелинейными. Нелинейные – зависящие от многих параметров.