Абсолютные и средние показатели вариации
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.
Размах колебаний (размах вариации) – это разность между наибольшим ( 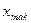 ) и наименьшим (
) и наименьшим ( 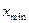 ) значениями вариантов
) значениями вариантов
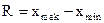
Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями.
Точнее характеризует вариацию признака показатель, основанный на учете колеблемости всех значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений признака отдельных единиц совокупности от этой величины. К таким показателям относятся среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, представляющие собой среднюю арифметическую из отклонений индивидуальных значений признака от средней арифметической. Среднее линейное отклонение рассчитывается из отклонений в первой степени, дисперсия и среднее квадратическое - из отклонений во второй степени. Так как алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической (согласно нулевому свойству) всегда равна нулю, то для расчета среднего линейного отклонения используется арифметическая сумма отклонений, т.е. суммируются абсолютные значения индивидуальных отклонений значений признака независимо от знака.
Среднее линейное отклонение вычисляется по следующим формулам:
aдля несгруппированных данных
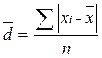 |
aдля сгруппированных данных (вариационного ряда)
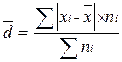 |
Порядок расчета среднего линейного отклонения простого следующий:
1) по значениям признака исчисляется средняя арифметическая:
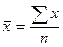 ;
;
2) определяются отклонения каждой варианты 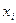 от средней
от средней 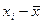 ;
;
3) рассчитывается сумма абсолютных величин отклонений: 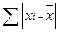 ;
;
4) сумма абсолютных величин отклонений делится на число значений
Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная:
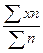 ;
;
2) определяются абсолютные отклонения вариант от средней 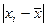 ;
;
3) полученные отклонения умножаются на частоты 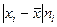 ;
;
4) находится сумма взвешенных отклонений без учета знака:
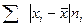 ;
;
5) сумма взвешенных отклонений делится на сумму частот:
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается 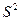 . В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
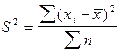 — дисперсия невзвешенная (простая);
— дисперсия невзвешенная (простая);
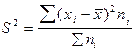 — дисперсия взвешенная.
— дисперсия взвешенная.
Дисперсия имеет большое значение в статистическом анализе. Однако её применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. В таких случаях для измерения вариации признака вычисляют среднее квадратическое отклонение.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
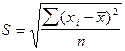 — среднее квадратическое отклонение невзвешенное;
— среднее квадратическое отклонение невзвешенное;
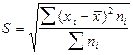 — среднее квадратическое отклонение взвешенное.
— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенную:
1) определяют среднюю арифметическую взвешенную
2) определяются отклонения вариант от средней 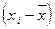 ;
;
3) возводят в квадрат отклонение каждой варианты от средней 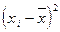 ;
;
4) умножают квадраты отклонений на веса (частоты) 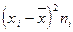 ;
;
5) суммируют полученные произведения
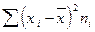 ;
;
6) Полученную сумму делят на сумму весов
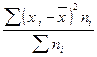 .
.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее применить тот же метод, что изложен выше.
Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Основные свойства дисперсии.
Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в 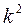 раз, а среднее квадратическое отклонение - в к раз.
раз, а среднее квадратическое отклонение - в к раз.
Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: 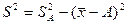 . Если А равна нулю, то приходим к следующему равенству:
. Если А равна нулю, то приходим к следующему равенству: 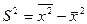 , т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую 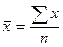 ;
;
2) возводят в квадрат среднюю арифметическую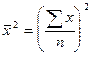 ;
;
3) возводят в квадрат каждую варианту ряда 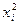 ;
;
4) находим сумму квадратов вариант 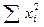 ;
;
5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат 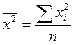 ;
;
6) определяют разность между средним квадратом признака и квадратом средней 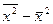 .
.
Дата добавления: 2017-04-20; просмотров: 919;
