Примеры антирефлексивных отношений
· отношение неравенства
· отношения строгого порядка:
o отношение строгого неравенства
o отношение строгого подмножества
· отношение перпендикулярности прямых (или ортогональности ненулевых векторов) в геометрии.
19. Симметричность бинарного отношения. Пример.
Симметричность: для любых двух элементов а, b є М : аRb и bRа (т.е. R = R-1). Симметрична параллельность прямых, так как если a II b, то
b II a («быть равным»; «быть взаимнопростым»).
Симметричность. Отношение Q называется симметричным, если для любой пары <a, b>ÎA2 при выполнении aQb выполняется и bQa. Например, на множестве людей симметричными являются отношения «быть родственником», «быть похожим».
20. Антисимметричные бинарные отношения. Пример.
Aнтисимметричность: если для а ≠ b верно отношение аRb, то ложно bRа («быть больше», «не меньше», «быть делителем»).
R = {(x,y) : x є R, у є R, х-у ≥ 1} обладает свойствами антисимметрич-ности
21. Транзитивные бинарные отношения. Пример.
Транзитивность: если аRb и bRс, то аRс для любых а, b, с є М («быть больше», «быть параллельным», «быть равным»).
R = {(x,y) : x є R, у є R, х-у ≥ 1}
22. Отношение эквивалентности. Пример.
Бинарное отношение a на множестве X называется отношением эквивалентности на X, если a рефлексивно, симметрично и транзитивно.
Отношение эквивалентности часто обозначают символами ~, 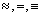 .
.
Примерами отношения эквивалентности служат:
· отношение тождества IX = {(a, a)|a 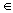 X} на непустом множестве X;
X} на непустом множестве X;
· отношение параллельности на множестве прямых плоскости;
· отношение подобия на множестве фигур плоскости;
· отношение равносильности на множестве уравнений;
· отношение "иметь одинаковые остатки при делении на фиксированное натуральное число m" на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают a 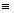 b (mod m);
b (mod m);
· отношение "принадлежать одному виду" на множестве животных;
· отношение "быть родственниками" на множестве людей;
· отношение "быть одного роста" на множестве людей;
· отношение "жить в одном доме" на множестве людей.
Отношения "жить на одной улице", "быть похожими" на множестве людей отношениями эквивалентности не являются, так как не обладают свойством транзитивности.
Из перечисленных выше свойств бинарных отношений следует, что пересечение отношений эквивалентности является отношением эквивалентности.
23. Понятие функции. Область определения и область значения функции.
Переменная величина 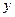 называется функцией переменной величины
называется функцией переменной величины 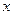 , если каждому значению
, если каждому значению 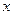 (которое она может принимать) соответствует единственное значение
(которое она может принимать) соответствует единственное значение 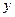 . Переменная величина
. Переменная величина 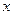 при этом называется независимой переменной или аргументом функции. Обозначения функции:
при этом называется независимой переменной или аргументом функции. Обозначения функции: 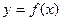 ,
, 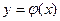 ,
, 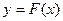 ,
, 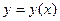 и т.п. Функцию и её аргумент можно обозначать и другими буквами.
и т.п. Функцию и её аргумент можно обозначать и другими буквами.
Множество всех значений аргумента, при которых функция принимает определённые действительные значения, называется областью определения этой функции. Множество всех значений функции называется областью её значений.
Значение, которое функция 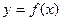 принимает при
принимает при 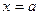 , обозначается
, обозначается 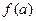 .
.
Корнемили нулём функции 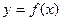 называется значение аргумента
называется значение аргумента 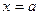 , при котором
, при котором 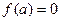 .
.
Если 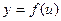 ,
, 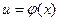 - функции своих аргументов, причём область определения функции
- функции своих аргументов, причём область определения функции 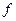 содержит область значений функции
содержит область значений функции 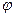 , то каждому
, то каждому 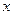 из области определения функции
из области определения функции 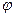 соответствует единственное
соответствует единственное 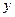 , такое что
, такое что 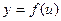 , где
, где 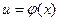 . Функция заданная подобным образом, обозначается
. Функция заданная подобным образом, обозначается 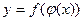 и называется функцией от функции или сложной функцией.
и называется функцией от функции или сложной функцией.
24. Отношение частичного порядка. Пример.
Определение 1. Бинарное отношение 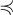 на множестве
на множестве 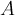 называется отношением частичного порядка1), если оно удовлетворяет свойствам
называется отношением частичного порядка1), если оно удовлетворяет свойствам
1. рефлексивности: 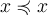 для всех
для всех 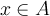 ;
;
2. антисимметричности: 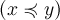
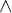
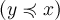
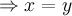 для всех
для всех 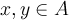 ;
;
3. транзитивности: 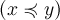
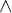
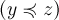
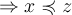 для всех
для всех 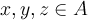 .
.
Пример 1. Пусть 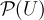 — множество всех подмножеств множества
— множество всех подмножеств множества 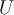 . Отношение включения
. Отношение включения 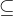 на
на 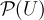 является отношением частичного порядка.
является отношением частичного порядка.
Пример 2. Упорядочение 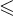 2) на множестве действительных чисел
2) на множестве действительных чисел 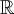 является отношением частичного порядка.
является отношением частичного порядка.
Пример 3. На множестве комплексных чисел 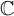 определим бинарное отношение
определим бинарное отношение 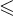 как множество упорядоченных пар комплексных чисел
как множество упорядоченных пар комплексных чисел 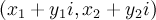 таких, что
таких, что 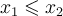 и
и 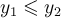 . Тогда
. Тогда 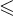 удовлетворяет свойствам
удовлетворяет свойствам
· рефлексивности;
· антисимметричности;
· транзитивности,
и по определению является отношением частичного порядка.
Пример 4. Отношение делимости на множестве целых чисел 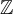 3) не является отношением частичного порядка, так как не обладает свойством антисимметричности: 2 делится на -2 и -2 делится на 2, но
3) не является отношением частичного порядка, так как не обладает свойством антисимметричности: 2 делится на -2 и -2 делится на 2, но 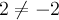 . Но то же самое отношение на множестве натуральных чисел
. Но то же самое отношение на множестве натуральных чисел  является отношением частичного порядка.
является отношением частичного порядка.
25. Инъекция, сюръекция и биекция.
Отображение называется инъекцией , если для любых элементов x1, x2 Î X , для которых f(x1) = f(x2) следует, что x1 = x2 . (рис. 7)
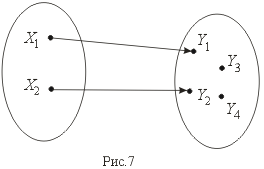
Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).
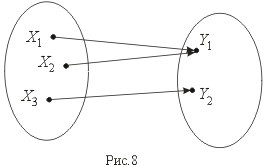
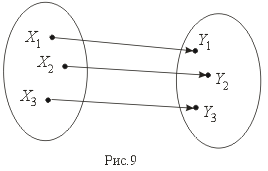
Биекция – это одновременно и сюръекция и инъекция (рис.9).
1. Испытания и исход.
Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание. Вообще говоря, эксперимент должен быть повторяемым. То есть, чтобы мы могли говорить о вероятности, у нас должна быть возможность провести эксперимент не один (а если совсем строго, то сколько угодно) раз.
Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: {выпало 6} и {выпало не 6}, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).
Испытанием называется эксперимент с очерченным набором возможных взаимоисключающих результатов. Эти результаты называются исходами.
2. Частота появления события.
Определение 1.Если проведена серия из 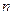 опытов, в каждом из которых могло появиться или не появиться некоторое событие
опытов, в каждом из которых могло появиться или не появиться некоторое событие 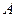 , то частотой события
, то частотой события 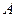 (статистической вероятностью события
(статистической вероятностью события 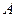 ) в данной серии опытов называется отношение числа
) в данной серии опытов называется отношение числа 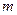 опытов, в которых появилось событие
опытов, в которых появилось событие 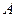 , к общему числу
, к общему числу 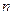 произведённых опытов:
произведённых опытов: 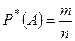 . (3.1)
. (3.1)
Замечание 1. При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Однако при увеличении числа опытов частота стабилизируется, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Это свойство устойчивости частот, многократно проверенное на опытах, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях. Проверить этот факт на практике можно только для событий, сводящихся к схеме случаев, так как только для этих событий существует точный способ вычисления математической вероятности. Многочисленные опыты этот факт действительно подтверждают.
Пример (опыт Бюффона и Пирсона). Бросание симметричной монеты.
| Число бросаний | Число выпадений герба | Частота выпадений герба |
| 0,5080 | ||
| 0,5016 | ||
| 0,5005 |
Вполне естественно допустить, что и для событий, не сводящихся к схеме случаев, тот же закон остаётся в силе и что постоянное значение, к которому при увеличении числа опытов приближается частота наступления события, представляет собой вероятность события. Тогда частоту события при достаточно большом числе опытов можно принять за приближенное значение вероятности
Математическую формулировку и доказательство этого факта представил Я. Бернулли. Он доказал, что при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.
Замечание 2. Характер приближения частоты к вероятности при увеличении числа опытов отличается от стремления к пределу в математическом смысле.
В математическом анализе 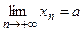 означает, что разность
означает, что разность 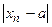 становится меньше любого положительного числа
становится меньше любого положительного числа 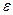 для всех значений
для всех значений 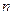 , начиная с некоторого достаточно большого числа.
, начиная с некоторого достаточно большого числа.
При экспериментальном определении вероятности через частоту события нет ничего физически невозможного в том, что при большом числе опытов частота события будет значительно уклоняться от его вероятности; но такое значительное уклонение является весьма маловероятным;тем менее вероятным, чем большее число опытов произведено. Пример: монета. Таким образом, при возрастании числа опытов частота приближается к вероятности, но не с полной достоверностью, а с большой вероятностью, которая при большом числе опытов может рассматриваться как практическая достоверность.
3. Статистическое определение вероятности.
Статистической вероятностью события А называется относительная частота появления этого события в произведённых испытаниях:
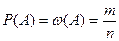
где 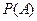 – вероятность появления события А;
– вероятность появления события А;
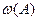 – относительная частота появления события А;
– относительная частота появления события А;
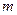 - число испытаний, в которых появилось событие А;
- число испытаний, в которых появилось событие А;
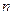 - общее число испытаний.
- общее число испытаний.
В отличие от классической вероятности статистическая вероятность является характеристикой опытной, экспериментальной.
Пример: Для контроля качества изделий из партии наугад выбрано 100 изделий, среди которых 3 изделия оказались бракованными. Определить вероятность брака.
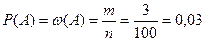 .
.
Статистический способ определения вероятности применим лишь к тем событиям, которые обладают следующими свойствами:
· Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
· События должны обладать статистической устойчивостью (или устойчи- востью относительных частот). Это означает, что в различных сериях испытаний относительная частота события изменяется незначительно.
· Число испытаний, в результате которых появляется событие А, должно быть достаточно велико.
Легко проверить, что свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности.
4. Случайная величина. Вероятность, математическое ожидание, дисперсия, среднеквадратичное отклонение.
Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)
Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)
Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.
Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: M(X) = x1p1 + x2p2 + ... + xnpn
Дата добавления: 2017-04-20; просмотров: 2219;
