Кинетическая энергия вращения

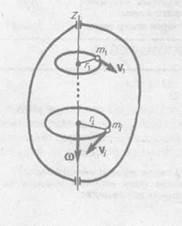
Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами m_1, т_2, ..., m_n, находящиеся на расстоянии г₁, r_2г,..., r_n,от оси.

При вращении твердого тела относительно неподвижной оси отдельные его элементар­ные объемы массами m_i опишут окружности различных радиусов г_i, и имеют различные

линейные скорости Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:

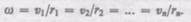(17.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

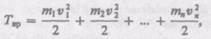или 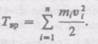Используя выражение (17.1), получаем

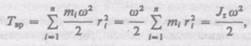
где 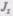— момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела

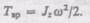(17.2)

Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно 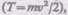следует, что момент инерции — мера инерт-

ности тела при вращательном движении. Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.

В случае плоского движения тела, например цилиндра, скатывающегося с наклон­ной плоскости без скольжения, энергия движения складывается из энергии поступатель­ного движения и энергии вращения:

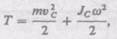
где т — масса катящегося тела; — скорость центра масс тела; 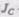— момент инер­ции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.

§ 18. Момент силы. Уравнение динамикивращательного движения твердого тела

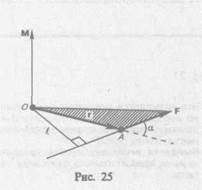
Момеятом силы F относительно неподвижвой точкиО называется физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точ­ки О в точку А приложения силы, на силу F (рис. 25):

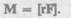
Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F. Модуль момента силы

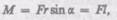(18.1)

где — угол между г и F; — кратчайшее расстояние между линией действия

силы и точкой О — плечо силы.

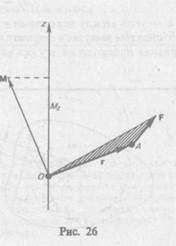
Моментом силы относительно неподвижной осиz называется скалярная величина 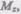равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента 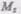не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела (рис. 27). Пусть сила F приложе­на в точке В, находящейся от оси z на расстоянии — угол между направлением силы и радиусом-вектором г. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол 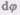точка приложения В проходит путь и работа равна произведе-

нию проекции силы на направление смещения на величину смещения:

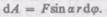(18.2)