Скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

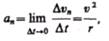
Называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

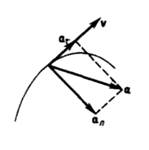
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):

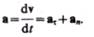
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) 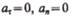— прямолинейное равномерное движение;

2) 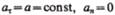прямолинейное равнопеременное движение. При таком виде движения

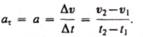
Если начальный момент времени 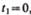, а начальная скорость то, обозначив

и 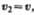получим 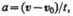откуда

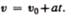
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

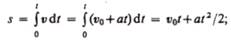
Рис. 5

3) 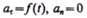— прямолинейное движение с переменным ускорением;

4) 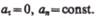При 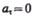скорость по модулю не изменяется, а изменяется по направлению. Из формулы 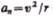следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) 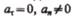— равномерное криволинейное движение;

6) 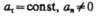— криволинейное равнопеременное движение;

7) 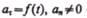— криволинейное движение с переменным ускорением.