Влияние увеличения размера выборки на точность оценок

Будем по-прежнему предполагать, что мы исследуем случайную переменную 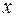с неизвестным математическим ожиданием 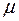и теоретической дисперсией 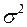и что для оценивания 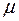используется 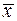. Каким образом точность оценки 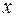зависит от числа наблюдений ?

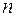Ответ неудивителен: при увеличении 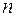оценка 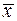, вообще говоря, становится более точной. В единичном эксперименте большая по размеру выборка необязательно даст более точную оценку, чем меньшая выборка, – всегда может присутствовать элемент везения, – но общая тенденция должна быть именно такой. Поскольку дисперсия 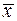выражается формулой 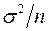(доказательство этого факта мы опускаем), она тем меньше, чем больше размер выборки, и, значит, тем сильнее «сжата» функция плотности вероятности для .

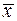Это показано на рис. A.9. Мы предполагаем, что 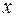нормально распределена со средним 25 и стандартным отклонением 50. Если размер выборки равен 25, то стандартное отклонение величины 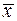, равное 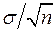, составит: 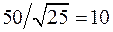. Если размер выборки равен 100, то это стандартное отклонение равно 5. На рис. А.9 показаны соответствующие функции плотности вероятности. Вторая ( 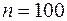) выше первой в окрестности 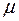, что говорит о более высокой вероятности получения с ее помощью аккуратной оценки. За пределами этой окрестности вторая функция всюду ниже первой.

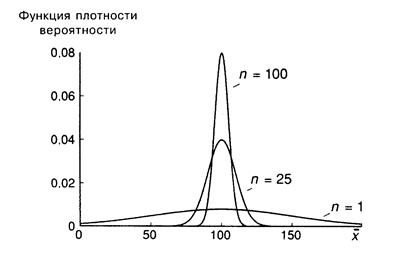
Рис. A.9.

Чем больше размер выборки, тем уже и выше будет график функции плотности вероятности для 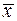. Если 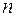становится действительно большим, то график функции плотности вероятности будет неотличим от вертикальной прямой, соответствующей 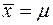. Для такой выборки случайная составляющая 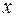становится действительно очень малой, и поэтому 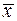обязательно будет очень близкой к 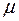. Это вытекает из того факта, что стандартное отклонение 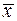, равное 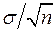, становится очень малым при больших .

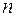В пределе, при стремлении 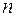к бесконечности, 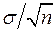стремится к нулю и 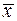стремится в точности к .

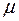Состоятельность

Вообще говоря, если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называется состоятельной. Иначе говоря, состоятельной называется такая оценка, которая дает точное значение для большой выборки независимо от входящих в нее конкретных наблюдений.

В большинстве конкретных случаев несмещенная оценка является и состоятельной. Для этого можно построить контрпримеры, но они, как правило, будут носить искусственный характер.

Иногда бывает, что оценка, смещенная на малых выборках, является состоятельной (иногда состоятельной может быть даже оценка, не имеющая на малых выборках конечного математического ожидания). На рис. A.10 показано, как при различных размерах выборки может выглядеть распределение вероятностей. Тот факт, что при увеличении размера выборки распределение становится симметричным вокруг истинного значения, указывает на асимптотическую несмещенность. То, что в конечном счете оно превращается в единственную точку истинного значения, говорит о состоятельности оценки.

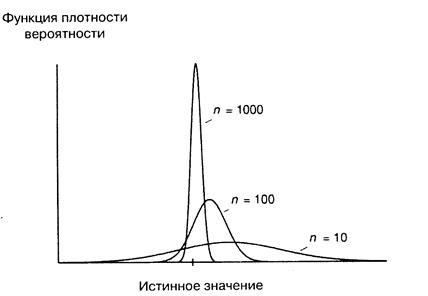
Рис. A.10.

Оценки, типа показанных на рис. A.10, весьма важны в регрессионном анализе. Иногда невозможно найти оценку, несмещенную на малых выборках. Если при этом вы можете найти хотя бы состоятельную оценку, это может быть лучше, чем не иметь никакой оценки, особенно если вы можете предположить направление смещения на малых выборках.

Нужно, однако, иметь в виду, что состоятельная оценка в принципе может на малых выборках работать хуже, чем несостоятельная (например, иметь большую среднеквадратичную ошибку), и поэтому требуется осторожность. Подобно тому, как вы можете предпочесть смещенную оценку несмещенной, если ее дисперсия меньше, вы можете предпочесть состоятельную, но смещенную оценку несмещенной или несостоятельную оценку им обеим (также в случае меньшей дисперсии).

Приложение B

Тестовые задания