Объясненная и необъясненная дисперсия результирующего показателя.

Цель регрессионного анализа состоит в том, чтобы объяснить поведение переменной Ув зависимости от изменения выбранных факторов X₁, Х₂,…, Х_n. В парном регрессионном анализе мы пытаемся объяснить поведение Упутем определения регрессионной зависимости У от фактораX. Для этой цели используется метод дисперсионного анализа.

Замечание: В математической статистике дисперсионный анализ рассматривается как самостоятельный метод статистического анализа. Мы же будем применять его как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идеи дисперсионного анализа общую сумму квадратов отклонений переменной у от среднего значения ӯ можно разложить на 2 части: объясненную и необъясненную:

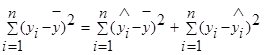
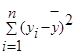- общая сумма квадратов отклонений (TSS ),

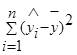- объясненная или регрессионная сумма квадратов (ESS ),

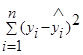- необъясненная или остаточная сумма квадратов (RSS ).

TSS=ESS+RSS.

Общая сумма квадратов отклонений значения результативного показателя от среднего значения вызвано множеством причин. Условно разделим всю совокупность на 2 группы: влияние изучаемого фактораX и влияние прочих факторов. Если фактор X не влияет наУ, то линия регрессии параллельна оси ОХ (ŷ=ӯ), тогда вся дисперсия результативного показателя обусловлена воздействием прочих факторов. TSS= RSS.

Если же прочие факторы не влияют на результат, тоУ связан с X функционально и остаточная сумма квадратов отклонений отсутствует. TSS=ESS.

Поскольку не все точки корреляционного поля лежат на линии регрессии, то всегда имеется их разброс, обусловленный влиянием как фактора X, так и воздействием прочих причин. Пригодность линии регрессии для прогноза зависит от того какая часть общего отклонения показывается У приходится на объясненную часть. Очевидно, что если ESS>RSS, то уравнение регрессии статистически значимо и фактор X оказывает существенное влияние на результативный показательУ.

Любая сумма квадратов отклонений связана с числом степеней свободы. Число степеней свободы fзависит от объема выборки n и от числа определенных по этой выборке параметров к (для линейной модели к=2, т.к. ŷ =а+bх) можно показать, что для общей TSS число степеней свободы f₁=n-1, для объясненной ESS - f₂=к-1, для необъясненной RSS – f₃=n-к.

TSS=ESS+RSS (4.1)

Разделив по членено каждое слагаемое равенства (4.1) на соответствующую ей степень свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы.

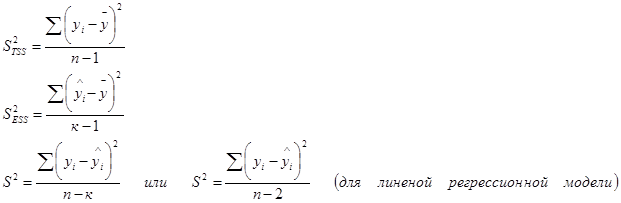
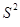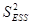и является несмещенными оценками дисперсии результирующего показателя обусловленных соответственно объясненной переменной х и под воздействием неучтенных случайных факторов.

Определение дисперсии на одну степень свободы приводит их к сравнимому виду и это используется в дальнейшем для проверки значимости влияния фактора х на результирующий показатель. (проверка фактора регрессии): для этого определяют:

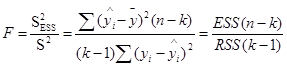(4.2)

Величина F называется F-критерием (отношение) Фишера.

Проверка статистических гипотез.

Статистической гипотезой H называется предположение относительно параметров или виды распределения случайной величины.

Нулевой (основной) называют выдвинутую гипотезу H0, альтернативной гипотезе H1, которая противоречит основной.

Проверку статистической гипотезы выполняют на основе результатов выборки. Поскольку выборка имеет ограниченный объем, то применяется возможность того, что будет отвергнута правильная нулевая гипотеза называемая уровнем значимости.

a = 5% (0,05) – это означает, что в 5 случаях из 100 верная гипотеза будет отвергнута.

Статистическим критерием (F или t) называется случайная величина, которая служит для проверки нулевой гипотезы. В качестве статистического критерия выбирается такая случайная величина точная или приближенная распределение, которой известно.

Наблюдаемым значением (Fнабл или tнабл) называется значение критерия вычисленного по данным выборки.

Множество значений критерия разбивают на 2 непересекающихся области: критическая и область принятия решений.

Критической областью называется совокупность значений критерии, при которой гипотеза H0 отвергается.

Область принятия решений – это совокупность значений критерия, при которых гипотеза H0 принимается.

Критическими точками называются точки отделяющие критическую область от области принятия решений, и обозначается (Fкр, tкр).

Критические точки определяются по таблицам известного распределения выборочного критерия при заданном уровне значимости a и числе степеней свободы f.

Сравнивая наблюдаемые значения критерия с критическими точками можно принять или отвергнуть нулевую гипотезу.

Пусть нулевая гипотеза состоит в том, что утверждается отсутствие связи между переменными.

Английский статистик Снедекор разработал статистические таблицы значений F – критерия при различных уровнях значимости a и различных степенях свободы f₂ и f₃.

если Fрас>Fтаб, то H0 отклоняется связь между Х и У существенна;

если Fрас<Fтаб, то H0 принимается уравнение регрессии статистически незначимо.

Для парной регрессии к=2 и уравнение регрессии статистически незначимо на уровне a, если

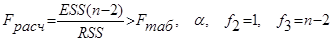
§ 1.5. Проверка гипотез, относящихся к коэффициентам регрессии и корреляции.

В линейной регрессии обычно оценивается значимость не только уравнения в целом (с F-теста), но и его параметров. Для этого по каждому параметру определяется его стандартная ошибка: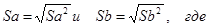

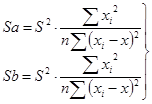(5.1) – называется исправленной выборочной дисперсией параметров а и b.

Пусть по выборочным данным получена оценка b. Чаще всего проверяется гипотеза H0: значимость коэффициента регрессии. Тогда t – статистика для коэффициента вычисляется по формуле: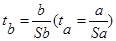

По таблице критических точек распределения Стьюдента по заданному уровню значимости a и данному числу степеней свободы f=n-2 находят критические значения tкр или tтаб. Вычисленный критерий 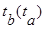сравнивается с критическим:

- если 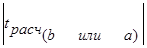< tкр, то H0 принимается, т.е. коэффициент данный незначим, и слагаемое отбрасывается

- если 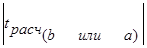> tкр, то H0 отклоняется, т.е. коэффициент данный значим.

Замечание: В эконометрических исследования проверку гипотез осуществляют при 5% и 1% уровне значимости.

Если H0 отклоняется при 1% уровне значимости, то она автоматически отклоняется и при 5% уровне; если H0 принимается при 5% уровне, то она принимается и при 1% уровне; если при 5% уровне гипотезы отклоняются, а при 1% принимается, то результаты проверки гипотез проводятся при обеих уровнях значимости.

В ряде прикладных задач требуется оценить значимость коэффициента корреляции r; для этого проверяется H0 о равенстве нулю теоретического коэффициента корреляции ρ=0. При этом исходят из того, что при отсутствии корреляционной связи статистика: 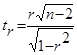(5.2) имеет t-распределение Стьюдента с n-2 степенями свободы. Коэффициента корреляции r значим на уровне a, если 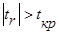, где tкр – это табличное значение t-критерия при уровне значимости a и числе степеней свободы f=n-2.

§ 1.2. Коэффициент корреляции.

Для оценки тесноты корреляционной зависимости используют выборочный коэффициент корреляции r или r(х,у).

где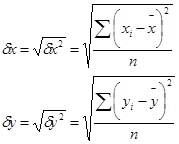

В этом уравнении (2.1) величина 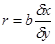показывает насколько величин dу изменится в среднем у, когда х увеличится dх. Величина r является показателем тесноты линейной связи между х и уи называется выборочным коэффициентом корреляции.

У

0 Х

Если r>0 (b>0), то корреляционная связь между переменными называются прямой, т.е. при увеличении значения переменной Х увеличивается значение условной средней переменной У.

Если r<0 (b<0), то связь обратная – при увеличении значения переменной Х значение условной средней уменьшается.

Выборочный коэффициент корреляции r при достаточно большом объеме выборке nтак же как и теоретический коэффициент корреляции r(х,у) обладает следующими свойствами:

1. значение коэффициента корреляции лежат в промежутке -1£r£1. Чем ближе ½r½к 1, тем теснее связь между Х и У.

2. При r=±1, то корреляционная связь между Х и У представляет собой линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.

У r=1 У r=-1

0 Х 0 Х

На практике такого идеального варианта не бывает.

3. При r = 0 – линейная корреляционная связь отсутствует при этом линия регрессии параллельна оси ОХ.

У

0 Х

Замечание:

Выборочный коэффициент корреляции r мы ввели исходя из близости точек корреляционного поля к прямой регрессии У на Х. Однако, в некоторых случаях (например, когда распределение случайных величин Х и У) не является нормальным или зависимость между Х и У не является линейным, то коэффициент r нельзя рассматривать как строгую меру связи между Х и У.

У

0 Х