В полубесконечном одномерном массиве

Метод функций Грина оказывается применимым не только к неограниченным пространственным областям, но и к полуограниченным и к ограниченным областям. Однако в этих случаях для удовлетворения появляющихся граничных условий функцию Грина рассматриваемой задачи приходится конструировать из функций Грина мгновенных точечных источников и диполей.

Задача 1. Пусть полубесконечный одномерный массив имеет в начальный момент времени постоянную температуру

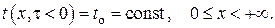
В момент времени 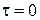поверхность массива 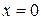мгновенно нагревается до температуры 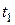, которая в дальнейшем поддерживается постоянной. Требуется найти распределение температур в массиве в произвольный момент времени .

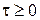Непосредственно использовать метод функций Грина в такой постановке задачи невозможно, так как этот метод применим только для неограниченной области .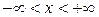

Тем не менее, задачу можно перепоставить, искусственно продолжив полуограниченный массив в отрицательную область 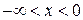, задав начальное условие в виде ступенчатой функции

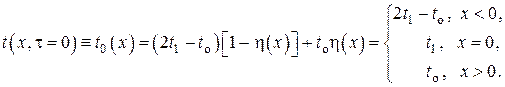
Здесь

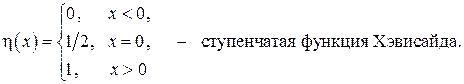
Представляется более удобным ввести относительную температуру

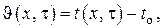
в соответствии с чем запишется в виде

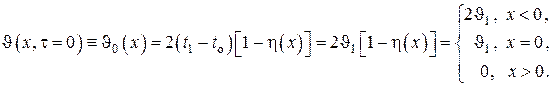
Используя , вычисляем

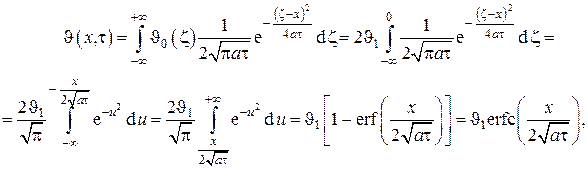
т.е. нестационарное температурное поле в полубесконечном одномерном массиве описывается известной в теории вероятностей функцией ошибок Гаусса или интегралом вероятности (см. рис. V.3).

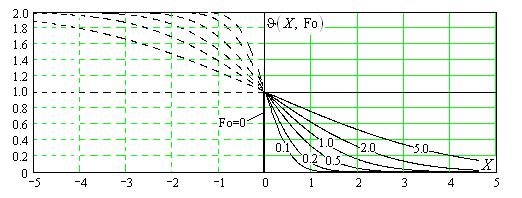
Рис. V.3. Эволюция температурного поля в одномерном полубесконечном массиве при ступенчатом изменении температуры поверхности

Задача 2. На плоскую поверхность 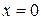полубесконечного массива с однородной в пространстве начальной температурой 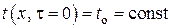подводится постоянный тепловой поток с плотностью 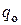. Найти нестационарное поле температур 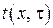в полупространстве .

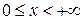Для решения этой задачи продолжим полупространство в отрицательную область до бесконечного пространства и введём на плоскости 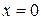постоянно действующий источник тепла мощностью 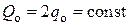. Тогда в соответствии с имеем

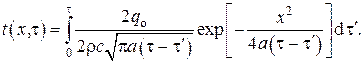
Заменой

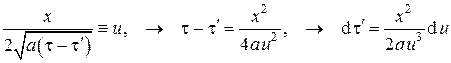
приводится к виду

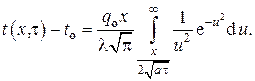
Интегрирование по частям даёт

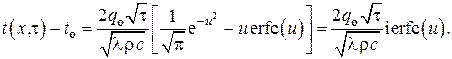
Здесь 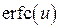– дополнительный интеграл вероятности, 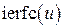– интегральный дополнительный интеграл вероятности.

На рис. V.4 и V.5 представлены графически в безразмерной форме зависимости температуры на различных расстояниях от обогреваемой поверхности от времени и для различных моментов времени от расстояния до обогреваемой поверхности соответственно.

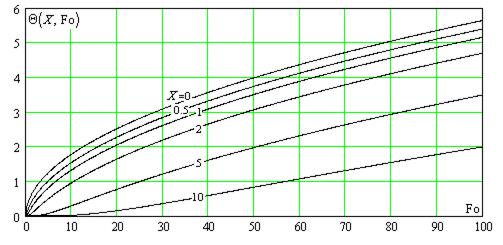
Рис. V.4. Эволюция во времени температурного поля в одномерном полубесконечном

массиве при действии постоянного теплового потока на поверхности

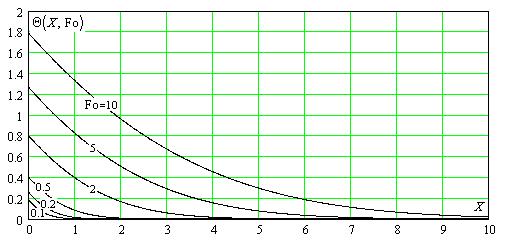
Рис. V.5. Эволюция в пространстве температурного поля в одномерном полубесконечном

массиве при действии постоянного теплового потока на поверхности