Глава IV. РЕШЕНИЕ ОДНОМЕРНЫХ НЕСТАЦИОНАРНЫХ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ В ОГРАНИЧЕННЫХ ОБЛАСТЯХ

Дифференциальное уравнение нестационарной теплопроводности с внутренними источниками теплоты в неподвижных изотропных средах с постоянными теплофизическими характеристиками имеет вид

Лапласиан 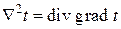для наиболее употребимых в инжереной практике системах координат имеет следующий вид:

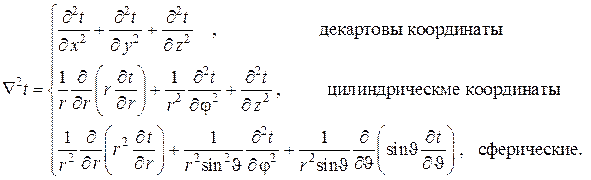
В математическом смысле дифференциальное уравнение теплопроводности представляет собой линейное неоднородное дифференциальное уравнение в частных производных второго порядка параболического типа. Если теплофизические характеристики среды 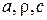не зависят от температуры, то уравнение является квазилинейным и допускает точные аналитические решения для многих пространственных областей с той или иной степенью симметрии.

В качестве краевых условий для задач теплопроводности примем:

– начальное условие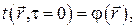

– граничное условие III рода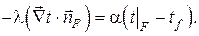

Общего стандартного метода решения уравнения теплопроводности для всех случаев краевых условий и пространственных областей не существует. Наиболее часто (исключая численные методы, получившие большое распространение в настоящее время в связи с развитием вычислительной техники) употребляются следующие методы:

– метод разделения переменных (метод Фурье);

– метод функций Грина (метод источников);

– метод интегральных преобразований;

– метод сведения к интегральному преобразованию; – метод итераций;
– метод малого параметра;

– вариационный метод;

– метод замены независимых переменных на зависимые и обратно;

– метод Бубнова-Галёркина; и т. д.

Мы будем в дальнейшем решать одномерные задачи теплопроводности с координатой r в качестве независимой пространственной переменной, т. е.

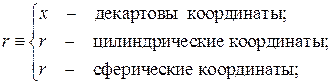
Будем также в дальнейшем считать

Таким образом, в прямоугольной, цилиндрической и сферической системах координат имеем соответственно:

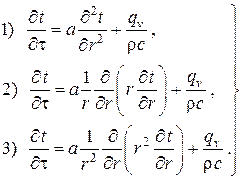
Легко видеть, что все эти три случая могут быть записаны в общем виде

где

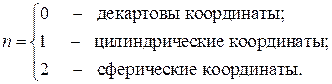
Краевые условия для одномерных задач записываются в виде:

– начальные условия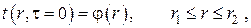

– граничные условия

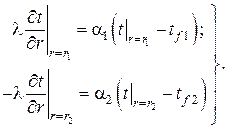
Для удобства приведём задачу к безразмерному виду, введя безразмерные переменные, функции и комплексы:

– безразмерная координата

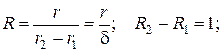
– безразмерное время (число Фурье)

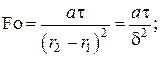
– безразмерная температура

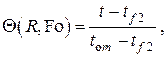
где 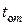– некоторая начальная температура тела, в качестве которой можно выбрать среднюю по объёму тела температуру, которая в одномерном случае определится интегралом

– критерий Био

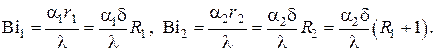
В этом случае поставленная задача принимает вид

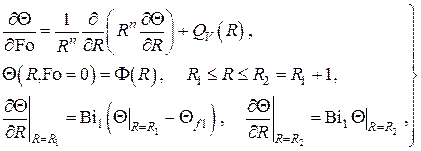
где

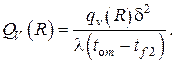
В силу линейности дифференциального уравнения и краевых условий представим искомое решение для температурного поля в виде суммы

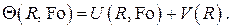
В этом случае задача может быть разделена на две независимые подзадачи для функций :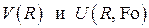

А) Стационарная задача для функции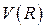

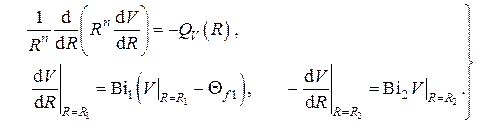
Б) Нестационарная задача для функции

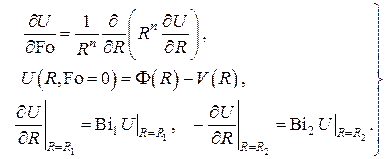
Задача А)

Общее решение стационарной задачи А) имеет вид

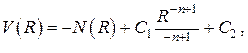
где обозначено

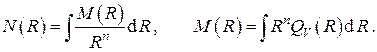
Очевидно, что в отсутствие внутренних тепловыделений 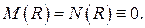Если мощность внутренних источников тепла постоянна по объёму, то

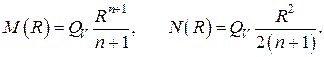
Постоянные находятся из граничных условий в . Простые, однако громоздкие алгебраические преобразования приводят к следующему результату

Опуская громоздкие алгебраические преобразования с использованием при необходимости вычисления пределов с помощью правила Лопиталя приведём следующие из ­– частные случаи для декартовых, цилиндрических и сферических координат.

– Декартовы координаты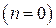

Если положить 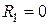при условии, что плотность внутренних источников 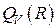тепла растёт с уменьшением 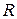не быстрее, чем 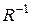, то решение принимает вид

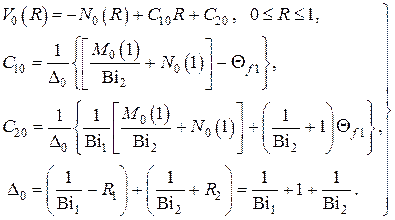
Для случая имеем

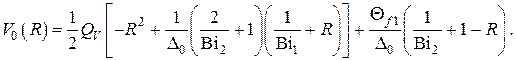
В отсутствие внутренних тепловыделений

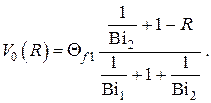
Переходя к размерным величинам в соответствии с определениями – получаем известный результат стационарного линейного распределения температуры по толщине однородной плоской стенки без внутренних источников теплоты при граничных условиях III рода и плотности теплового потока

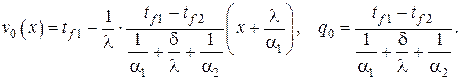
– Цилиндрические координаты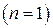

При выборе цилиндрической системы координат взятие предела 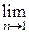в решении с использованием правила Лопиталя с учётом даёт следующий результат

В случае с учётом имеем

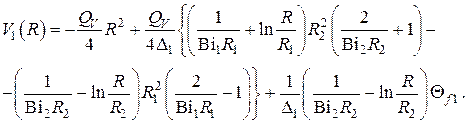
Если внутренняя поверхность 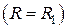теплоизолирована 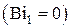, то

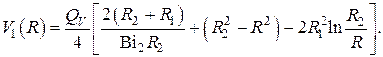
И наконец для сплошного цилиндра 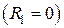с однородным тепловыделением

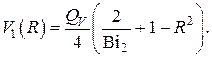
– Сферические координаты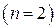

Полагая в – n=2 получаем

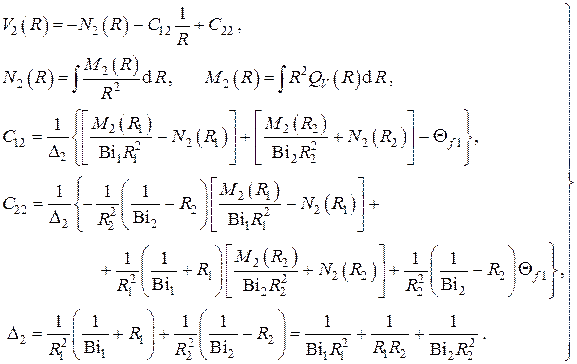
В случае идеальной теплоизоляции внутренней поверхности сферической стенки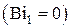

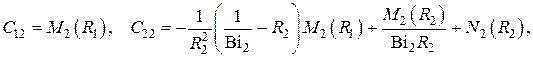
Для сплошного шара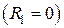

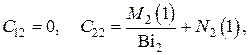
т.е. при однородном тепловыделении в сплошном шаре

Задача Б)

Будем решать однородную нестационарную задачу в ограниченной области методом разделения переменных (методом Фурье), для чего представим искомую функцию 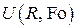в виде произведения двух функций, каждая из которых зависит только от одной переменной, т.е.

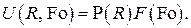
Подставив это представление в исходное дифференциальное уравнение , получим

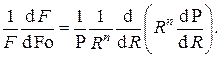
Получившееся равенство двух выражений слева и справа, зависящих каждое от различных независимых переменных, возможно только в том случае, если каждое из них равняется одной и той же постоянной. Имеем таким образом

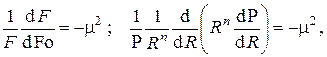
где m – некоторое действительное число, подлежащее вычислению в дальнейшем. Знак «–» перед 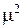выбран из физических соображений, требующих конечности температуры при стремлении времени к бесконечности.

Временнàя часть задачи представляется экспонентой

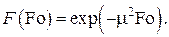
Для пространственной составляющей 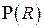имеем однородное линейное дифференциальное уравнение с однородными граничными условиями, следующими из

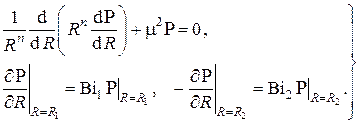
Запишем дифференциальное уравнение для 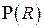в компактной форме

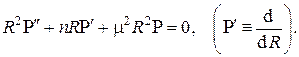
Одно из частных решений этого уравнения будем искать в виде сходящегося степенного ряда

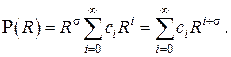
Подставив это представление в дифференциальное уравнение , получаем степенной функциональный ряд

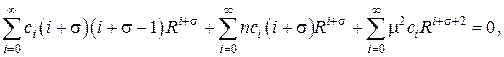
сумма которого должна быть тождественно равна нулю. Такое возможно, только если коэффициенты при всех степенях R равны нулю. Группируя слагаемые с одинаковыми степенями R , получаем следующие соотношения

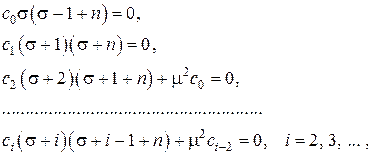
позволяющие последовательно находить коэффициенты разложения 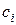при известных 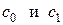с помощью рекуррентного соотношения

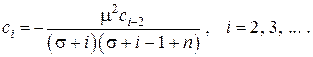
Первые два выражения в оставляют некоторый произвол для выбора величин 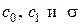, а именно

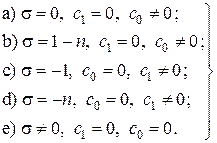
Случай e) даёт, очевидно, тривиальное решение 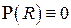и не представляет интереса. В качестве нетривиального случая выберем вариант а), положив без уменьшения общности 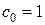. Тогда все нечётные коэффициенты в исчезают, а все чётные коэффициенты связываются рекуррентным соотношением

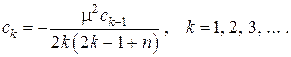
Решение записывается тогда в виде

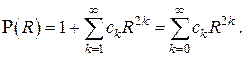
Вычисляя последовательно коэффициенты 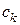на основании рекуррентного соотношения , получаем

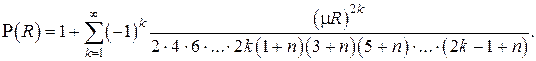
Второе линейно независимое решение уравнения может быть найдено с использованием функционального определителя Вронского

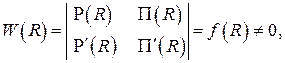
позволяющего записать дифференциальное уравнение первого порядка для искомого второго решения

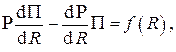
решение которого есть

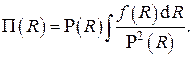
Рассмотрим частные случаи решения для различных систем координат.

– Декартовы координаты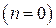

Полагая в n=0 и перегруппируя сомножители в знаменателе, получаем

что представляет собой не что иное как разложение в ряд Тэйлора функции косинуса, т.е.

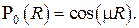
Второе линейно независимое решение есть

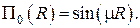
– Цилиндрические координаты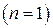

В случае цилиндрических координат решение принимает вид

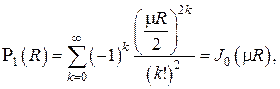
где 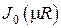есть функция Бесселя первого рода нулевого порядка от действительного аргумента. Второе линейно независимое решение представляет собой функцию Бесселя второго рода нулевого порядка

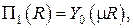
явный вид которой ввиду её громоздкости выписывать не будем.

– Сферические координаты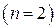

При 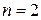ряд преобразуется к виду

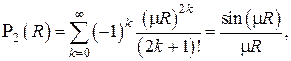
а второе линейно независимое решение

Таким образом, одно из частных решений задачи Б) будет

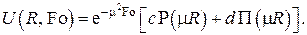
Используя граничные условия для функции 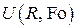в , получаем однородную систему двух линейных алгебраических уравнений для неизвестных коэффициентов c и d

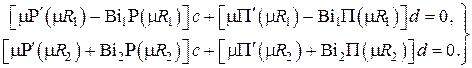
Как известно, однородная система алгебраических уравнений позволяет найти только отношение неизвестных 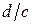, причём решение будет нетривиальным только в случае, если определитель этой системы равен нулю. Имеем тогда

Равенство первых двух дробей и этом представлении носит название секулярного (векового) уравнения, которое позволяет найти значение константы 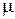, впервые появившейся в . Секулярное уравнение в большинстве задач математической физики имеет бесконечное число действительных корней, которые находятся, как правило, численно. Расположив корни 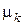в порядке возрастания, запишем общее решение для 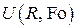в виде бесконечной суммы

Бесконечное количество отношений 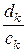находятся из для различных значений 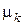. Коэффициенты разложения 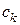находятся из начального условия в

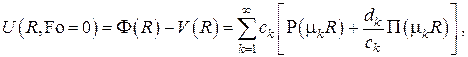
которое представляет собой разложение функции 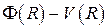в обобщённый ряд Фурье по системе функций

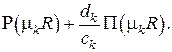
Коэффициенты разложения 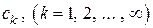могут быть найдены, если система функций ортогональна, т. е. если

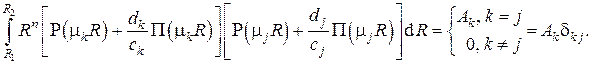
Покажем ортогональность этой системы функций. Обозначим для краткости

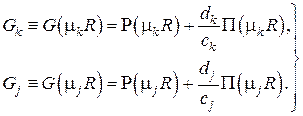
Поскольку функции 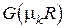, являясь линейными комбинациями частных решений 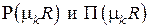, сами являются решениями и удовлетворяют граничным условиям, то можно записать

Умножив первое уравнение на 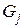, а второе – на 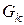и вычтя их почленно, получим

или, используя известные теоремы дифференциального исчисления,

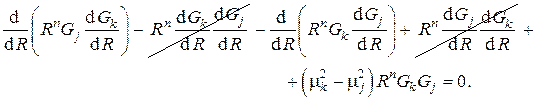
Интегрируя это выражение в пределах 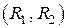, получаем

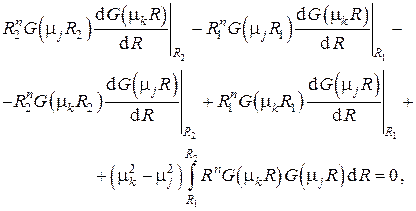
а используя граничные условия в , имеем

откуда следует

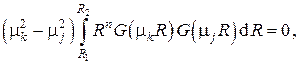
т. е. при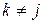

а при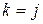

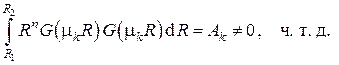
Заметим, что в этом выражении 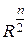носит название весовой функции.

Ввиду ортогональности системы функций 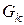коэффициенты 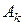находятся интегрированием

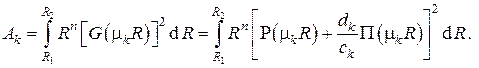
Таким образом, из с учётом ортогональности системы функций находим коэффициенты разложения в решении нестационарной задачи

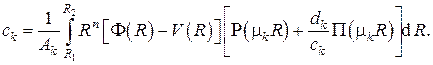
Этой операцией завершается решение одномерных линейных нестационарных задач теплопроводности в ограниченных областях с внутренними стационарными источниками теплоты. Выпишем это решение в явном виде с учётом , , , , , , и :

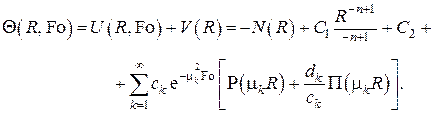
В качестве примера изложенного выше метода рассмотрим классическую задачу охлаждения плоской пластины 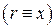с одинаковыми условиями теплообмена с обеих сторон 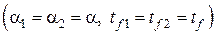при граничных условиях III рода без внутренних источников теплоты 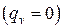с однородным распределением температуры в начальный момент времени .

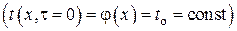В этом случае n=0, а в соответствии с определениями , решение стационарной задачи оказывается нулевым, т. е.

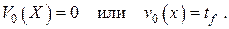
Подставим линейно независимые решения и в секулярное уравнение

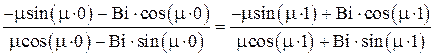
или

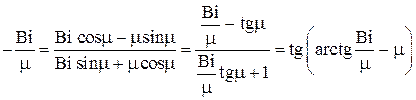
Отсюда получаем трансцендентное алгебраическое уравнение для нахождения μ

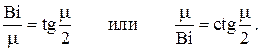
Это уравнение имеет бесконечное множество действительных корней и может быть решено только численно. Графически корни этого уравнения представляются абсциссами точек пересечения прямой 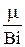с ветвями котангенсоиды .

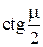Отношения находим из . Вычисления дают

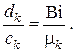
Тогда фундаментальная система функций будет

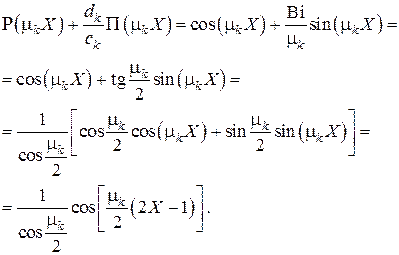
Коэффициенты разложения 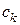в находим из с учётом того, что и 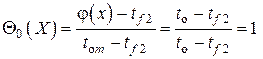. Имеем

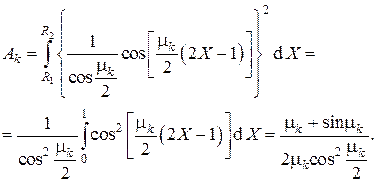
Вычисления по дают

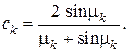
Таким образом, решение поставленной простейшей задачи остывания (нагрева) однородной бесконечной плоской пластины с одинаковыми условиями теплообмена с обеих сторон при граничных условиях III рода без внутренних источников теплоты с однородным распределением температуры в начальный момент времени в безразмерной форме представляется в виде

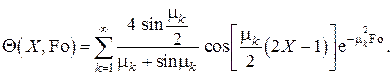
Замечание

Обычно в задачах с пространственной симметрией, подобной рассматриваемой, в качестве линейного масштаба выбирается половина толщины пластины. Тогда обозначив полную толщину пластины как с учётом переопределений критериев Био и Фурье, а также смещая начало координаты X в среднюю плоскость пластины, решение запишем в виде, который приводится в учебной и справочной литературе,

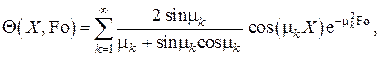
где – половина толщины пластины,

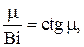
Приведём первые несколько корней этого трансцендентного уравнения, полученные численным методом (см. табл. 1).

Из таблицы и из графика легко видеть, что при малых значениях критерия Bi (при большой теплопроводности λ материала пластины и/или малом коэффициенте теплоотдачи α) корни уравнения , начиная с μ₂ и выше, с большой степенью точности оказываются кратными числу π, т.е. Значение μ₁ при малых Bi может быть оценено с помощью разложения в ряд Тэйлора выражения

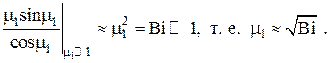
Таблица 1

Корни уравнения для различных значений критерия Bi

Bi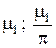
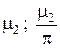
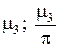
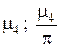
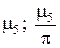
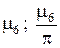
0.1	0.311; 0.099	3.173; 1.010	6.299; 2.005	9.435; 3.003	12.57; 4.003	15.71; 5.002
0.5	0.653; 0.208	3.292; 1.048	6.362; 2.025	9.477; 3.017	12.61; 4.013	15.74; 5.010
	0.860; 0.274	3.426; 1.090	6.437; 2.049	9.529; 3.033	12.65; 4.025	15.77; 5.020
	1.077; 0.343	3.644; 1.160	6.578; 2.094	9.630; 3.065	12.72; 4.050	15.83; 5.040
	1.314; 0.418	4.034; 1.284	6.910; 2.199	9.893; 3.149	12.94; 4.117	16.01; 5.096
	1.429; 0.455	4.306; 1.371	7.228; 2.301	10.200; 3.247	13.214; 4.206	16.259; 5.176

Графическое представление уравнения для Bi=1 приведено на рис. IV.1.

Имея в виду, что при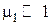

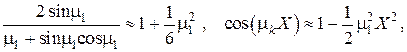
в линейном приближении по 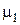решение принимает простейший вид

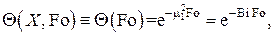
т.е. при малых Bi температура в материале пластины не зависит от координаты и изменяется экспоненциально со временем. В размерных величинах это решение записывается в виде

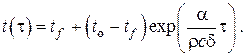
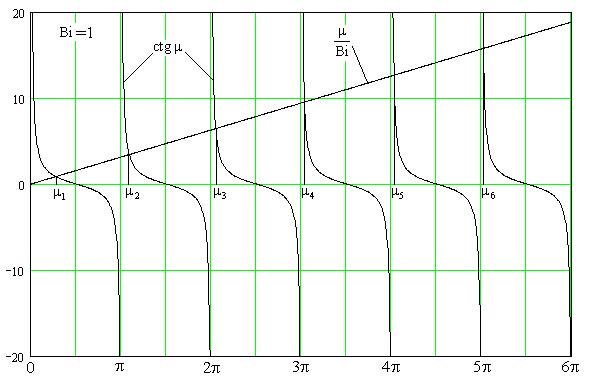
Рис.IV.1. К графическому нахождению корней характеристического уравнения

Отметим, что такой же результат справедлив в тех же приближениях для тел произвольной формы с заменой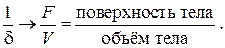

Рассмотрим теперь случай больших значений критерия Bi, что имеет место для тел с низкой теплопроводностью. Тогда решениями будут значения

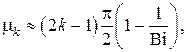
а поле температур в пренебрежении слагаемыми с принимает вид

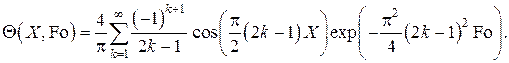
На рисунке IV.2 представлены графически рассчитанные в математическом пакете MathCAD 2001 температурные поля в плоской стенке для различных моментов времени

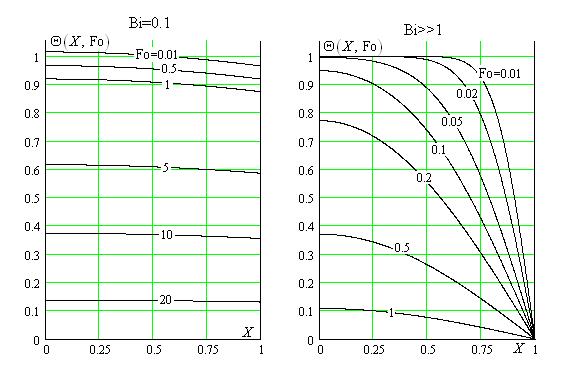
Рис.IV.2. Нестационарные температурные поля в плоской стенке из высоко- теплопроводного материала (Bi=0.1) и из теплоизоляционного материала (Bi>>1)