Бесконечно малые и бесконечно большие функции
Функция 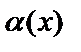 называется бесконечно малой при
называется бесконечно малой при 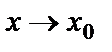 , если
, если 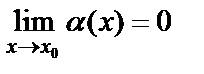 . Бесконечно малые функции обладают следующими свойствами:
. Бесконечно малые функции обладают следующими свойствами:
1) алгебраическая сумма конечного числа бесконечно малых функций есть функция бесконечно малая;
2) произведение конечного числа бесконечно малых функций есть функция бесконечно малая;
3) произведение ограниченной величины на бесконечно малую функцию есть функция бесконечно малая.
Рассмотрим бесконечно малые функции 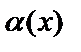 и
и 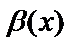 , т.е.
, т.е. 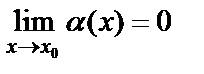 и
и 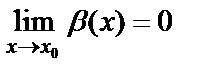 . Так как эти бесконечно малые функции могут стремиться к нулю при
. Так как эти бесконечно малые функции могут стремиться к нулю при 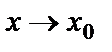 с разными скоростями, то для их сравнения находится предел отношения этих функций
с разными скоростями, то для их сравнения находится предел отношения этих функций 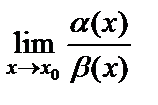 . При этом возможны следующие случаи:
. При этом возможны следующие случаи:
1) если 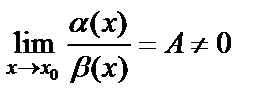 (А – конечное число), то
(А – конечное число), то 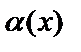 и
и 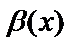 называются бесконечно малыми функциями одного порядка;
называются бесконечно малыми функциями одного порядка;
2) если 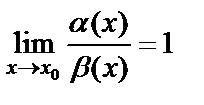 , то
, то 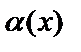 и
и 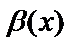 называются эквивалентными бесконечно малыми функциями при
называются эквивалентными бесконечно малыми функциями при 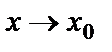 ; в этом случае предел отношения двух бесконечно малых функций не изменится, если каждую из них или какую-либо одну заменить им эквивалентными;
; в этом случае предел отношения двух бесконечно малых функций не изменится, если каждую из них или какую-либо одну заменить им эквивалентными;
3) если предел 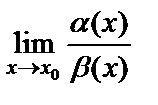 не существует, то бесконечно малые функции
не существует, то бесконечно малые функции 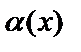 и
и 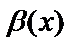 называются несравнимыми.
называются несравнимыми.
Функция 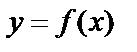 называется бесконечно большой функцией в точке
называется бесконечно большой функцией в точке 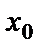 , если для всех значений х, достаточно близких к
, если для всех значений х, достаточно близких к 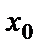 , соответствующие значения функции по абсолютной величине превосходят любое наперёд заданное сколь угодно большое положительное число, т.е.
, соответствующие значения функции по абсолютной величине превосходят любое наперёд заданное сколь угодно большое положительное число, т.е. 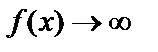 при
при 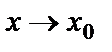 или
или 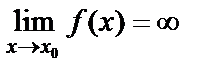 .
.
Пусть 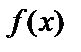 есть бесконечно большая функция при
есть бесконечно большая функция при 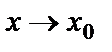 , тогда функция
, тогда функция 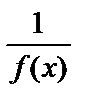 является бесконечно малой функцией при
является бесконечно малой функцией при 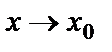 . Если
. Если 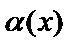 есть бесконечно малая функция при
есть бесконечно малая функция при 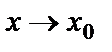 , то
, то 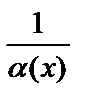 является бесконечно большой функцией при
является бесконечно большой функцией при 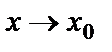 .
.
Например, функция 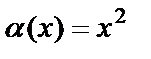 при
при 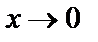 является бесконечно малой функцией. Тогда функция
является бесконечно малой функцией. Тогда функция 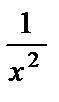 при
при 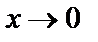 является бесконечно большой. Функция
является бесконечно большой. Функция 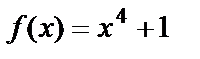 при
при 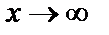 является бесконечно большой. Тогда
является бесконечно большой. Тогда 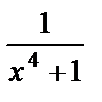 при
при 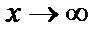 будет бесконечно малой функцией.
будет бесконечно малой функцией.
Предел 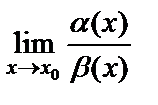 отношения бесконечно малых функций может быть конечным, бесконечным или же вообще не существует. В этом случае выражение
отношения бесконечно малых функций может быть конечным, бесконечным или же вообще не существует. В этом случае выражение 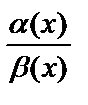 при
при 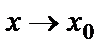 называется неопределённостью вида
называется неопределённостью вида 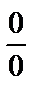 .
.
Пусть 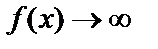 и
и 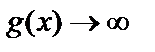 при
при 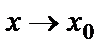 , т.е.
, т.е. 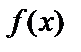 и
и 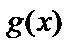 являются бесконечно большими функциями в точке
являются бесконечно большими функциями в точке 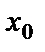 . Предел отношения этих функций может быть конечным, бесконечным или вообще не существует. Выражение
. Предел отношения этих функций может быть конечным, бесконечным или вообще не существует. Выражение 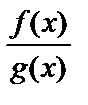 при
при 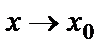 называется неопределённостью вида
называется неопределённостью вида 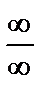 , а выражение
, а выражение 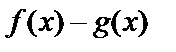 называется неопределённостью вида
называется неопределённостью вида 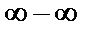 .
.
Если 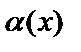 - бесконечно малая функция, а
- бесконечно малая функция, а 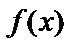 - бесконечно большая при
- бесконечно большая при 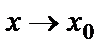 , то выражение
, то выражение 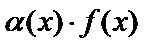 называется неопределённостью вида
называется неопределённостью вида 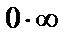 . Аналогично вводятся неопределённости вида
. Аналогично вводятся неопределённости вида 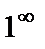 ,
, 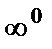 ,
, 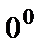 . Чтобы раскрыть неопределённость, нужно найти соответствующий предел.
. Чтобы раскрыть неопределённость, нужно найти соответствующий предел.
Пример 6. Найти предел функции 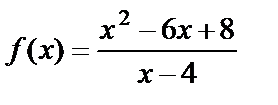 при
при 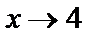 .
.
Решение. Подставим предельное значение х=4 в функцию:
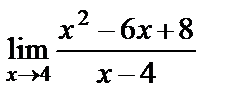 =
= 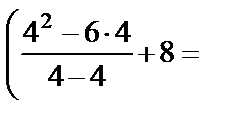
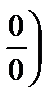 . Получена неопределённость вида
. Получена неопределённость вида 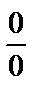 . Для её раскрытия найдём корни квадратного трёхчлена, записанного в числителе, и разложим его на множители:
. Для её раскрытия найдём корни квадратного трёхчлена, записанного в числителе, и разложим его на множители: 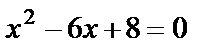 ,
, 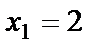 ,
, 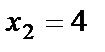 ,
, 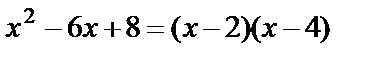 . Подставим разложение в числитель:
. Подставим разложение в числитель: 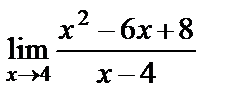 =
= 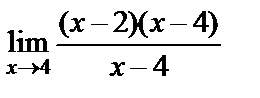 =
= 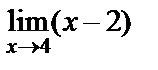
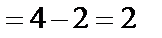 .
.
Пример 7. Найти предел функции 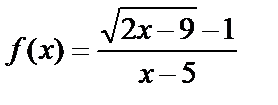 при х=5.
при х=5.
Решение. Подставим вначале значение х=5 в функцию:
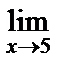
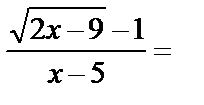
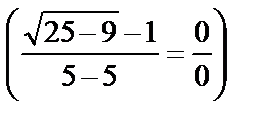 . Для раскрытия полученной неопределённости числитель и знаменатель функции умножим на выражение
. Для раскрытия полученной неопределённости числитель и знаменатель функции умножим на выражение 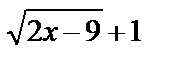 , сопряжённое числителю, и выполним необходимые преобразования:
, сопряжённое числителю, и выполним необходимые преобразования:
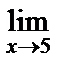
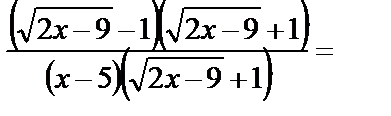
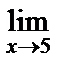
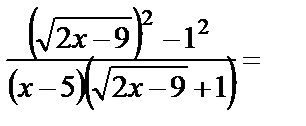
= 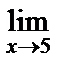
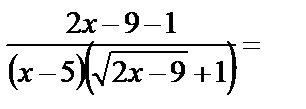
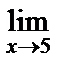
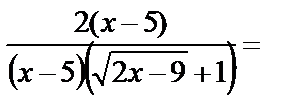
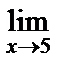
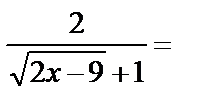
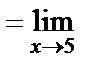
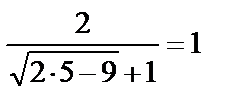 .
.
Пример 8. Найти предел функции 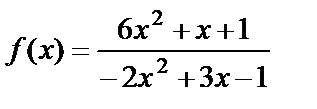 при
при 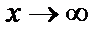 .
.
Решение. Подставим в функцию вместо переменной х её предельное значение: 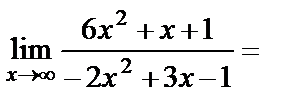
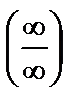 . Получена неопределённость вида
. Получена неопределённость вида 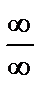 . Для её раскрытия каждый член числителя и знаменателя разделим на
. Для её раскрытия каждый член числителя и знаменателя разделим на 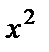 и вычислим предел:
и вычислим предел:
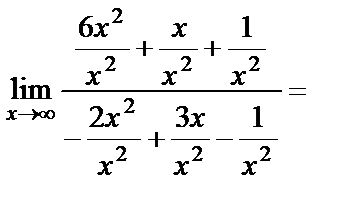
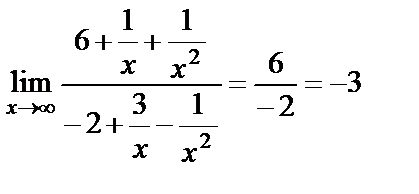 , так как функции
, так как функции 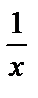 ,
, 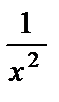 ,
, 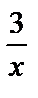 являются бесконечно малыми при
являются бесконечно малыми при 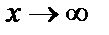 .
.
Предел 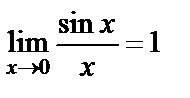 называется первым замечательным пределом. Пусть
называется первым замечательным пределом. Пусть 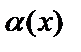 - есть бесконечно малая функция при
- есть бесконечно малая функция при 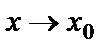 . Тогда
. Тогда 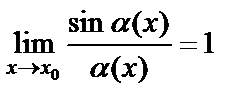 . Предел
. Предел 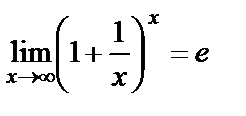 или
или 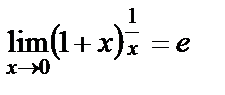 называется вторым замечательным пределом.
называется вторым замечательным пределом.
Пример 9. Найти предел функции 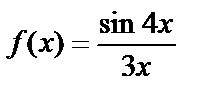 при
при 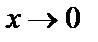 .
.
Решение. 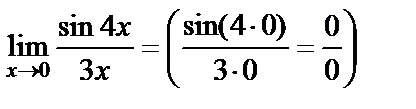 . Для раскрытия неопределённости
. Для раскрытия неопределённости 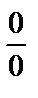 воспользуемся первым замечательным пределом:
воспользуемся первым замечательным пределом:
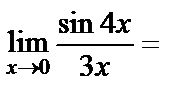
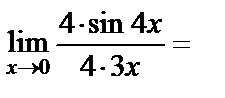
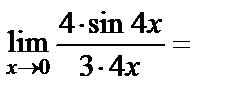
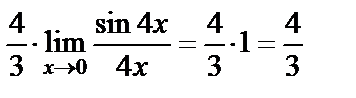 .
.
Пример 10. Найти предел 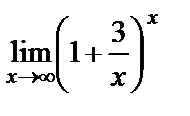 .
.
Решение. Воспользуемся формулой второго замечательного предела 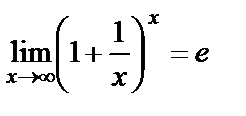 :
:
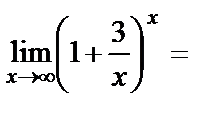
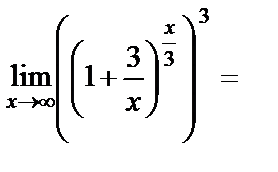
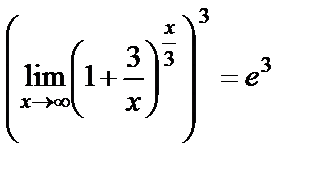 .
.
Дата добавления: 2015-12-10; просмотров: 2136;
