Условная оптимизация нелинейных моделей

Существует класс задач в которых целевая функция нелинейно зависит от компонент вектора проектных параметров, либо нелинейны ограничения целевой функции.

Эти задачи изучают в специальном разделе мате­матики — нелинейном программиро­вании (НП).

При решении задач условной оптимизации НП находят применение способы статистического разыгрывания. Эти ме­тоды основаны на случайном выборе точек в пространстве векторов проектных параметров Rⁿ, и, как правило, не имеют строгого математического обоснования. Однако они логически просты, и позволяют достаточно быстро приблизиться к оптимуму.

В качестве одного из таких методов оптимизации часто используется комплекс-метод. Этот способ оптимизации может с успехом применяться как для задач безусловной, так и условной оптимизации. В послед­нем случае на область проектных параметров накладывается дополнительное требование выпуклости.

Метод комплексов напоминает симплексный поиск, однако в отличие от регулярных симплексов вершины комплексов строятся статистическим разыгрыванием.

Первоначальный комплекс имеет число вер­шин N>п+1, при n<5 рекомендуется брать N=2п. Его вершины строят статистическим разыгрыванием, сущность которого состоит в следующем. Пусть a_i и b_i — соответственно границы изменения i-го компонента x_i вектора проектных па­раметров (a_i≤х_i≤b_i). Тогда i-й компонент j-й вершины определяют по формуле

в которой случайное число r_ijÎ[0,1] может быть получено с помощью специальных программ — датчиков псевдослучайных чисел.

При формировании компонент вектора каждой вершины проверяют соответствие координат вершин заданным огра­ничениям. Если полученный набор проектных параметров в какой-нибудь вершине не удовлетворяет ограничениям — вер­шина вышла за пределы допускаемой области решений, то он отбрасывается и заменяется новым.

После завершения расчетов компонент векторов всех вер­шин комплекса в них рассчитывают значения целевой функ­ции. Сопоставляя между собой полученные N значений, вы­бирают вершину с наихудшим значением целевой функции (при разыскании минимума вершину комплекса с наибольшим значением целевой функции, при разыскании максимума — с наименьшим).

Затем вычисляют координаты центра тяжести полученных вершин комплекса без худшей вершины по формуле

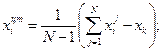
(32.1)

где k – номер худшей вершины комплекса. Требование вы­пуклости области задания векторов проектных параметров, накладываемое на ограничения, обеспечивает попадание цен­тра тяжести в заданную область.

Следующий шаг алгоритма комплекс-метода — отражение худшей вершины относительно центра тяжести остальных (32.1). Отражение осуществляют по формуле

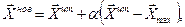
где α – масштабный коэффициент. Первоначально полагают α=1; если вновь полученная вершина не попадает в область задания, то эту точку приближают к 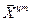, положив .

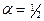После этого рассчитывают среднее значение целевой функции и координаты вектора центра тяжести всех N вер­шин комплекса:

;

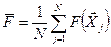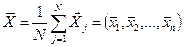
Затем проверяют выполнение условий окончания работы ал­горитма комплекс-метода:

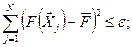(32.2)

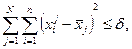(32.3)

где ε и δ – заранее заданные точности вычисления це­левой функции и координат соответственно. Если условия (32.2) и (32.3) выполнены, то лучшая из вершин последнего ком­плекса принимается за оптимальное решение. Если ус­ловия на данном шаге не выполняются, то пока они не будут выполнены продолжают по­следовательно отражать худшие вершины,.

Достаточно просты и удобны в практическом использова­нии методы условной оптимизации задач НП, основанные на преобразовании задачи условной оптимизации в задачу безусловной оптимизации за счет введения вспомогатель­ных — штрафных функций.

Идея метода штрафных функций состоит в сле­дующем. Пусть требуется минимизировать функцию f(X) при ограничениях (28.2)-(28.4). В наиболее общем виде штрафная функция задается выражением

(32.4)

где 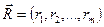– вектор штрафных параметров; Ω – штраф, являющийся функцией штрафных параметров, а также функцией ограничений (28.3), (28.4). Штраф Ω должен быть сконструирован таким образом, чтобы при приближении точки к границе допустимой области, задаваемой ограниче­ниями, штрафная функция при разыска­нии минимума) резко возрастала. Используя методы безусловной оптимиза­ции, находят такие значения проектных и штрафных пара­метров, при которых Ф (32.4) достигает минимума. При этом, как правило, приходится строить последовательность векторов проектных и штрафных параметров, сходящуюся к точке оптимума.

В настоящее время наиболее разработан аппарат ЛП, поэтому представляется рациональным в ряде случаев использовать его для оптимизации нелинейных функций.

Наиболее просто это осуществить линеаризацией целевой функции (28.1) и функций – ограничений (28.2), (28.3), т. е.заменой нелинейных функций линейными приближениями. С этой целью рационально использовать разложе­ние целевой функции и функций-ограничений в ряд Тейлора, ограничиваясь линейными членами. В результате линейной аппроксимацией целевой функции принимается:

(32.5)

в которой называется точкой линеариза­ции. Аналогично строятся линейные аппроксимации ограни­чений:

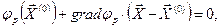
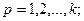(32.6)

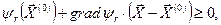
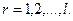(32.7)

Решая оптимизационную задачу ЛП (32.5)-(32.7), напри­мер, симплекс-методом, получают точку пространства проектных параметров, которая является первым при­ближением к оптимуму. Далее, заменив 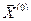на X(1), получают аналогично новое приближение и т. д.

Существует ряд алгоритмов, совер­шенствующих описанную выше итерационную процедуру. Они позволяют построить последовательность векто­ров проектных параметров, приближающихся к точке опти­мума для различных конкретных задач НП.

Лекция №33