Принцип независимости действия сил
Допущение о малости деформаций делает возможным применение принципа независимости действия сил. Этот принцип в сопротивлении материалов формулируется следующим образом: результат одновременного действия нескольких групп сил совпадает с суммой результатов, вызванных каждой группой сил в отдельности.
Для доказательства данного принципа рассмотрим двухопорную балку, изображенную на рис. 1.14. Приложим в некоторой произвольной точке силу Р1, которая вызовет в точке А перемещение 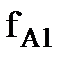 , которое равно
, которое равно 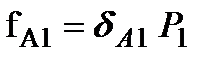 , где
, где 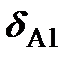 - коэффициент пропорциональности. Теперь устраним действие силы Р1 и в некоторой другой произвольной точке приложим силу Р2, от действия которой точка переместится на величину
- коэффициент пропорциональности. Теперь устраним действие силы Р1 и в некоторой другой произвольной точке приложим силу Р2, от действия которой точка переместится на величину 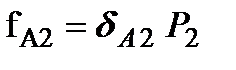 .
.
Очевидно, что коэффициенты пропорциональности 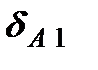 и
и 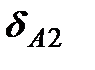 не равны между собой, так как силы Р1 и Р2 приложены в разных точках балки.
не равны между собой, так как силы Р1 и Р2 приложены в разных точках балки.
| P2 |
| fA2 |
| fA1 |
| P1 |
| A |
| P2 |
| A |
| fA1+fA2 |
| P1 |
| A |
Рис. 1.14. Принцип независимости действия сил
Рассмотрим теперь совместное действие сил Р1 и Р2. Приложим сначала силу Р1, а затем, не снимая ее, силу Р2. Тогда суммарное перемещение точки А можно определить по формуле 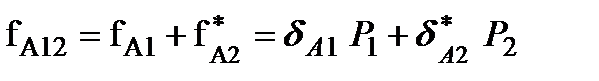 . Коэффициент
. Коэффициент 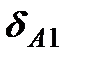 будет иметь тоже значение, т.к. сила Р1 была приложена к ненагруженной балке, коэффициент же пропорциональности для силы Р2 обозначен как
будет иметь тоже значение, т.к. сила Р1 была приложена к ненагруженной балке, коэффициент же пропорциональности для силы Р2 обозначен как 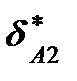 , т.к. сила Р2 приложена к системе, на которую уже действует сила Р1. Если коэффициенты
, т.к. сила Р2 приложена к системе, на которую уже действует сила Р1. Если коэффициенты 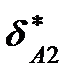 и
и 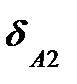 различны, то следует признать, что коэффициент
различны, то следует признать, что коэффициент 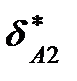 зависит от силы Р1 (даже имеющей нулевое значение), но это противоречит принятому предположению, о линейной зависимости перемещений от действующей силы. Следовательно,
зависит от силы Р1 (даже имеющей нулевое значение), но это противоречит принятому предположению, о линейной зависимости перемещений от действующей силы. Следовательно, 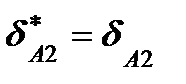 и тогда
и тогда 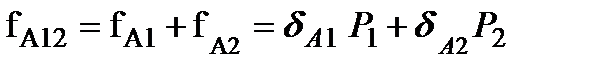 . Видно, что суммарное перемещение в точке А определяется как сумма перемещений от независимых действий сил Р1 и Р2.
. Видно, что суммарное перемещение в точке А определяется как сумма перемещений от независимых действий сил Р1 и Р2.
Таким образом, принцип независимости действия сил (принцип суперпозиции) сформулируем так: результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.
4. Закон Гука
При малых деформациях большинство тел можно считать линейно-упругими. Это означает, что при снятии внешней нагрузки тело полностью восстанавливает свою форму и размеры (идеальная упругость), и, кроме того, наблюдается линейная связь между силами P и смещениями D:
P=kD,
где k – коэффициент пропорциональности (жесткости), зависящий от вида и материала конструкции.
Действующие на упругое тело внешние силы совершают над ним работу. Эта работа, согласно закону сохранения механической энергии, переходит в потенциальную энергию упругой деформации. При сделанных выше допущениях и в предположении о квазистатическом приложении силы P потенциальная энергия легко определяется с помощью теоремы Клапейрона.
При медленном (квазистатическом) нагружении вся работа внешней нагрузки переходит в потенциальную энергию U:
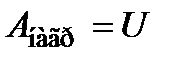 .
.
Рассмотрим пример работы под нагрузкой консольного стержня (рис. 1.15а) или двухопорной балки (рис. 1.15б), на которые действует сила P. При этом характерные точки обеих систем переместятся на величину D, а при дополнительном нагружении 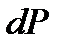 - на
- на 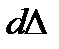 .
.
Рис. 1.15. К определению работы внешних сил
Элементарная работа равна (рис. 1.15в) 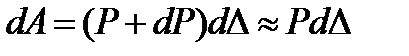 .
.
Полная работа, совершаемая силой Р, вызвавшей перемещение  , будет
, будет
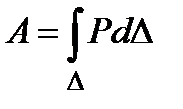 .
.
Этот интеграл представляет собой заштрихованную площадь диаграммы, и, значит, для линейно-упругой системы будет численно равен площади треугольника:
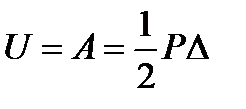 .
.
Данное равенство называется теоремой Клапейрона и имеет очень большое значение при исследовании перемещений различных упругих систем.
При действии на систему нескольких сил (n) теорема Клапейрона принимает вид:
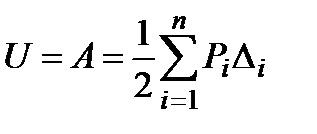 .
.
Дата добавления: 2015-09-07; просмотров: 2246;
