Разложение многочленов на простые сомножители.
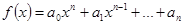 |
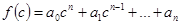 Пусть многочлен, коэффициенты которого a0, a1, …, an есть комплексные числа, переменная x может принимать любые комплексные значения. Число
Пусть многочлен, коэффициенты которого a0, a1, …, an есть комплексные числа, переменная x может принимать любые комплексные значения. Число
называется значением многочлена f(x) при x=c (или в точке x=c). Если f(c) = 0, то число x=c называют нулём многочлена f(x) или корнем уравнения f(x) = 0. Впрочем, часто говорят, что x=c является корнем многочлена f(x), если f(c) = 0.
При делении многочлена f(x) на многочлен первой степени x-c получают остаток, который может быть многочленом только нулевой степени. т.е. каким-то комплексным числом. В дальнейшем обозначаем его символом r.
Теорема (Безу).Остаток от деления многочлена f(x) на x-c равен значению f(c) многочлена f(x) для x=c.
Доказательство. В самом деле, пусть f(x) = (x - c)g(x) + r. Положим x=c. получим f(c) = (c - c)g(c) + r = r. Откуда и следует r = f(c).
Из теоремы Безу вытекает важное следствие: Для того, чтобы число с было нулём многочлена f(x), необходимо и достаточно, чтобы f(x) делился на х – с (т.е. r было равно 0).
Пусть f(x) есть многочлен степени n, n ³ 1, с комплексными или действительными коэффициентами.
Если x=c нуль этого полинома, то f(c) = 0 и f(x) делится на x-c. Может быть так. что f(x) делится не только на x-c, но и на (x-c)2, (x-c)3 и т.д. Во всяком случае найдётся такое натуральное число k, что f(x) будет делиться на (x-c)k, но уже не делится на (x-c)k+1.
Тогда
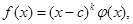 |
где многочлен j(x) уже не делится на (x-c), т.е. число c не является нулём j(x). Число k называют порядком кратности нуля с, а само с называют k-кратным нулём многочлена f(x). Если k=1, то нуль с называют простым. Справедлива следующая основная теорема алгебры: Всякий многочлен с комплексными коэффициентами степени не ниже первой (n ³ 1) имеет, по крайней мере, один нуль (действительный или комплексный).
Известно несколько способов доказательства этой теоремы, но все они используют материал и приёмы, нами ещё неизученные. Поэтому принимаем пока эту теорему без доказательства.
Теорема находит применения в разных областях науки. В частности, она служит базой для разложения многочлена с числовыми коэффициентами на множители. Эта одна из основных причин названия этой теоремы основной теоремой алгебры.
Итак, теорема гарантирует существование нуля c1 (действительного или комплексного) у многочлена f(x). Тогда многочлен f(x) может быть записан в виде f(x) = (x-c1) j(x). j(x) тоже есть многочлен степени n-1 с действительными или комплексными коэффициентами. По этой же теоремы j(x) имеет нуль с2, так что f(x) = (x-c1) j(x).
Продолжая этот процесс, мы придём после n «шагов» к представлению многочлена f(x) степени n в форме произведения n линейных множителей
(4) 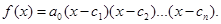
Произведение линейных множителей в (4) умножено на a0 (коэффициент старшего члена f(x)). Если бы это было другое число b, то раскрытие скобок, приведение подобных членов справа в (4) дало бы старший член многочлена f(x) в виде bxn, а не a0xn, чего быть не должно. Итак, b=a0.
Представление многочлена f(x) в форме произведения (4) является единственным с точностью до порядка сомножителей.
С учётом кратностей корней, группируя одинаковые сомножители, произведение (4) можно переписать в виде
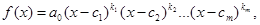 (5)
(5)
где k1 + k2 + … +km = n. В (5) уже предполагается, что все нули c1, c2, …, cm разные.
Рассмотрим теперь многочлены с действительными коэффициентами.
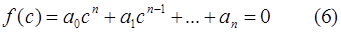
Пусть f(x) = a0xn + a1xn-1 + …+ an, где a0, a1, …, an – действительные числа.
Пусть x=c нуль (вообще говоря, комплексный), т.е.
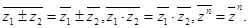 Возьмем сопряжение от обеих частей равенства (6). Учитывая действительность коэффициентов a0, a1, …, an и 0
Возьмем сопряжение от обеих частей равенства (6). Учитывая действительность коэффициентов a0, a1, …, an и 0
в правой части, справедливость равенств: (предлагаем проверить их самостоятельно), получим равенство
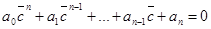 | |||
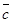 | |||
или f ( ) = 0.
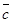
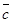 Итак, если комплексное число (не действительное!) c является нулём полинома f(x) с действительными коэффициентами, то сопряженное число тоже является его нулём. Очевидно кратности нулей с и совпадают.
Итак, если комплексное число (не действительное!) c является нулём полинома f(x) с действительными коэффициентами, то сопряженное число тоже является его нулём. Очевидно кратности нулей с и совпадают.
Как следствие, отсюда вытекает утверждение: многочлен f(x) делится на многочлен второй степени с действительными коэффициентами.
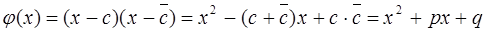
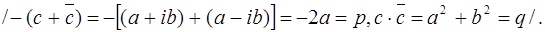 |
(7)
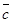 |
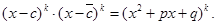 Если же с и являются k – кратными нулями f(x), то f(x) делится на
Если же с и являются k – кратными нулями f(x), то f(x) делится на
Из общего разложения (5) и фактов, касающихся многочленов с действительными коэффициентами, следует такой окончательный вывод.Всякий многочлен f(x) с действительными коэффициентами может быть представлен единственным образом (с точностью до порядка сомножителей) в виде произведения коэффициента а0 старшего члена, многочленов с действительными коэффициентами первой степени вида x-c, соответствующими действительным нулям f(x), многочленов второй степени с действительными коэффициентами вида (7), соответствующими парам сопряжённых комплексных нулей f(x).
Как следствие, всякий многочлен с действительными коэффициентами может быть разложен на множители с действительными коэффициентами первой и второй степени соответствующей кратности, т.е.
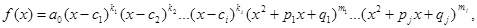 |
где k1 + k2 + … + kj + 2m1 + … + 2mj = n.
Дата добавления: 2015-10-05; просмотров: 860;
