Метод интегрирования по частям. Пусть функции и имеют непрерывные производные и Тогда имеет место равенство
Пусть функции 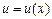 и
и 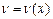 имеют непрерывные производные
имеют непрерывные производные  и
и 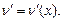 Тогда имеет место равенство
Тогда имеет место равенство
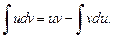 (19.20)
(19.20)
Формула (19.20) задает метод интегрирования по частям, согласно которому интегрирование выражения udv сводится к интегрированию выражения vdu Применение формулы (19.20) предполагает, что в правой части интеграл 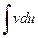 может быть вычислен легче, чем исходный. Формула (19.20) может быть записана также в виде
может быть вычислен легче, чем исходный. Формула (19.20) может быть записана также в виде
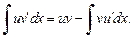
Рациональность вычисления некоторых интегралов зависит от того, как выбраны функции 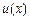 и
и 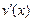 в заданном интеграле.
в заданном интеграле.
Формула интегрирования по частям может применяться неоднократно.
Рассмотрим следующие случаи:
1. Для вычисления интегралов вида 
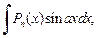
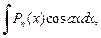 где
где 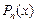 – многочлен степени n, в качестве функции
– многочлен степени n, в качестве функции 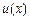 следует взять многочлен
следует взять многочлен 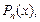 а в качестве
а в качестве 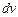 – одно из выражений
– одно из выражений 
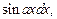
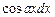 соответственно. При этом формулу интегрирования по частям следует применять n раз.
соответственно. При этом формулу интегрирования по частям следует применять n раз.
2. Для интегралов вида 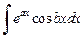 и
и 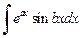 в качестве функции
в качестве функции 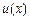 можно взять
можно взять 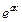 или
или 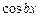
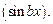 Формулу интегрирования по частям следует применить дважды, а затем из полученного равенства, как из уравнения, найти заданный интеграл.
Формулу интегрирования по частям следует применить дважды, а затем из полученного равенства, как из уравнения, найти заданный интеграл.
3. Для интегралов вида 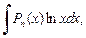
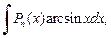
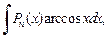
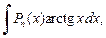
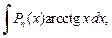
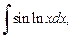
 в качестве u(x) берут функции lnx,
в качестве u(x) берут функции lnx, 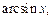
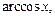
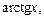
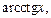
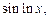
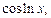 а в качестве dv – выражение
а в качестве dv – выражение 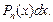 Такой подход используют и тогда, когда
Такой подход используют и тогда, когда 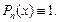
Во многих случаях подынтегральная функция зависит не только от аргумента, но и от натурального индекса n. Методом интегрирования по частям удается привести интеграл к интегралу такой же формы, но с меньшим значением индекса. После нескольких таких шагов приходят к интегралу, который можно вычислить с помощью таблицы. Такой метод интегрирования называют рекуррентным методом, а полученную формулу – рекуррентной формулой.
Пример 1. Методом интегрирования по частям найти неопределенный интеграл:
1) 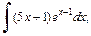 2)
2) 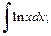 3)
3) 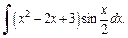
Решение. 1) Положим 
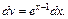 Тогда
Тогда 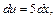
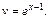 Используя формулу (19.20) интегрирования по частям, получаем:
Используя формулу (19.20) интегрирования по частям, получаем:
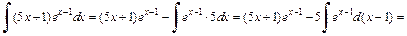
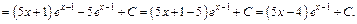
2) Применим формулу (19.20) интегрирования по частям:
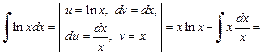
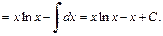
3) Положим 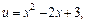
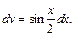 Тогда
Тогда 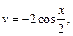
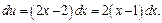 Применяя формулу (19.20), получаем:
Применяя формулу (19.20), получаем:
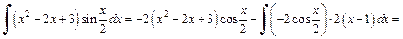
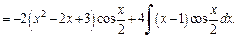
Применив формулу интегрирования по частям, понизили степень многочлена на единицу. Чтобы найти 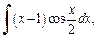 применим еще раз метод интегрирования по частям. Положим
применим еще раз метод интегрирования по частям. Положим 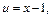
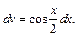 Тогда
Тогда 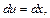
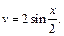 Получаем:
Получаем:
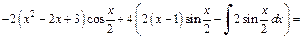
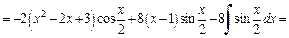
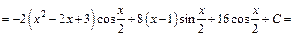
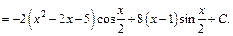
Пример 2. Методом интегрирования по частям найти неопределенный интеграл:
1) 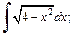 2)
2) 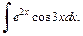
Решение.1)Интеграл 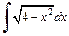 уже был вычислен в параграфе 19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки. Рассмотрим второй способ его вычисления, используя метод интегрирования по частям:
уже был вычислен в параграфе 19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки. Рассмотрим второй способ его вычисления, используя метод интегрирования по частям:
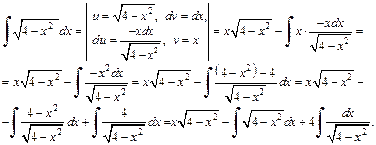
Вычислим последний интеграл, используя формулу (19.14) таблицы интегралов. Получим равенство

В правой части этого равенства получили исходный интеграл. Найдем его из уравнения: 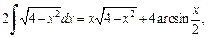 откуда получаем ответ:
откуда получаем ответ: 
2) Используя формулу интегрирования по частям дважды, получаем:

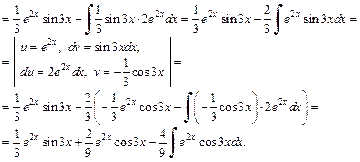
В результате получили равенство
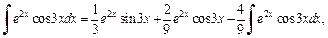
из которого находим:

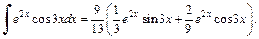
Приходим к ответу:
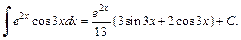
Пример 3. Найти неопределенный интеграл 
Решение. Используя формулу (19.20) интегрирования по частям, получаем:
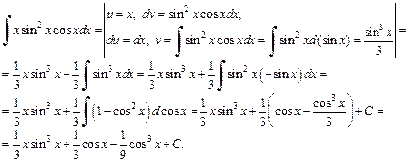
Пример 4.Найти неопределенный интеграл 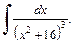
Решение. Преобразуем подынтегральное выражение:
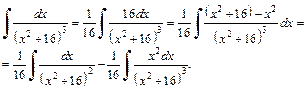
Последний интеграл вычислим, применяя формулу интегрирования по частям.
Полагаем 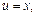
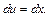
Если 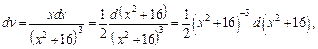 то
то
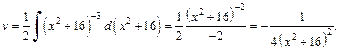
Тогда
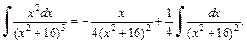
Таким образом, получаем выражение интеграла 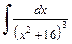 через интеграл
через интеграл 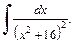

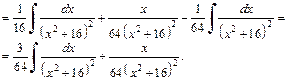
Вычисляем  аналогично первоначальному.
аналогично первоначальному.

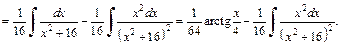
Для вычисления последнего интеграла применяем формулу интегрирования по частям:

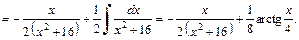
Имеем:
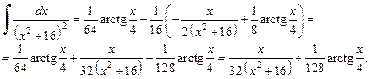
Получаем:
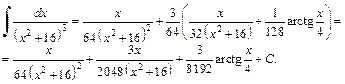
Пример 5. Получить рекуррентную формулу для вычисления интеграла 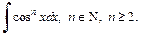 Используя ее, вычислить
Используя ее, вычислить 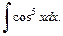
Решение. Обозначим 
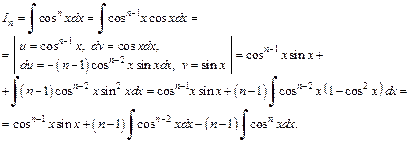
Мы получили:
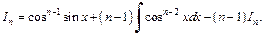
Выражаем:
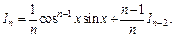
Это и есть рекуррентная формула, которая позволяет уменьшать показатель степени в подынтегральной функции до тех пор, пока не придем к интегралу 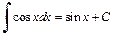 или
или 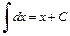 в зависимости от того, является ли n числом четным или нечетным.
в зависимости от того, является ли n числом четным или нечетным.
Используем ее для вычисления 
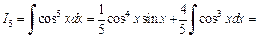
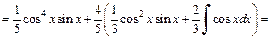

Дата добавления: 2015-09-29; просмотров: 1883;
