Матричная передаточная функция многомерной системы.

Определение. Матричной ПФ линейной многомерной системы W(p) называется функция, которая связывает преобразования Лапласа выхода 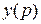и входа u(p)этой предварительно невозбужденной системы,

. (*)

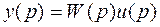Это есть уравнение «вход - выход» многомерной системы в изображениях.

Поставим задачу выразить матричную ПФ с помощью матриц A, B, C, описывающих модель в переменных состояния.

Для предварительно возбужденной системы l - вектор выхода c учетом выражений 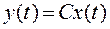и

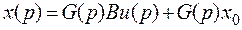
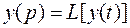= CL[x (t)]= ,

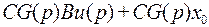где u(p) =L[u(t)] – r-вектор входа.

При х₀=0 (система предварительно невозбуждена)

y(p) = CG(p)B u(p).

Следовательно,

.

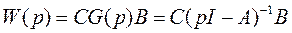Матричная передаточная функция W(p) есть матрица 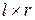. Если l=r=1, то матричная ПФ вырождается в скалярную ПФ

.

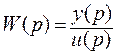В символическом виде матричная ПФ

, ,

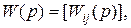
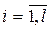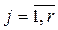где 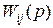- (i,j)-й элемент (скалярная функция) матричной ПФ, называемый скалярной ПФ.

Выясним смысл скалярных передаточных функций. Представим выражение ( * ) 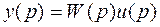в развернутом виде:

.

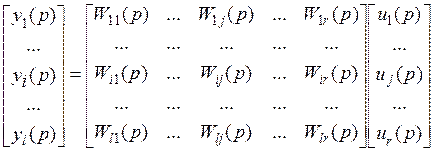Отсюда преобразование Лапласа i-го выхода

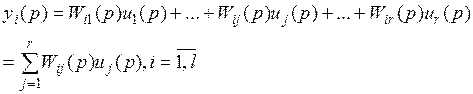(3)

Если мы положим нулю все входы 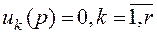, , 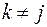кроме j –го входа 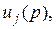то

,

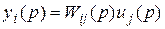Тогда можем найти выражение для скалярной ПФ в следующем виде

.

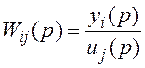Вывод. Скалярная передаточная функция – это отношение изображений по Лапласу i-го выходного и j-го входного сигналов предварительно невозбужденной системы при условии, что все остальные входные сигналы, кроме j-го, отсутствуют.

Структурная схема системы, являющаяся графическим отображением

уравнения (3)

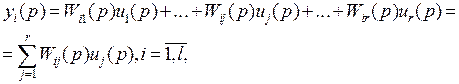
представляет собой блок-схему и называется динамической структурной схемой многомерной системы.

Построим динамическую структурную схему (рисунок ниже) для двумерной системы (l= r=2), описываемой уравнениями

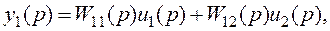
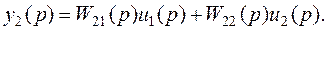
При этом используем элементы, которые применялись при построении структурных схем одномерных систем.

Скалярную ПФ можно представить как:

, , .

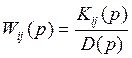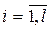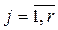Здесь 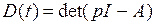- характеристический многочлен системы, K_ij(p) –многочлен от p.

Заметим, что матричная ПФ представляет собой преобразование Лапласа от матричной весовой функции: 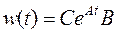. Действительно,

.

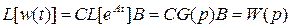Отсюда матричная весовая функция представляет собой обратное преобразование Лапласа от матричной ПФ,

.

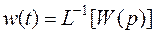Команда Matlab: [Num,Den]=ss2tf(A,B,C,D)

Определение ПФ по известным A,B,C,D называют переходом от описания системы в переменных состояния к описанию «вход - выход».

Если подставить в выражение для матричной ПФ 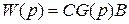выражение для резольвенты

,

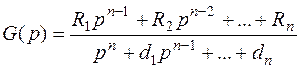полученное в предыдущем параграфе, то нетрудно найти, что

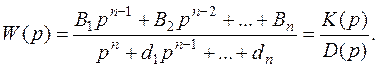
Здесь 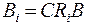, 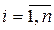- постоянные ( 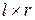) матрицы. Если r=l=1, то матричный полином K(p) вырождается в скалярный полином

,

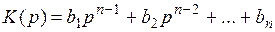где b_i – постоянные коэффициенты.