Розв’язування систем лінійних рівнянь за формулами Крамера.
Розглянемо систему трьох лінійних рівнянь з трьома невідомими:
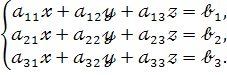
 Обчислимо визначник
Обчислимо визначник

Якщо 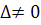 , система має єдиний розв’язок, який знаходиться за формулами Крамера :
, система має єдиний розв’язок, який знаходиться за формулами Крамера :
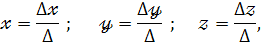
де
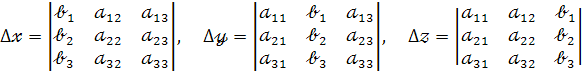
Якщо 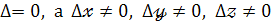 - система несумісна.
- система несумісна.
Якщо 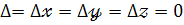 – система невизначена.
– система невизначена.
Приклад 9. Розв’язати систему рівнянь за формулами Крамера :
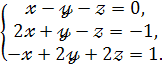
Розв’язання.
Знаходимо визначники системи : 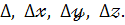
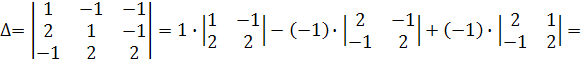
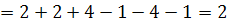
Визначник відмінений від нуля, отже можна знаходити розв’язок системи за формулами Крамера.
Знаходимо 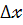 . Його одержуємо шляхом заміни першого стовпця стовпцем вільних членів системи :
. Його одержуємо шляхом заміни першого стовпця стовпцем вільних членів системи :
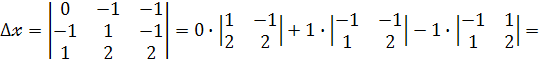
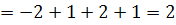
Знаходимо визначник 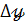 . Його одержуємо із
. Його одержуємо із  шляхом заміни другого совпця стовпцем вільних членів системи :
шляхом заміни другого совпця стовпцем вільних членів системи :
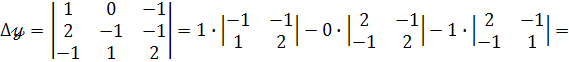
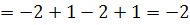
Визначник 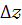 одержуємо із визначника
одержуємо із визначника  шляхом заміни третього стовпця стовпцем вільних членів.
шляхом заміни третього стовпця стовпцем вільних членів.
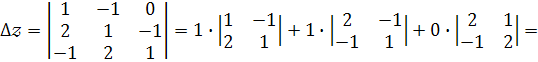
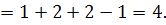
За формулами Крамера маємо :
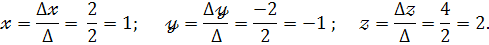
Відповідь : 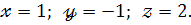
Дата добавления: 2015-06-27; просмотров: 1320;
