Лекция 3. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Метрологические характеристики прибора – это те, которые непосредственно связаны с его основным назначением – производством измерений. В эти характеристики входят пределы измерения, основная и дополнительные погрешности и класс точности.
Верхний и нижний пределы измерения ограничивают область (диапазон) использования прибора и поэтому представляют собой наиболее важную его характеристику. Чаще всего нижним пределом измерения прибора является нуль, что означает что, измеряемая величина, как таковая, отсутствует. Однако, это не всегда так. Иногда нуль располагается между верхним и нижним пределами и делит значения измеряемой величины на положительные и отрицательные. Пример – шкала термометра. Диапазон измерения
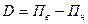 , (3.1)
, (3.1)
где 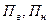 – верхний и нижний пределы измерения. При
– верхний и нижний пределы измерения. При 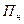 = 0,
= 0,
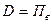 , (3.2)
, (3.2)
если же 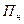 < 0, то из формулы (3.1) вытекает, что
< 0, то из формулы (3.1) вытекает, что
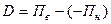 или
или 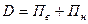 (3.3)
(3.3)
При оценке точности прибора, его погрешность экспериментальным путем устанавливают у всех числовых отметок его шкалы. Пусть, показания образцового и поверяемого манометров на рис. 2.1 приняли значения, приведенные на таблице 3.1
Таблица 3.1. Результаты поверки манометра
Показания поверяемого прибора, 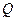 , МПа , МПа
| ||||||
Показания образцового прибора, 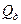 , МПа , МПа
| 0.97 | 2.02 | 2.94 | 3.98 | 5.05 | |
Ошибка поверяемого прибора, 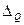 , МПа (форм. (1.6)) , МПа (форм. (1.6))
| 0.03 | -0.02 | 0.06 | 0.02 | -0.05 |
У разных числовых отметок погрешности поверяемого прибора приняли разные значения, причем не только по величине но и по знаку. Если принимать в расчет только абсолютную величину этих погрешностей, то максимальным значением – 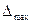 = 0.06 МПа – характеризуется погрешность у числовой отметки 3 МПа. Значение максимальной абсолютной погрешности прибора, отнесенное к его диапазону измерения, называется приведенной погрешностью этого прибора.
= 0.06 МПа – характеризуется погрешность у числовой отметки 3 МПа. Значение максимальной абсолютной погрешности прибора, отнесенное к его диапазону измерения, называется приведенной погрешностью этого прибора.
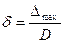 , или (с учетом (3.2))
, или (с учетом (3.2)) 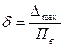 (3.4)
(3.4)
Гостированное значение приведенной погрешности называется классом точности прибора. В стандарте задан параметрический ряд классов точности в процентах. Это: 4, 2.5, 1.5, 1, 0.4, 0.25, 0.15, 0.1, 0.04, 0.025… и т.д. Класс точности 4%, является предельно-допустимым (значения хуже 4% допускаются лишь в виде исключения). В общем случае за класс точности принимают ближайшее большее по отношению к приведенной погрешности значение параметрического ряда. Класс точности обозначается на циферблате прибора, либо указывается в его паспорте.
В примере (таблица 3.1) при диапазоне 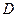 = 5 МПа приведенная погрешность манометра равна
= 5 МПа приведенная погрешность манометра равна 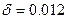 или 1.2 % Из двух ближайших значений параметрического ряда (1 и 1.5 ), прибору присваивается класс точности
или 1.2 % Из двух ближайших значений параметрического ряда (1 и 1.5 ), прибору присваивается класс точности 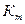 = 1.5 %
= 1.5 %
Максимально-допустимое при нормальных условиях измерения значение абсолютной погрешности прибора называется его основной погрешностью:
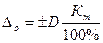 , или
, или 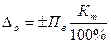 (3.5)
(3.5)
Т. к. 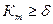 , то и
, то и 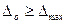 , (3.6)
, (3.6)
т. е. основная погрешность прибора не должна быть меньше наибольшей погрешности, полученной экспериментальным путем (в рассмотренном примере 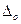 = 0.075 МПа)
= 0.075 МПа)
В случаях, когда истинные значения погрешностей прибора имеют особо важное значение, при производстве измерений данным прибором пользуются его градуировочной таблицей , в которой против каждой числовой отметки шкалы указано значение и знак соответствующей погрешности (как в таблице 3.1). В большинстве же случаев практически достаточно считать, что в любой точке шкалы при нормальных условиях измерения погрешность прибора равна его основной погрешности. Это дает уверенность в том, что истинная точность прибора не будет завышена.
При таком подходе (при условном постоянстве абсолютной погрешности) относительная погрешность измерения прибором (формула 1.7) приводится к виду
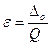 , (3.7)
, (3.7)
Таблица 3.2. Значения 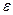 у числовых отметок манометра при
у числовых отметок манометра при 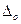 = 0.075 МПа
= 0.075 МПа
Числовые отметки, 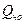 , МПа , МПа
| ||||||
Относительные ошибки, 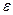
| - | 0.075 | 0.038 | 0.025 | 0.019 | 0.015 |
Из таблицы 3.2 (продолжение примера, данного в таблице 3.1) видно, что относительные погрешности максимальны на наименьшей числовой отметке и минимальны (равны классу точности) на наибольшей отметке. Это следует из формулы (3.7). Пример подтверждает правило, согласно которому разовые измерения желательно проводить в верхней трети шкалы. Это обеспечит наибольшую точность измерений.
Соответственно, ожидаемое значение измеряемой величины должно быть
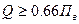 . (3.8)
. (3.8)
Наоборот, при выборе прибора для разовых измерений величины 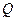 , его верхний предел
, его верхний предел 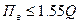 . (3.9)
. (3.9)
Требуемый класс точности определяют по заданной максимально допустимой относительной погрешности 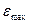 , принимая
, принимая 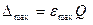 (3.10)
(3.10)
При выборе метрологических характеристик прибора непрерывного действиянеобходимо знать ожидаемый диапазон измеряемой величины от 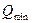 до
до 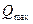 и наибольшую допустимую относительную погрешность
и наибольшую допустимую относительную погрешность 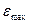 . Тогда стремятся к тому, чтобы соблюдались соотношения
. Тогда стремятся к тому, чтобы соблюдались соотношения 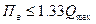 , (3.11)
, (3.11)
Максимальная абсолютная погрешность
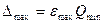 , (3.12)
, (3.12)
и приведенная погрешность 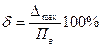 . (3.13)
. (3.13)
По приведенной погрешности из параметрического ряда выбирают соответствующий класс точности. Необходимо подчеркнуть, что при выборе приборав соответствии с заданной целью измерения, из ряда следует брать не ближайшее большее значение (как приоценкеточности прибора – см выше, формулы (3.4) – (3.6)), а наоборот, – ближайшее меньшее значение. В противном случае не выполняется требование непревышения заданного максимума относительной погрешности 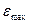 .
.
Для примера в таблице 3.3 заданы требования к исходным параметрам расхода
Таблица 3.3. Выбор метрологических характеристик бурового расходомера
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Минимальный расход, 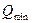 , л/с , л/с
| ||
Максимальный расход, 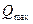 , л/с , л/с
| ||
Максимальная относительная погрешность, 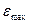
| 0.1 | |
| Результаты расчетов | ||
Верхний предел измерения расходомера, 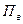 , л/с , л/с
| (3.11) | |
Максимальная абсолютная погрешность, 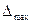 , л/с , л/с
| 0.5 | (3.12) |
Приведенная погрешность, 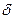 , % , %
| 1.25 | (3.13) |
Класс точности, 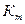 ,% ,%
| (из параметрического ряда) | |
Основная погрешность, 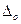 , л/с , л/с
| 0.4 | (3.5) |
промывочной жидкости и по ним найдены метрологические характеристики расходомера.
Чем выше класс точности прибора, тем он дороже, сложнее в эксплуатации и обслуживании, чаще требует поверок и ремонтов. Поэтому надо стремиться использовать приборы возможно более низких классов точности, но при этом достигать необходимой точности измерений. Это достигается применением многопредельных приборов.
Многопредельные приборы имеют два или более диапазонов измерения и один – невысокий – класс точности. Каждый диапазон имеет свою основную погрешность, величина которой тем ниже, чем ниже его верхний предел. Нижний диапазон применяется для малых значений измеряемой величины, верхний – для больших Для перехода с одного диапазона на другой имеется специальный переключатель диапазонов (рис. 8.4) . Многопредельные приборы позволяют сохранять заданную точность измерений (максимальную относительную погрешность) на всех диапазонах. Для расчета метрологических характеристик таких приборов задаются не только 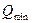 ,
, 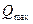 и
и 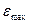 , но и желаемым невысоким классом точности
, но и желаемым невысоким классом точности 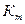 . Вначале рассчитывают 1-й диапазон
. Вначале рассчитывают 1-й диапазон 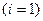 с самым малым верхним пределом. Принимают
с самым малым верхним пределом. Принимают 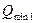 =
= 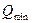 (3.14)
(3.14)
По формуле (3.12) принимающей вид 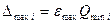 , (3.15)
, (3.15)
вычисляют 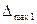 и принимают это значение за основную погрешность на данном диапазоне
и принимают это значение за основную погрешность на данном диапазоне
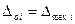 . (3.16)
. (3.16)
Преобразуя формулу (3.5), получают значение верхнего предела измерения
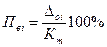 . (3.17)
. (3.17)
Принимают верхний предел первого диапазона за минимум измеряемой величины на втором диапазоне 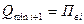 . (3.18)
. (3.18)
Далее определяют 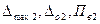 , снова применяя соответственно формулы (3.15), (3.16), (3.17). Если найденное значение
, снова применяя соответственно формулы (3.15), (3.16), (3.17). Если найденное значение 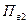 удовлетворяет условию
удовлетворяет условию
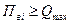 , (3.19)
, (3.19)
то выбирают двухдиапазонный прибор, иначе рассчитывают третий диапазон и т. д.
Пример. Для условий предыдущего примера ( 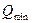 = 5 л/с,
= 5 л/с, 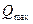 = 30 л/с,
= 30 л/с, 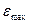 = 0.1), рассчитан многопредельный расходомер с классом точности 4% (таблица 3.4)
= 0.1), рассчитан многопредельный расходомер с классом точности 4% (таблица 3.4)
Таблица 3.4. Расчет многопредельного расходомера с классом точности 4%
| Параметр, символ, единица | Значение | Формула |
| Первый диапазон измерения | ||
Минимальный расход, 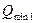 , л/с , л/с
| (3.14) | |
Максимальная абсолютная погрешность, 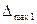 , л/с , л/с
| 0.5 | (3.15) |
Основная погрешность, 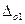 , л/с , л/с
| 0.5 | (3.16) |
Верхний предел измерения расходомера, 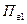 , л/с , л/с
| (3.17) | |
| Второй диапазон измерения | ||
Минимальный расход, 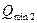 , л/с , л/с
| (3.18) | |
Максимальная абсолютная погрешность, 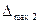 , л/с , л/с
| 1.2 | (3.15) |
Основная погрешность, 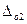 , л/с , л/с
| 1.2 | (3.16) |
Верхний предел измерения расходомера, 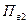 , л/с , л/с
| 30* | (3.17) |
* Удовлетворяет условию (3.19), поэтому прибор остается двухдиапазонным
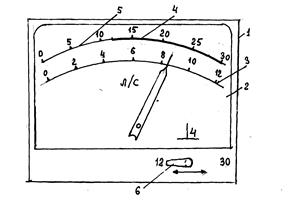
Рис.3.1 Расходомер с двухпредельной шкалой
1 – корпус показывающего прибора; 2 – циферблат; 3 – шкала нижнего диапазона; 4 – рабочая часть шкалы верхнего диапазона; 5 – нерабочая (относящаяся к нижнему диапазону) часть шкалы верхнего диапазона; 6 – переключатель диапазонов
На работу измерительного прибора и, в частности, на его точность, сильное влияние оказывают факторы внешней среды. К ним относятся климатические факторы, механические факторы, а для электрических приборов также и параметры питающей сети. Температура окружающего воздуха, его влажность, атмосферное давление относятся к климатическим факторам; наличие вибраций, сотрясений; ударов, пыли и брызгов – к механическим факторам; питающая сеть характеризуется напряжением и частотой.
Существуют так называемые нормальные условия измерения. Нормальными условиями измерения называют такие, при которых все влияющие факторы внешней среды находятся у значений (или в пределах некоторых интервалов значений), которые согласно паспорту данного прибора считаются нормальными. Так, нормальной температурой для большинства приборов, включая приборы контроля режима бурения, считается 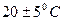 ; нормальная влажность – до 90% (если температура не превышает
; нормальная влажность – до 90% (если температура не превышает 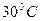 ); нормальное давление – 765 мм ртутного столба. В условиях, опасных по вибрациям, пыли и брызгам, приборы должны иметь соответствующую защиту. Напряжение питания у разных электрических приборов может быть разным – от 1.5 В до 380 В, поэтому нормальным считается напряжение, составляющее 100
); нормальное давление – 765 мм ртутного столба. В условиях, опасных по вибрациям, пыли и брызгам, приборы должны иметь соответствующую защиту. Напряжение питания у разных электрических приборов может быть разным – от 1.5 В до 380 В, поэтому нормальным считается напряжение, составляющее 100 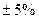 % от значения, указанного в паспорте прибора. Нормальная частота питающей сети на территории СНГ равна 50
% от значения, указанного в паспорте прибора. Нормальная частота питающей сети на территории СНГ равна 50 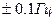 .
.
Выше указывалось, что при нормальных условиях измерения погрешность прибора не должна превышать значение его основной погрешности 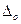 . Если же какой-либо фактор внешней среды от нормы отклонился, то в этом случае, кроме основной погрешности, прибор имеет право еще и на дополнительную погрешность
. Если же какой-либо фактор внешней среды от нормы отклонился, то в этом случае, кроме основной погрешности, прибор имеет право еще и на дополнительную погрешность 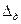 , тем большую, чем больше отклонение. Тогда общая допустимая погрешность прибора равна
, тем большую, чем больше отклонение. Тогда общая допустимая погрешность прибора равна
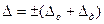 . (3.20)
. (3.20)
Дополнительная погрешность в этой формуле зависит от всех влияющих факторов, рассматриваемых вместе. Дополнительная погрешность по какому-то одному влияющему факторуА 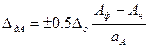 . (3.21)
. (3.21)
В этой формуле 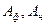 –фактическое и нормальное значения влияющего фактора, а
–фактическое и нормальное значения влияющего фактора, а
Таблица 3.5. Значения стандартного отклонения 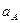
| Наименование влияющего фактора | Стандартное отклонение 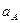
|
Температура окружающего воздуха, 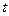 , градусов , градусов
| |
Напряжение питающей сети, 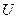 , % от номинального , % от номинального
| |
Частота питающей сети, 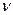 , Гц , Гц
|
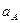 – такое отклонение фактора от нормального значения, которое вызывает рост погрешности на
– такое отклонение фактора от нормального значения, которое вызывает рост погрешности на 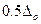 . Значения
. Значения 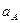 приводятся в стандартах (таблица 3.5).
приводятся в стандартах (таблица 3.5).
После установления дополнительных погрешностей, по всем, отклонившимся от нормальных условий факторам 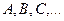 , ( т. е.
, ( т. е. 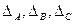 …), суммарная
…), суммарная
Таблица 3.6. Общая допустимая погрешность электрического манометра
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Основная погрешность, 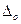 , МПа , МПа
| 0.1 | |
Нормальная температура, 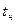 , град , град
| ||
Фактическая температура, 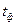 , град , град
| ||
Стандартное отклонение температуры от нормальной, 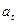 , град , град
| ||
Нормальная частота сети, 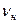 , Гц , Гц
| ||
Фактическая частота сети, 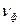 , Гц , Гц
| ||
Стандартное отклонение частоты от нормальной, 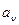 , Гц , Гц
| ||
| Результаты расчетов | ||
Дополнительная погрешность по температуре, 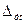 , МПа , МПа
| 0.1 | (3.21) |
Дополнительная погрешность по частоте, 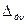 , МПа , МПа
| 0.15 | (3.21) |
Суммарная дополнительная погрешность, 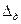 , МПа , МПа
| 0.18 | (3.22) |
Общая допустимая погрешность, 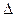 , МПа , МПа
| 0.28 | (3.20) |
дополнительная погрешность определяется как
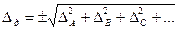 (3.22)
(3.22)
Пример нахождения общей допустимой погрешности манометра при отклонениях влияющих факторов внешней среды от нормальных условий приведен в таблице 3.6
Все измерительные приборы должны периодически – с периодичностью, указанной в их паспорте – проходить поверку. Часто такой период равняется одному году. Цель поверки – убедиться, что за очередной период эксплуатации основная и дополнительные погрешности прибора не вышли за допустимые пределы.
По отношению к поверке все приборы делятся на три группы: эталоны, образцовые приборы и рабочие приборы. Эталономназывается измерительное средство, обладающее наивысшей точностью, достижимой на данном этапе развития науки и техники. Так, если 50 лет назад эталоном метра было расстояние между насечками на платиноиридиевом стержне, то в наше время эталон метра считается равным 1650763.73 длин волны излучения, соответствующего оранжевой линии в спектре криптона-86. Абсолютная погрешность числа равна половине его последнего знака, т. е, в случае указанного числа длин волн – это 0.005 от длины одной волны (число заканчивается сотыми) Отсюда относительная погрешность (формула(1.7)) эталона метра 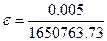 =3*
=3* 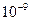
Существуют первичные, вторичные и третичные эталоны. Каждая основная единица системы СИ имеет свой эталон, хранящийся в Бюро мер и весов в Париже. Все государства, использующие систему СИ имеют одну копию этого эталона в качестве своего первичного-государственного эталона данной единицы. По первичному эталону, как по образцу, выполняется несколько вторичных эталонов, по ним – гораздо большее число третичных эталонов. Первичные эталоны постоянно находится на хранении в специальной организации (в России – это Институт метрологии им. Д.И. Менделеева в Санкт Петербурге). Все влияющие факторы внешней среды в помещении хранения строго стабилизированы. Третичные эталоны хранятся в крупных городах. По первичным эталонам периодически проходят поверку соответствующие вторичные эталоны, по вторичным – третичные эталоны, по третичным так называемые образцовые приборы.
Образцовые приборы служат для поверки, и градуировки рабочих приборов, используемых на различных производствах для контроля применяемой технологии. Поверять одни рабочие приборы с помощью других (пусть более точных) рабочих приборов запрещено. Используемый для поверки образцовый прибор должен иметь тот же диапазон измерения, что и поверяемый прибор. Основная погрешность образцового прибора должна быть не более 0.1 от основной погрешности поверяемого прибора (в исключительных случаях это соотношение может быть повышено до 0.33)
Процедура поверки заключается в том, что рабочий и образцовый приборы помещаются в одну и ту же измерительную магистраль (см., например рис. 2.1) поверочной установки. Поверка производится на всех числовых отметках (как в таблице 3.1), причем по формуле (1.6) определяется 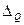 . Числовые отметки вначале проходятся путем повышения измеряемого параметра, а потом – путем его снижения. Циклов повышения-снижения проводится не менее трех, и по всем циклам, рассматриваемым совместно, вычисляют максимальное по абсолютной величине значение абсолютной погрешности прибора
. Числовые отметки вначале проходятся путем повышения измеряемого параметра, а потом – путем его снижения. Циклов повышения-снижения проводится не менее трех, и по всем циклам, рассматриваемым совместно, вычисляют максимальное по абсолютной величине значение абсолютной погрешности прибора 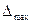 .
.
Если проверяется основная погрешность прибора, то ее вычисленное по формуле (3.5) значение сравнивают с 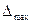 , процедура определения которого должна быть проведенапри нормальных значениях всех факторов внешней среды. Необходимо, чтобы по абсолютной величине
, процедура определения которого должна быть проведенапри нормальных значениях всех факторов внешней среды. Необходимо, чтобы по абсолютной величине 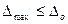 . (3.23)
. (3.23)
Если проводится поверка дополнительной погрешности, то прибор помещают в условия, когда рассматриваемый фактор 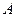 внешней среды выходит за рамки нормальных значений (при проверке температурной погрешности прибор помещают в термостат для повышения либо снижения окружающей температуры) Образцовый же прибор оставляют в нормальных условиях. Так определяют
внешней среды выходит за рамки нормальных значений (при проверке температурной погрешности прибор помещают в термостат для повышения либо снижения окружающей температуры) Образцовый же прибор оставляют в нормальных условиях. Так определяют 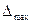 . Необходимо, чтобы
. Необходимо, чтобы
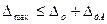 , (3.24)
, (3.24)
где 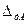 – допустимая дополнительная погрешность, рассчитанная по формуле (3.21)
– допустимая дополнительная погрешность, рассчитанная по формуле (3.21)
Если условия (3.23) и (3.24) соблюдены, то прибор выдержал поверку, и в его паспорте ставят соответствующую отметку с разрешением использования в течение следующего межповерочного срока. В противном случае прибор считается неисправным и его использование запрещается. Тогда он либо сдается на юстирование ( ремонт с целью повышения точности ), либо списывается.
Рекомендуемая литература: 1. с. 61-72.
Контрольные вопросы
1. Что такое пределы измерения прибора?
2. Что такое класс точности и как его находят?
3. Как выбрать прибор, если известны требования к результатам измерений?
4. Что такое основная и дополнительная погрешности измерительного прибора?
5. Как классифицируют измерительные средства, участвующие в поверке?
Дата добавления: 2015-06-27; просмотров: 7639;
