Структурный подход к измерению информации

В рамках структурного подхода выделяют три меры информации:

· геометрическая.Определяет максимально возможное количество информации в заданных объемах. Мера может быть использована для определения информационной емкости памяти компьютера;

· комбинаторная. Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Комбинаторная мера может использоваться для оценки информационных возможностей некоторого системы кодирования;

· аддитивная, или мера Хартли.

Геометрическая мера

Определяет максимально возможное количество информации в заданных объемах. Единица измерения – информационный элемент. Мера может быть использована для определения информационной емкости памяти компьютера. В этом случае в качестве информационного элемента выступает минимальная единица хранения – бит. Список самых распространенных более крупных единиц и соотношение между ними приведено ниже:

8 бит = 1 байт (сокращенно б или Б),

1024 Б = 1 килобайт (сокращенно Кб или К),

1024 К = 1 мегабайт (сокращенно Мб или М),

1024 М = 1 гигабайт (сокращенно Гб или Г).

Тогда, например, объем винчестера – 3 гигабайта; объем основной памяти компьютера – 32 мегабайта и т.д.

Пример 1. Пусть сообщение

5555 6666 888888

закодировано одним из специальных методов эффективного кодирования – кодирование повторений – и имеет вид:

5(4) 6(4) 8(6) .

Требуется измерить информацию в исходном и закодированном сообщениях геометрической мерой и оценить эффективность кодирования.

В качестве информационного элемента зададимся символом сообщения. Тогда:

I(исх.) = l(исх.) = 14 символов;

I(закод.) = l(закод.) = 12 символов,

где I(исх.), I(закод.) – количества информации, соответственно, в исходном и закодированном сообщениях;

l(исх.), l(закод.) – длины (объемы) тех же сообщений, соответственно.

Эффект кодирования определяется как разница между I(исх.) и I(закод.) и составляет 2 символа.

Очевидно, геометрическая мера не учитывает, какими символами заполнено сообщение. Так, одинаковыми по количеству информации, измеренной геометрической мерой, являются, например, сообщения «компьютер» и «программа»; а также 346 и 10В.

Комбинаторная мера

Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Использует типы комбинаций элементов и соответствующие математические соотношения, которые приводятся в одном из разделов дискретной математики – комбинаторике.

Комбинаторная мера может использоваться для оценки информационных возможностей некоторого автомата, который способен генерировать дискретные сигналы (сообщения) в соответствии с определенным правилом комбинаторики. Пусть, например, есть автомат, формирующий двузначные десятичные целые положительные числа (исходное множество информационных элементов {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}). В соответствии с положениями комбинаторики, данный автомат генерирует размещения (различаются числа, например, 34 и 43) из 10 элементов (используются 10 цифр) по 2 (по условию задачи, формируются двузначные числа) с повторениями (очевидно, возможны числа, состоящие из одинаковых цифр, например, 33). Тогда можно оценить, сколько различных сообщений (двузначных чисел) может сформировать автомат, иначе говоря, можно оценить информационную емкость данного устройства: Рп(102) = 102 = 100.

Комбинаторная мера используется для определения возможностей кодирующих систем, которые широко используются в информационной технике.

Пример 1. Определить емкость ASCII-кода, представленного в двоичной или шестнадцатеричной системе счисления.

ASCII-код – это сообщение, которое формируется как размещение с повторениями:

· для двоичного представления – из информационных элементов {0, 1}, сообщение длиной (объемом) 8 символов;

· для шестнадцатеричного представления – из информационных элементов {0, 1, 2, …., А, В, С, …. F}, сообщение длиной (объемом) 2 символа.

Тогда в соответствии с положениями комбинаторики:

I(двоичное) = РП(28) = 28 = 256;

I(шестнадцатеричное) = РП(162) = 162 = 256,

где I(двоичное), I(шестнадцатеричное) – количества информации, соответственно, для двоичного и шестнадцатеричного представления ASCII-кода.

Таким образом, емкость ASCII-кода для двоичного и шестнадцатеричного представления одинакова и равна 256.

Следует отметить, что все коды постоянной длины формируются по правилам комбинаторики или их комбинациям.

В случае, когда сообщения формируются как размещения с повторениями из элементов алфавита мощности h и известно количество сообщений М, можно определить требуемый объем сообщения (т.е. его длину l) для того, чтобы в этом объеме представить все сообщения: l = log h М .

Например, есть 4 сообщения – a, b, c, d. Выполняется двоичное кодирование этих сообщений кодом постоянной длины. Для этого требуются 2 двоичных разряда. В самом деле: l = log 2 4 = 2.

Очевидно, комбинаторная мера является развитием геометрической меры, так как помимо длины сообщения учитывает объем исходного алфавита и правила, по которым из его символов строятся сообщения.

Особенностью комбинаторной меры является то, что ею измеряется информация не конкретного сообщения, а всего множества сообщений, которые могут быть получены.

Единицей измерения информации в комбинаторной мере является число комбинаций информационных элементов.

Введение Информация Свойства информации Сигнал Системы счисления Кодирование сигнала Измерение информации Структурный подход Геометрическая мера Комбинаторная мера Положения комбинаторики Аддитивная мера Статистический подход Семантический подход Качество информации Компьютер Информационный процесс

Положения комбинаторики, используемые в измерении информации   Комбинаторика – раздел дискретной математики, изучающий способы формирования подмножеств из элементов исходных множеств: в соответствии с положениями комбинаторики, из конечного счетного множества элементов мощности h можно сформировать следующие простейшие виды комбинаций элементов:   1. сочетания С, когда элементы исходного множества группируются в подмножества одинаковой мощности l такие, что элементы в них различаются составом, а порядок элементов безразличен. Например, пусть исходное множество содержит некоторые символы латинского алфавита и имеет вид - {a,b,c} (h=3). Тогда можно сформировать следующие подмножества мощности 2 по правилу сочетаний: {a,b}, {a,c}, {b,c}. В соответствии с определением сочетания множества {a,b} и {b,a} являются идентичными и не формируются.   2. перестановки П, когда элементы исходного множества группируются в подмножества одинаковой мощности l (l = h) такие, что элементы в них различаются только порядком. Например, из приведенного выше исходного множества можно сформировать следующие подмножества по правилу перестановок: {a,b,c}, {b,c,a}, {a,c,b}, {b,a,c}, {c,a,b}, {c,b,a}.   3. размещения Р, когда элементы исходного множества группируются в подмножества одинаковой мощности l, такие, что элементы в них различаются и составом, и порядком. Например, из приведенного выше исходного множества можно сформировать следующие подмножества по правилу размещения: {a,b}, {b,a}, {a,c}, {c,a}, {b,c}, {c,b}.   Помимо указанных способов, возможны их модификации, когда элементы в результирующих подмножествах могут повторяться (тогда указанные соотношения между l и h не выполняются). В этом случае говорят о группировании элементов с повторениями, причем для перестановки указывается, сколько раз повторяется в результирующем подмножестве каждый элемент. Так, получаем следующие результаты для примера исходного множества: 1. сочетания по 2 элемента с повторениями (Сп): {a,b}, {a,c}, {b,c}, {a,a}, {b,b}, {c,c}; 2. перестановки с повторениями (Пп) (число повторений задано: ra = 2, rb = 1, rc = 1, где ri – число повторений элемента i): {a,a,b,c}, {a,a,c,b}, {a,b,a,c}, {a,b,c,a}, {a,c,a,b}, {a,c,b,a}, {b,c,a,a}, {b,a,c,a}, {b,a,a,c}, {c,a,a,b}, {c,a,b,a}, {c,b,a,a}; 3. размещения по 2 элемента с повторениями (Рп): {a,b}, {b,a}, {a,c}, {c,a}, {b,c}, {c,b}, {a,a}, {b,b}, {c,c}.   Комбинаторика позволяет для каждого из указанных способов группирования элементов рассчитывать число получаемых подмножеств: 1. число сочетаний из h элементов по l без повторений С(hl ): 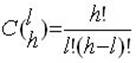2. число сочетаний из h элементов по l с повторениями Сп(hl ): 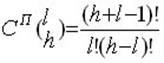3. число перестановок из h элементов без повторений П(h): 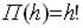    4. число перестановок из h элементов с повторениями ri, где i – номер символа из исходного множества, Пп(h): 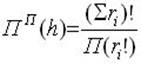  5. число размещений из h элементов по l без повторений Р(hl ): 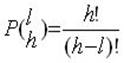6. число размещений из h элементов по l c повторениями Рп(hl ): 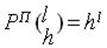Рассчитаем число получаемых подмножеств элементов для приведенного выше примера. Имеем: 1. число сочетаний из 3 элементов по 2 без повторений С(32 ): 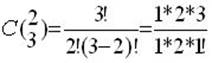2. число сочетаний из 3 элементов по 2 с повторениями Сп(32 ): 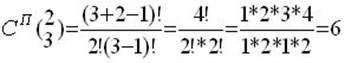  3. число перестановок из 3 элементов без повторений П(3): П(3) = 3! = 1*2*3 = 6 4. число перестановок из 3 элементов с повторениями Пп(3), причем ra = 2, rb = 1, rc = 1: 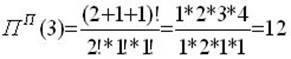5. число размещений из 3 элементов по 2 без повторений Р(32 ): 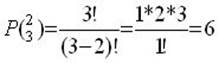6. число размещений из 3 элементов по 2 с повторениями Рп(32 ): Pп(32) = 32 = 9.