Примеры выполнения операций над множествами
Пример 1 (выполнение операций над конечными множествами)
Даны два конечных числовых множества А и В. Изобразить эти множества диаграммой Эйлера-Венна. Записать элементы множеств 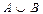 ,
, 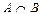 ,
, 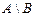 ,
, 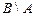 ,
, 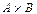 ,
,  .
.
а) 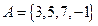 ,
, 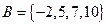 ; б)
; б) 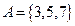 ,
, 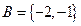 .
.
Решение
| а) Так как множества А и В имеют общие элементы, то для них диаграмма Эйлера-Венна имеет такой вид, как на рис. 10. Выполняем операции над множествами по их определениям: | 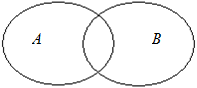 Рис. 10
Рис. 10
|
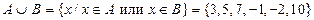 ;
; 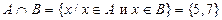 ;
;
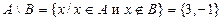 ;
; 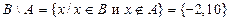 ;
;
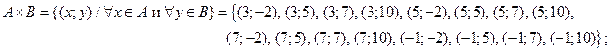
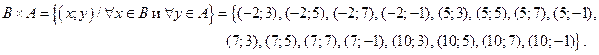
| б) Множества А и В не содержат одинаковых элементов, отображаем это диаграммой Эйлера-Венна так, как на рис. 11. | 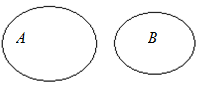 Рис. 11
Рис. 11
|
Записываем результаты выполнения операций над множествами A и B:
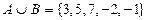 ; ; 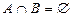 ; ; 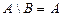 ; ; 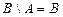 ; ;
| 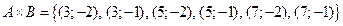 ; ; 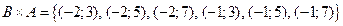 . .
|
Пример 2 (выполнение операций над бесконечными множествами)
Даны два бесконечных числовых множества 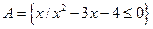 и
и 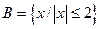 .
.
Записать промежутками множества A, B, 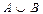 ,
, 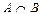 ,
, 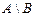 ,
, 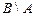 и изобразить эти множества геометрически на координатной прямой OX.
и изобразить эти множества геометрически на координатной прямой OX.
Множества 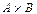 и
и  описать и построить на координатной плоскости XOY.
описать и построить на координатной плоскости XOY.
Решение
Находим множества А и В и изображаем их элементы на координатной оси:
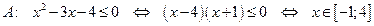

| 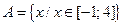 . .
|
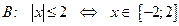
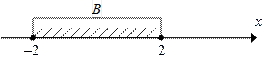
| 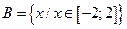 . .
|
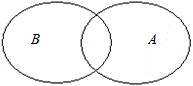
Для выполнения операций объединения, пересечения и разности множеств удобно множества А и В изобразить на одной координатной прямой (можно и кругами Эйлера):
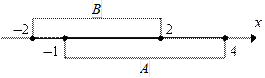
| 
|
Теперь выполняем операции над множествами, пользуясь определениями этих операций:
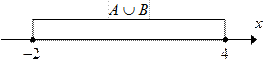
| 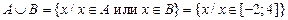 ; ;
|
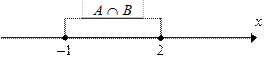
| 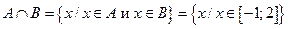 ; ;
|

| 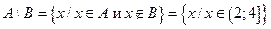 ; ;
|

| 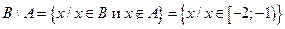 . .
|
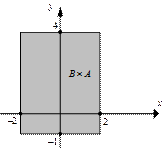
Множества 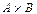 и и  описываем по определению декартова произведения множеств и строим на координатной плоскости XOY: описываем по определению декартова произведения множеств и строим на координатной плоскости XOY:
| |
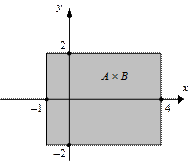
| 
|
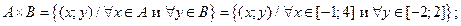
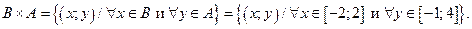
|
Пример 3 (определение элементов множества)
Записать элементы следующих множеств 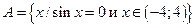 ,
, 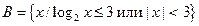 .
.
Решение
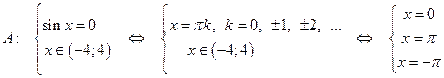
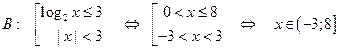 .
.
Ответ: 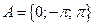 ,
, 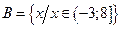 .
.
Пример 4 (множества точек на координатной плоскости)
Построить элементы множества 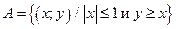 на коорд. плоскости XOY.
на коорд. плоскости XOY.
Решение
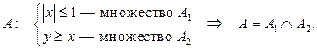
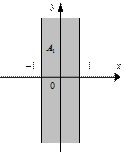
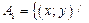
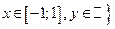 — это множество точек в полосе между прямыми x = –1 и x = 1, включающее в себя и точки на самих прямых;
— это множество точек в полосе между прямыми x = –1 и x = 1, включающее в себя и точки на самих прямых;
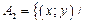
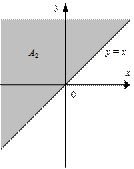
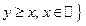 — это множество точек, расположенных выше прямой y = x; оно включает в себя и точки на самой прямой;
— это множество точек, расположенных выше прямой y = x; оно включает в себя и точки на самой прямой;
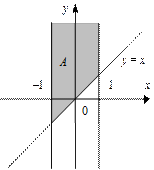
пересечением множеств A1 и A2 определяем искомое множество A.
Пример 5 (разбиение множества на подмножества)
Дано множество А натуральных чисел от 10 до 25 включительно. Разбить множество А на подмножества по принципу деления его элементов на числа 3 и 2.
Решение
Записываем множество А списком его элементов:
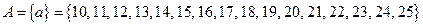 .
.
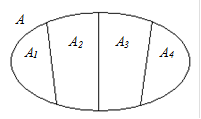
По признаку деления чисел а на числа 3 и 2 определяются следующие четыре непересекающиеся подмножества:
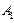 — множество чисел а, которые делятся на число 3, но не делятся на число 2;
— множество чисел а, которые делятся на число 3, но не делятся на число 2;
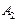 — множество чисел а, которые делятся на число 2, но не делятся на число 3;
— множество чисел а, которые делятся на число 2, но не делятся на число 3;
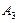 — множество чисел а, которые делятся и на число 3, и на число 2, т.е делятся на число 6;
— множество чисел а, которые делятся и на число 3, и на число 2, т.е делятся на число 6;
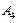 — множество чисел а, которые не делятся ни на число 3, ни на число 2.
— множество чисел а, которые не делятся ни на число 3, ни на число 2.
Очевидно, что множества 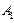 ,
, 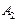 ,
, 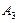 ,
, 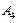 не пересекаются и их объединением получится данное множество А:
не пересекаются и их объединением получится данное множество А:
| 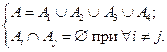
|
Теперь распределяем числа а по множествам 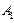 ,
, 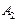 ,
, 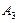 ,
, 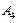 :
:
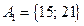 , ,
| 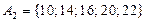 , ,
| 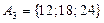 , ,
| 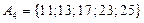 . .
|
Дата добавления: 2015-10-19; просмотров: 6225;
