Условный экстремум. Метод множителей Лагранжа
Если экстремум функции нескольких переменных вычисляется при наличии ограничений (связей) на независимые переменные[7], то говорят об условном эстремуме этой функции. Задача об условном экстремуме ставится так: найти экстремум функции  при наличии связей
при наличии связей 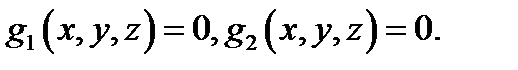 Дадим алгоритм решения этой задачи:
Дадим алгоритм решения этой задачи:
1. Составляем функцию Лагранжа 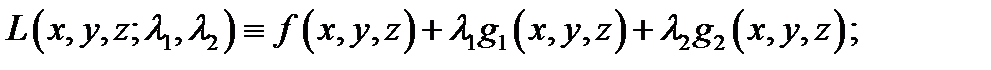
2. Находим критические точки 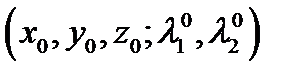 этой функции из системы уравнений
этой функции из системы уравнений
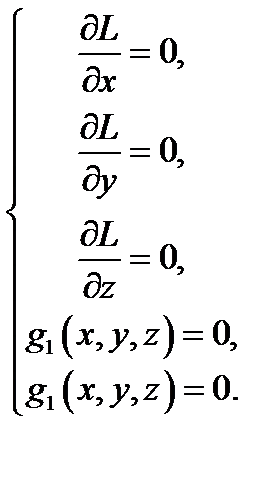
3. Вычисляем второй дифференциал функции Лагранжа (считая  постоянными):
постоянными):
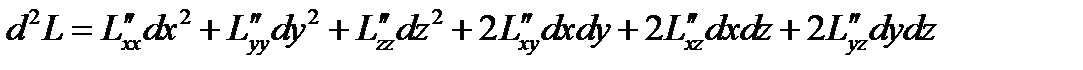
в фиксированной критической точке  , присоединяем к нему соотношения
, присоединяем к нему соотношения
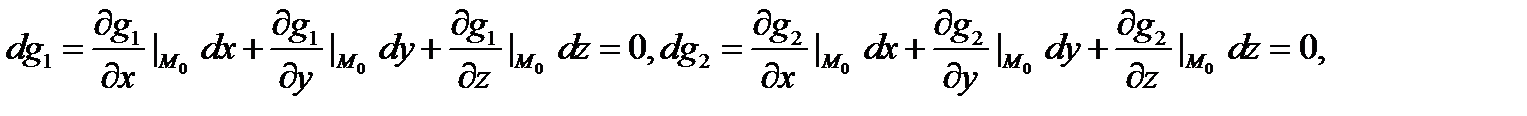
из которых выражаем зависимые дифференциалы как функции независимых, подставляем их
в 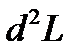 и устанавливаем знак полученного выражения
и устанавливаем знак полученного выражения 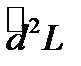 при условии что независимые дифференциалы изменяются в некоторой окрестности нуля. Если
при условии что независимые дифференциалы изменяются в некоторой окрестности нуля. Если 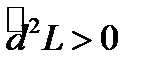 , то точка
, то точка 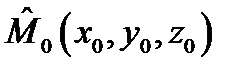 будет точкой условного минимума, если
будет точкой условного минимума, если 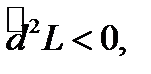 то точка
то точка 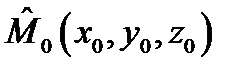 будет точкой условного максимума. И наконец, если
будет точкой условного максимума. И наконец, если 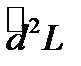 изменяет знак в любой окрестности нуля плоскости независимых дифференциалов, то в точке
изменяет знак в любой окрестности нуля плоскости независимых дифференциалов, то в точке 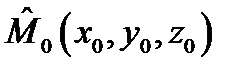 не будет условного экстремума.
не будет условного экстремума.
Покажем, как работает этот алгоритм, на конкретном примере. При этом ради простоты будем рассматривать функцию 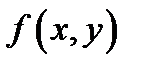 двух переменных и одну связь
двух переменных и одну связь 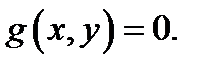 Пусть требуется найти экстремумы функции
Пусть требуется найти экстремумы функции 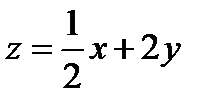 при условии
при условии 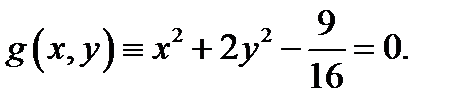
Запишем функцию Лагранжа
 .
.
Вычисляем частные производные и составляем систему уравнений:
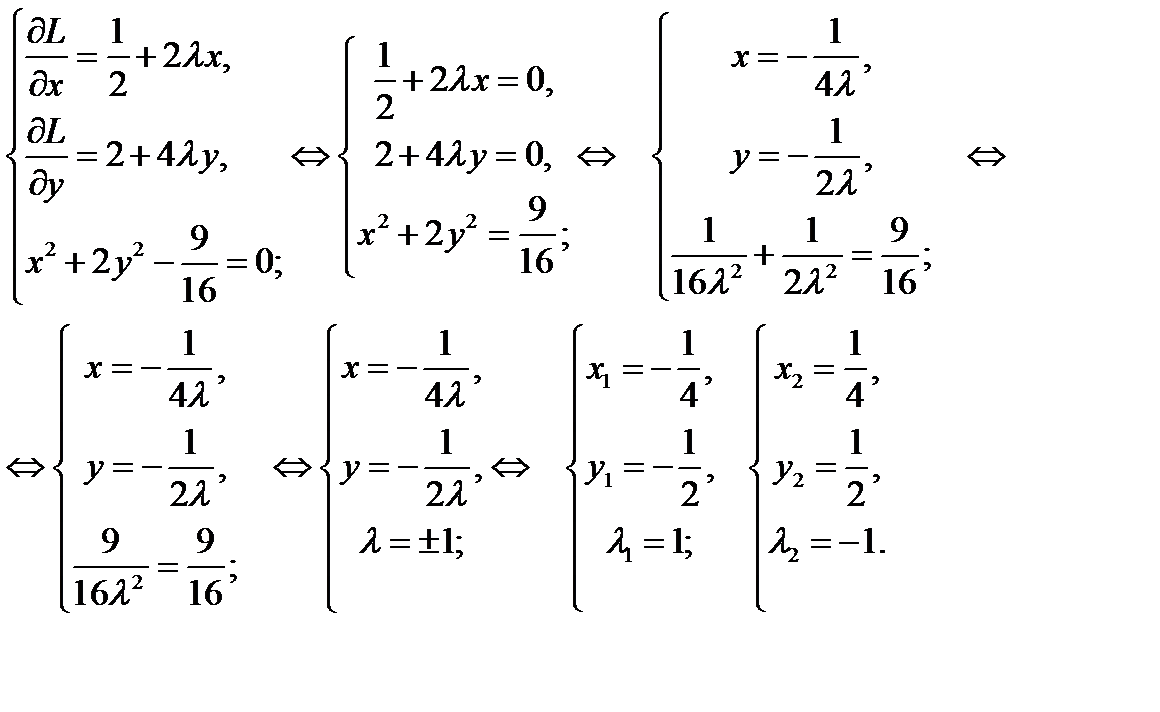
Получили две критические точки: 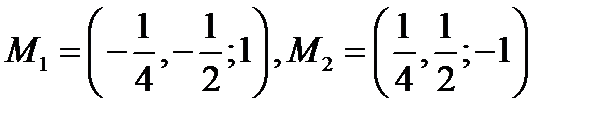 функции Лагранжа. Так как
функции Лагранжа. Так как
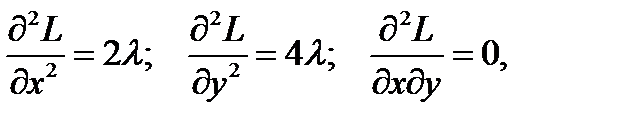
то  Здесь дифференциалы
Здесь дифференциалы 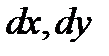 подчиняются условию
подчиняются условию 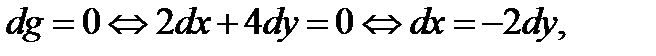 поэтому
поэтому 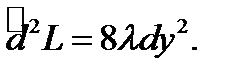 Отсюда видно, что в точке
Отсюда видно, что в точке 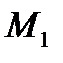 будет
будет 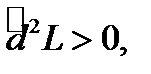 поэтому в точке
поэтому в точке 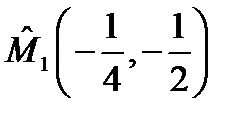 функция
функция 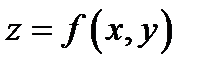 имеет условный минимум:
имеет условный минимум:
zmin= 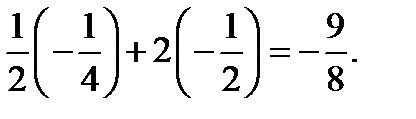
В точке  будет
будет  поэтому в точке
поэтому в точке 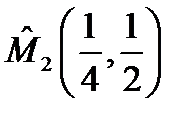 функция
функция 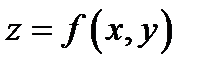 имеет условный максимум:
имеет условный максимум:
zmax= 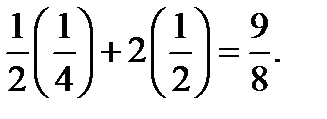
Дата добавления: 2017-03-29; просмотров: 1114;
