Свойства монотонных последовательностей
Давайте повторим это определение, используя в большей степени русский язык. Предел числовой последовательности существует и равен некоторому числу, если, начиная с некоторого номера, все члены
Определение 1. Числовая последовательность 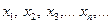 (1) называется монотонной, если для каждого натурального
(1) называется монотонной, если для каждого натурального 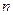 выполнено одно из четырех условий:
выполнено одно из четырех условий: 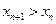 (2),
(2), 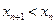 (3),
(3),  (4),
(4), 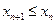 (5). В случае выполнения условия (2) последовательность (1) называется монотонно возрастающей. В случае выполнения условия (3) последовательность (1) называется монотонно убывающей. В случае выполнения условия (4) последовательность (1) называется монотонно неубывающей. В случае выполнения условия (5) последовательность (1) называется монотонно невозрастающей.
(5). В случае выполнения условия (2) последовательность (1) называется монотонно возрастающей. В случае выполнения условия (3) последовательность (1) называется монотонно убывающей. В случае выполнения условия (4) последовательность (1) называется монотонно неубывающей. В случае выполнения условия (5) последовательность (1) называется монотонно невозрастающей.
Теорема 1. Монотонная и ограниченная числовая последовательность имеет предел.
Доказательство. Достаточно доказать, что монотонно неубывающая последовательность (1) имеет предел. В самом деле, во-первых, возрастающая последовательность является частным случаем неубывающей последовательности. Во-вторых, если поменять знаки последовательности, то она из убывающей превратится в возрастающую.
Итак, пусть для последовательности (1) выполнено условие (4) и последовательность (1) ограничена. Но ведь ограниченное сверху множество имеет точную верхнюю грань, допустим – это число 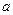 , для которого все
, для которого все 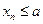 . Докажем, что в таком случае
. Докажем, что в таком случае 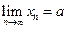 . Будем действовать в соответствии с определением предела числовой последовательности. Пусть задано число
. Будем действовать в соответствии с определением предела числовой последовательности. Пусть задано число 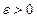 , тогда число
, тогда число 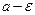 не является верхней гранью множества членов последовательности (1). Следовательно, существует номер
не является верхней гранью множества членов последовательности (1). Следовательно, существует номер 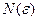 такое что
такое что 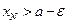 . Но тогда, в силу монотонности, при условии
. Но тогда, в силу монотонности, при условии 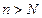 также
также 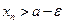 . С учетом соотношения
. С учетом соотношения 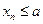 для этих членов числовой последовательности выполнено условие
для этих членов числовой последовательности выполнено условие 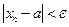 . А это и означает, что
. А это и означает, что 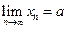 . Теорема доказана.
. Теорема доказана.
Бином Ньютона
Мы знаем, что 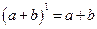 ,
,  и т. д. Формула бинома Ньютона обобщает эти правила на случай произвольной степени.
и т. д. Формула бинома Ньютона обобщает эти правила на случай произвольной степени.
Теорема 2. Справедлива формула бинома Ньютона 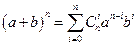 , (6) где
, (6) где 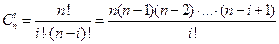 .
.
Доказательство. Теорема будет доказана методом математической индукции. Что такое метод математической индукции? Если утверждение надо доказать для всех натуральных значений параметра 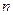 , то для этого достаточно доказать это утверждение для
, то для этого достаточно доказать это утверждение для 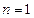 и затем доказать, что из справедливости утверждения для
и затем доказать, что из справедливости утверждения для 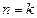 следует справедливость этого утверждения для
следует справедливость этого утверждения для 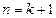 .
.
Проверим справедливость формулы (6) при 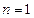 . Действительно,
. Действительно, 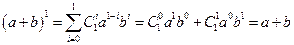 , т. к. (проверьте)
, т. к. (проверьте) 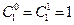 .
.
Пусть формула (6) справедлива при 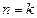 , т. е.
, т. е. 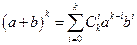 . Вычислим
. Вычислим 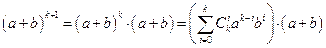 . Последнее произведение представляется в виде
. Последнее произведение представляется в виде 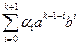 и при этом
и при этом 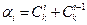 . С другой стороны, для проверки индуктивного предположения надо доказать, что
. С другой стороны, для проверки индуктивного предположения надо доказать, что 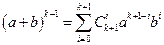 . Следовательно, для завершения доказательства теоремы Ньютона надо установить справедливость соотношения
. Следовательно, для завершения доказательства теоремы Ньютона надо установить справедливость соотношения 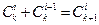 . Действительно,
. Действительно, 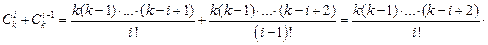
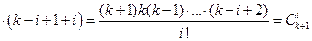 . Теорема доказана.
. Теорема доказана.
Кстати, величина 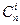 называется числом сочетаний из
называется числом сочетаний из 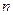 по
по 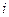 и показывает, сколькими способами можно выбрать
и показывает, сколькими способами можно выбрать 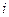 предметов из
предметов из 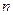 предметов.
предметов.
Число e
Рассмотрим числовую последовательность 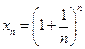 ,
, 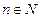 (7).
(7).
Теорема 3. Для членов числовой последовательности (7) справедливы соотношения: 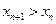 ,
, 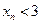 .
.
Доказательство. Для величины 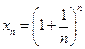 применим формулу бинома Ньютона. Следовательно,
применим формулу бинома Ньютона. Следовательно, 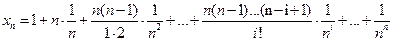 и отсюда
и отсюда 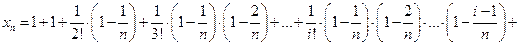
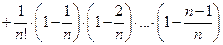 . Мы видим, что с ростом
. Мы видим, что с ростом 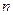 каждое слагаемое в последней записи
каждое слагаемое в последней записи 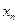 и число слагаемых увеличиваются. Следовательно,
и число слагаемых увеличиваются. Следовательно, 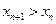 . Для доказательства второй части теоремы заметим, что
. Для доказательства второй части теоремы заметим, что 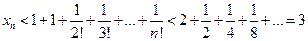 . Теорема доказана.
. Теорема доказана.
Итак, числовая последовательность (7) является монотонно возрастающей, ограниченной сверху последовательностью. Следовательно, она имеет предел. Этот предел является важной мировой константой, является трансцендентным числом и имеет специальное название.
Определение 2. Предел числовой последовательности (7) называется числом e.
Итак, по определению 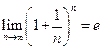 . (8)
. (8)
Дата добавления: 2019-07-26; просмотров: 1324;
