Основное определение и простейшие свойства
В курсе средней школы изучаются векторы-направленные отрезки. Этого требуют естественные науки, например, физика. Выясняется, что некоторые физические величины обладают не только скалярной величиной, но и направлением действия. Ввиду того, что приходится описывать взаимодействие таких величин, вводятся операции над ними. Одна из них – сложение – может рассматриваться как БАО. Вторая же отличается тем, что в ней участвуют элементы разных по природе множеств. Это операция умножения направленного отрезка на вещественное число. Будем называть такую операцию внешним умножением. Из свойств операции сложения легко вывести тот факт, что направленные отрезки данной прямой, данной плоскости и пространства наделяются групповой структурой. Кроме того, операция внешнего умножения имеет вполне естественные свойства, и связь между операциями легко доказывается геометрически. Основной задачей данной главы будет построение новой алгебраической структуры, которая появляется за счет аксиоматизации свойств направленных отрезков, заданных групповых структур. Эта новая структура является основной средой линейной алгебры. Как правило, все построения в линейной алгебре выполняются в некотором линейном пространстве.
Определение 5.1. Пусть задано произвольное множество 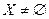 и поле Р. Тогда пара
и поле Р. Тогда пара 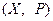 называется абстрактным линейным пространством Х над полем Р (в дальнейшем – просто пространством Х или ЛП Х), если
называется абстрактным линейным пространством Х над полем Р (в дальнейшем – просто пространством Х или ЛП Х), если
1.  На Х задана БАО сложения «+», относительно которой Х является абелевой группой;
На Х задана БАО сложения «+», относительно которой Х является абелевой группой;
2.  Задано отображение
Задано отображение 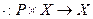 , называемое внешним умножением элементов поля на элементы Х, удовлетворяющее следующим аксиомам:
, называемое внешним умножением элементов поля на элементы Х, удовлетворяющее следующим аксиомам:
1. 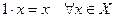 ;
;
2. 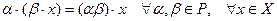 .
.
3.  1.
1. 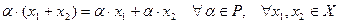 ;
;
2. 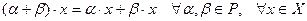 .
.
Элементы множества Х называем векторами, а элементы поля Р– скалярами. Если поле Р является рациональным, вещественным или комплексным, то линейное пространство в свою очередь называется соответственно рациональным, вещественным или комплексным. В дальнейшем точку, изображающую операцию внешнего умножения, будем, как правило, опускать.
Как видно из определения 5.1, аксиомы линейного пространства повторяют свойства направленных отрезков прямой, плоскости и пространства. Поэтому эти пространства являются естественными примерами такой структуры.
Пример 5.1. Каждое поле Р над самим собой представляет линейное пространство. В данном случае векторы и скаляры формально одинаковы.
Пример 5.2. Пусть 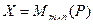 , тогда
, тогда 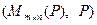 – линейное пространство. В частности
– линейное пространство. В частности 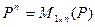 или
или 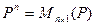 являются пространствами строк или столбцов.
являются пространствами строк или столбцов.
Пример 5.3. Пусть 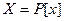 , тогда
, тогда 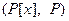 – линейное пространство.
– линейное пространство.
Пример 5.4. Пусть 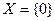 , а Р – любое числовое поле, тогда
, а Р – любое числовое поле, тогда 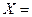 0 – нулевое пространство.
0 – нулевое пространство.
Пример 5.5. Пусть 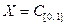 – множество вещественных непрерывных функций, заданных на отрезке [0, 1]. Тогда получаем вещественное линейное пространство.
– множество вещественных непрерывных функций, заданных на отрезке [0, 1]. Тогда получаем вещественное линейное пространство.
Отметим несколько простейших, но важных, следствий из аксиом. Нулевой элемент поля графически будет совпадать с изображением нулевого вектора, но из контекста будет ясно, где вектор.
1. 
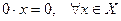 ;
;
2. 
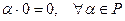 ;
;
3. 
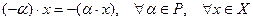 ; в частности,
; в частности,
4. 
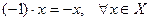 ;
;
5. 
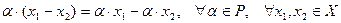 ;
;
6. 
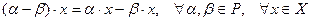 ;
;
7. 
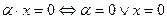 ;
;
8.  Если
Если  , то
, то 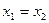 ;
;
9.  Если
Если 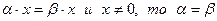 .
.
В последних двух позициях представлены законы сокращения на общий ненулевой скаляр и общий ненулевой вектор.
Подпространства и линейные оболочки
Как и в случаях других алгебраических структур, определим подструктуру.
Определение 5.2. Пусть 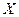 линейное пространство над полем Р и
линейное пространство над полем Р и 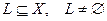 . Тогда
. Тогда 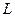 называется подпространством пространства Х, если само является линейным пространством относительно сужения операций, определенных для Х.
называется подпространством пространства Х, если само является линейным пространством относительно сужения операций, определенных для Х.
Нулевое подпространство и само Х называются тривиальными подпространствами.
Пример 5.6. Направленные отрезки, лежащие в некоторой плоскости, образуют подпространство трехмерного пространства.
Пример 5.7. Диагональные матрицы образуют подпространство в пространстве квадратных матриц данного порядка над полем Р.
Ясно, что для того, чтобы доказать, что 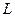 подпространство в Х, надо просмотреть выполнимость аксиом ЛП. Но можно воспользоваться специальной теоремой.
подпространство в Х, надо просмотреть выполнимость аксиом ЛП. Но можно воспользоваться специальной теоремой.
Теорема 5.1 (критерий подпространства).
Непустое подмножество 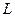 линейного пространства Х над полем Р является его подпространством тогда и только тогда, когда
линейного пространства Х над полем Р является его подпространством тогда и только тогда, когда 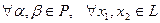 выполнено
выполнено  .
.
Необходимость очевидна, а достаточность легко доказывается, ибо 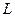 должна быть подгруппой аддитивной группы пространства.
должна быть подгруппой аддитивной группы пространства.
Пример 5.8. Пусть 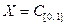 , а
, а 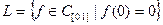 . Покажем, что
. Покажем, что 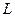 – подпространство в Х.
– подпространство в Х.

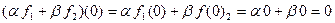 , следовательно,
, следовательно, 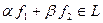 .
.
Определение 5.3. Пусть Х линейное пространство над полем Р. Системой векторов в Х называется конечный упорядоченный набор векторов из Х. Любой поднабор данной системы будет называться подсистемой этой системы.
Определение 5.4. Пусть задана система векторов пространства Х над полем Р 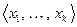 и набор элементов поля
и набор элементов поля 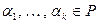 , тогда вектор
, тогда вектор 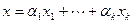 называется линейной комбинацией (ЛК) векторов системы
называется линейной комбинацией (ЛК) векторов системы 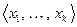 . Элементы поля
. Элементы поля 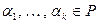 называются коэффициентами линейной комбинации. А вектор х называют линейно выражающимся через систему
называются коэффициентами линейной комбинации. А вектор х называют линейно выражающимся через систему 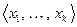 с коэффициентами
с коэффициентами 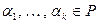 .
.
Определение 5.5. Множество всех линейных комбинаций данной системы векторов называется линейной оболочкой системы.
Линейную оболочку системы 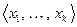 обозначим
обозначим 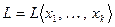 .
.
Лемма 5.1. Линейная оболочка всякой системы векторов линейного пространства является его подпространством.
Лемма 5.2 (о транзитивности линейных комбинаций).
Если система 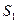 линейно выражается через систему
линейно выражается через систему 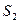 , а система
, а система 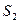 линейно выражается через систему
линейно выражается через систему 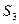 , то система
, то система 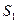 линейно выражается через систему
линейно выражается через систему 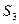 .
.
Линейная зависимость
В этом разделе рассматривается краеугольное понятие всей линейной алгебры. Вопрос, который возникает после определения линейной оболочки, звучит так: какой может быть система, порождающая данную линейную оболочку? Проведем мысленный эксперимент. Пусть задана ненулевая система векторов 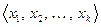 . Предположим, что первый вектор
. Предположим, что первый вектор  линейно выражается через остальные векторы. Значит, в соответствующей линейной оболочке можно первый вектор заменить его представлением через остальные, и, таким образом,
линейно выражается через остальные векторы. Значит, в соответствующей линейной оболочке можно первый вектор заменить его представлением через остальные, и, таким образом, 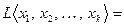
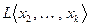 . Далее, может быть, что некоторый другой вектор, например,
. Далее, может быть, что некоторый другой вектор, например,  линейно выражается через систему
линейно выражается через систему 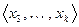 , и тогда
, и тогда 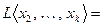
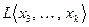 и так далее. Поступая подобным образом, т.е. удаляя «лишние» векторы приходим к подсистеме, из которой уже нельзя убрать ни одного вектора без разрушения линейной оболочки. Такая подсистема заведомо существует. В крайнем случае, в ней останется один вектор. Памятуя о том, что исходная система была ненулевой, утверждаем, что и подсистема будет таковой. Таким образом, исходную линейную оболочку представляется возможным описать экономным способом, строя ее на «минимальной» системе. Этот эксперимент приводит к следующему определению.
и так далее. Поступая подобным образом, т.е. удаляя «лишние» векторы приходим к подсистеме, из которой уже нельзя убрать ни одного вектора без разрушения линейной оболочки. Такая подсистема заведомо существует. В крайнем случае, в ней останется один вектор. Памятуя о том, что исходная система была ненулевой, утверждаем, что и подсистема будет таковой. Таким образом, исходную линейную оболочку представляется возможным описать экономным способом, строя ее на «минимальной» системе. Этот эксперимент приводит к следующему определению.
Определение 5.6. Система векторов 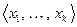 линейного пространства называется линейно независимой (ЛНЗ), если при
линейного пространства называется линейно независимой (ЛНЗ), если при
1. 
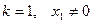 ;
;
2. 
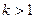 ни один вектор системы линейно не выражается через остальные.
ни один вектор системы линейно не выражается через остальные.
Определение 5.7. Система, не являющаяся линейно независимой называется линейно зависимой (ЛЗ), т.е. при
1. 
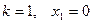 ;
;
2. 
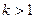 существует вектор системы линейно выражающийся через остальные.
существует вектор системы линейно выражающийся через остальные.
Проведенное рассуждение позволяет сформулировать небольшой результат.
Лемма 5.3. Каждая ненулевая система содержит линейно независимую подсистему, порождающую ту же линейную оболочку.
Вопрос выявления свойства линейной независимости у системы по определению может оказаться непростым, ибо не всегда явно видны линейные представления векторов. Поэтому обратимся к результату, решающему эту задачу проще.
Теорема 5.2 (критерий линейной независимости).
Система векторов линейного пространства линейно независима тогда и только тогда, когда из равенства нулю линейной комбинации векторов системы следует равенство нулю всех коэффициентов линейной комбинации.
Доказательство. Необходимость. Пусть задана система 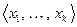 и сначала
и сначала 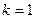 .Тогда имеем
.Тогда имеем 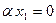 . Так как
. Так как 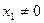 ввиду линейной независимости системы, то по
ввиду линейной независимости системы, то по
свойству 7  следствий из аксиом получаем, что
следствий из аксиом получаем, что 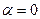 . Пусть теперь
. Пусть теперь 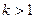 . Предположим противное. Пусть существует линейная комбинация векторов системы, равная нулю, с ненулевыми коэффициентами:
. Предположим противное. Пусть существует линейная комбинация векторов системы, равная нулю, с ненулевыми коэффициентами:
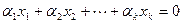 .
.
Пусть, например, 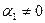 . Тогда получим по следствиям из аксиом
. Тогда получим по следствиям из аксиом
 .
.
Значит, в системе есть вектор, линейно выражающийся через остальные векторы, т.е. она не является линейно независимой. Противоречие доказывает результат.
Достаточность. Снова пусть сначала 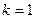 . Тогда
. Тогда 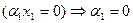 . Тогда
. Тогда 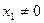 , что равносильно линейной независимости системы. Теперь пусть
, что равносильно линейной независимости системы. Теперь пусть 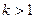 . Опять рассуждаем от противного. Пусть в системе имеется вектор линейно выражающийся через остальные, например,
. Опять рассуждаем от противного. Пусть в системе имеется вектор линейно выражающийся через остальные, например,  . Именно
. Именно
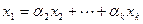 .
.
Тогда, выполняя преобразования равенства, используя следствия из аксиом, получим:
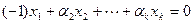 .
.
Значит, получаем противоречие, ибо не все коэффициенты линейной комбинации заведомо равны нулю.
Теорема полностью доказана. Из этой теоремы можно получить легко критерий линейной зависимости системы.
Теорема 5.3 (первый критерий линейной зависимости).
Система векторов линейного пространства линейно зависима тогда и только тогда, когда существует линейная комбинация векторов системы, равная нулю, с ненулевым набором коэффициентов.
Эту теорему полезно доказать не опираясь на предыдущую.
Замечание. Важно осознавать, что свойство линейной зависимости или независимости является системным, т.е. относится к системам векторов, а не к отдельным элементам систем.
Пример 5.9. Проверить, является ли система 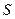 векторов из
векторов из 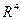 линейно зависимой.
линейно зависимой.

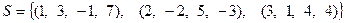 .
.
Составим линейную комбинацию системы и приравняем ее нулю:
 .
.
Теперь, используя понятие равенства матриц и умножая каждый вектор на свой коэффициент, получаем линейную систему:
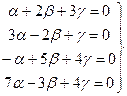 .
.
Решаем систему методом Гаусса.
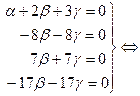
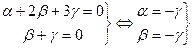 .
.
Очевидно, что система имеет ненулевое решение. Таким образом, система векторов оказывается линейно зависимой по первому критерию линейной зависимости.
Рассмотрим простейшие свойства ЛЗ и ЛНЗ систем.
1.  Система, содержащая нулевой вектор, линейно зависима.
Система, содержащая нулевой вектор, линейно зависима.
2.  Система, содержащая равные векторы, линейно зависима.
Система, содержащая равные векторы, линейно зависима.
3.  Система, содержащая пропорциональные векторы, линейно зависима.
Система, содержащая пропорциональные векторы, линейно зависима.
4.  Система, содержащая линейно зависимую подсистему, сама линейно зависима.
Система, содержащая линейно зависимую подсистему, сама линейно зависима.
5.  Любая подсистема линейно независимой системы сама линейно независима.
Любая подсистема линейно независимой системы сама линейно независима.
Иногда удобно применять критерий ЛЗ, использующий свойство упорядоченности системы векторов.
Теорема 5.4 (второй критерий линейной зависимости).
Система векторов 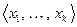 линейно зависима тогда и только тогда, когда либо
линейно зависима тогда и только тогда, когда либо 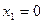 , либо существует вектор
, либо существует вектор 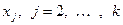 , линейно выражающийся через предыдущие векторы системы.
, линейно выражающийся через предыдущие векторы системы.
Доказательство. Достаточность очевидна. Докажем необходимость. Из того, что система линейно зависима, следует по первому критерию существование линейной комбинации векторов системы, равной нулю, с ненулевым набором коэффициентов:
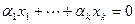 .
.
Пусть 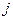 будет наибольшим номером с условием
будет наибольшим номером с условием 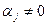 ,
, 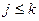 , т.е. имеем равенство
, т.е. имеем равенство
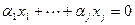 .
.
Тогда, если 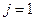 , то имеем первую часть утверждения, а иначе – вторую, т.е.
, то имеем первую часть утверждения, а иначе – вторую, т.е.
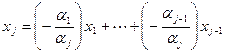 .
.
Теорема доказана.
Эквивалентные системы векторов
Определение 5.8. Две системы векторов называются эквивалентными, если каждая из них линейно выражается через другую систему.
Лемма 5.4 (критерий эквивалентности).
Две системы векторов линейного пространства эквивалентны тогда и только тогда, когда совпадают их линейные оболочки.
Лемма 5.5. Бинарное отношение эквивалентности систем векторов является отношением эквивалентности, т.е. рефлексивно, симметрично и транзитивно.
Из последней леммы следует, что все системы векторов данного пространства можно разбить на попарно непересекающиеся классы эквивалентности. Каждому такому классу будет отвечать некоторая линейная оболочка.
Теорема 5.5 (сравнения).
Пусть заданы две системы векторов: 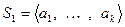 и
и 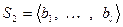 , причем первая – линейно независимая. Тогда, если каждый вектор
, причем первая – линейно независимая. Тогда, если каждый вектор 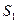 линейно выражается через
линейно выражается через
векторы 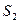 , то
, то 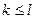 .
.
Доказательство. Построим новую систему 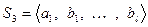 . Эта система линейно зависима, ибо первый вектор
. Эта система линейно зависима, ибо первый вектор 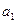 линейно выражается через остальные. Применим к этой системе теорему 5.4. Так как
линейно выражается через остальные. Применим к этой системе теорему 5.4. Так как 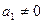 , как вектор из ЛНЗ системы, то найдется вектор
, как вектор из ЛНЗ системы, то найдется вектор 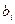 ,
, 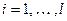 , такой, что линейно выражается через предыдущие. Поэтому в линейных представлениях векторов системы
, такой, что линейно выражается через предыдущие. Поэтому в линейных представлениях векторов системы 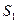 он может быть заменен соответствующими линейными комбинациями. Если вектор
он может быть заменен соответствующими линейными комбинациями. Если вектор 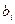 удалить из системы
удалить из системы 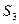 , то получим систему
, то получим систему 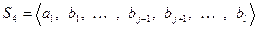 , через которую выражается система
, через которую выражается система 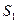 . Добавим слева в
. Добавим слева в 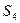 вектор
вектор 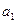 и получим систему
и получим систему 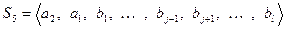 , которая, очевидно, является ЛЗ. И согласно второму критерию ЛЗ в ней должен быть вектор, выражающийся через предыдущие. Но этим не может быть вектор
, которая, очевидно, является ЛЗ. И согласно второму критерию ЛЗ в ней должен быть вектор, выражающийся через предыдущие. Но этим не может быть вектор 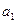 , так как принадлежит ЛНЗ системе, и
, так как принадлежит ЛНЗ системе, и 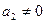 по той же причине. Поэтому найдется вектор
по той же причине. Поэтому найдется вектор 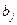 , который выражается через предыдущие. Если его удалить из системы
, который выражается через предыдущие. Если его удалить из системы 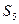 , то получим систему
, то получим систему 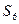 , через которую выражается
, через которую выражается 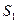 . Присоединим к
. Присоединим к 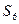 вектор
вектор 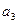 слева и т.д. В этой процедуре важно то, что после удаления вектора системы
слева и т.д. В этой процедуре важно то, что после удаления вектора системы 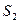 получается система, через которую линейно выражается система
получается система, через которую линейно выражается система 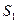 . При этом векторы
. При этом векторы 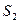 не могут исчерпаться ранее того, как будут присоединены все векторы из
не могут исчерпаться ранее того, как будут присоединены все векторы из 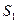 . Что и означает
. Что и означает 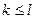 .
.
Следствие 1. Эквивалентные линейно независимые системы содержат одинаковое количество векторов.
Следствие 2. Каждая система из более 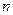 векторов взятая из линейной оболочки, построенной на
векторов взятая из линейной оболочки, построенной на 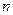 векторах, линейно зависима.
векторах, линейно зависима.
Определение 5.9. Базой ненулевой системы векторов называется эквивалентная ей подсистема.
Замечание. Нулевая система базы не имеет.
Рассмотрим некоторые свойства базы.
1.  База ЛНЗ системы совпадает с самой системой.
База ЛНЗ системы совпадает с самой системой.
2.  Подсистема ненулевой системы будет ее базой тогда и только тогда, когда она максимально ЛНЗ.
Подсистема ненулевой системы будет ее базой тогда и только тогда, когда она максимально ЛНЗ.
Замечание. Максимально ЛНЗ подсистема та, к которой нельзя присоединить ни одного вектора системы, сохраняя свойство ЛНЗ.
3.  База системы не изменится, если к системе добавить вектор, являющийся линейной комбинацией векторов системы.
База системы не изменится, если к системе добавить вектор, являющийся линейной комбинацией векторов системы.
4.  Каждый вектор системы линейно выражается через векторы базы единственным образом.
Каждый вектор системы линейно выражается через векторы базы единственным образом.
Доказательство последнего свойства можно вывести из того факта, что если вектор выражается через ЛНЗ систему, то это его представление единственно. Действительно, пусть вектор 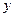 линейно выражается через ЛНЗ систему
линейно выражается через ЛНЗ систему 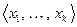 двумя способами.
двумя способами.
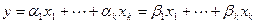 .
.
Тогда 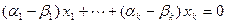 ,
,
И по критерию ЛНЗ получаем, что 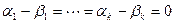 , т.е.
, т.е. 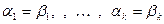 .
.
Однозначное описание вектора линейной оболочки через базу порождающей системы можно осуществить, отображая сам вектор в строку коэффициентов, которую удобно назвать координатной строкой вектора в данной базе: если 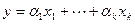 , то
, то
 .
.
Такое отображение, очевидно, обладает линейными свойствами, т.е., линейные операции над векторами отвечают такие же операции над координатными строками.
Учитывая следствие 1 предыдущей теоремы, можно утверждать, что две базы одной и той же системы эквивалентны. Отсюда получаем новое определение.
Определение 5.10. Рангом ненулевой системы векторов называется число векторов какой-либо его базы. Ранг нулевой системы считается равным нулю.
Рассмотрим теперь некоторые свойства ранга системы.
1.  Ранг ЛНЗ системы равен числу векторов системы.
Ранг ЛНЗ системы равен числу векторов системы.
2.  Ранг ЛЗ системы меньше числа векторов системы.
Ранг ЛЗ системы меньше числа векторов системы.
3.  Ранги эквивалентных систем равны.
Ранги эквивалентных систем равны.
4.  Ранг подсистемы не превосходит ранга системы.
Ранг подсистемы не превосходит ранга системы.
5.  Если ранг подсистемы равен рангу системы, то у них есть общая база.
Если ранг подсистемы равен рангу системы, то у них есть общая база.
6.  Если система
Если система 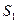 линейно выражается через систему
линейно выражается через систему 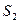 , то ранг
, то ранг 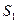 не превосходит ранга
не превосходит ранга 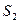 .
.
7.  Ранг системы не изменится, если к ней присоединить или удалить из нее вектор, являющийся линейной комбинацией остальных.
Ранг системы не изменится, если к ней присоединить или удалить из нее вектор, являющийся линейной комбинацией остальных.
Рассмотрим теперь, т.н., элементарные преобразования системы векторов.
Определение 5.11. Элементарными преобразованиями (ЭП) системы векторов называют следующие:
1.  Перемена местами (транспозиция) двух векторов системы;
Перемена местами (транспозиция) двух векторов системы;
2.  Умножение любого вектора системы на элемент поля
Умножение любого вектора системы на элемент поля 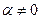 ;
;
3.  Прибавление к любому вектору любого другого вектора системы, умноженного на произвольный элемент поля.
Прибавление к любому вектору любого другого вектора системы, умноженного на произвольный элемент поля.
Лемма 5.6. Элементарные преобразования системы векторов являются эквивалентными, т.е., приводят к системе эквивалентной данной.
Посмотрим теперь, как можно вычислять базу и ранг системы, пользуясь элементарными преобразованиями. Это удобно сделать на примере работы с матрицами-строками, ибо, как было сказано, векторы легко описывать в координатной форме.
Пример 5.10. Пусть задана система векторов
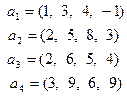 .
.
Найдем какую-либо ее базу и определим ранг. Для этого приведем ее элементарными, а значит эквивалентными, преобразованиями к треугольному (трапецеидальному) виду. Получим
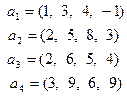
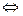
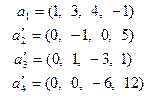
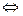
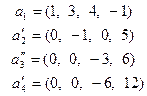
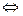

Ясно, что последняя система эквивалентна исходной. Нулевой вектор не может входить в базу и поэтому его естественно удалить. После чего остается три вектора, образующие ЛНЗ систему, ибо ни один из них не может быть выражен через нижестоящие, а первый вектор не равен нулю (см. теорему 5.4). Поэтому ранг последней системы, а значит и первой, равен трем. Так как векторы не переставлялись местами и сохранили свои номера, то первые три вектора исходной системы образуют одну из ее баз.
Базис линейного пространства
Все линейные пространства над данным полем можно распределить по двум классам. Эти классы возникают ввиду следующего определения.
Определение 5.12. Линейное пространство называется конечномерным, если существует такая константа М, что любая линейно независимая система содержит не более М векторов. В противном случае пространство называется бесконечномерным.
Нулевое пространство будем считать конечномерным.
Пример 5.11. Бесконечномерным пространством является (  ). Действительно,
). Действительно,
рассмотрим систему векторов 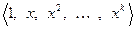 . Как легко видеть, она ЛНЗ. Ибо из равенства
. Как легко видеть, она ЛНЗ. Ибо из равенства  следует, что
следует, что  . Так как
. Так как  произвольно, то не существует ограничения М.
произвольно, то не существует ограничения М.
Пример 5.12. Бесконечномерным будет и пространство ( 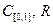 ).
).
В дальнейшем будем рассматривать лишь конечномерные пространства. Пусть Х такое пространство. Рассмотрим в нем ЛНЗ систему, содержащую максимальное число векторов: 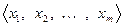 . Дополняя эту систему произвольным вектором
. Дополняя эту систему произвольным вектором 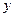 , получаем уже ЛЗ систему:
, получаем уже ЛЗ систему: 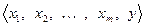 . Согласно теореме 5.4 вектор
. Согласно теореме 5.4 вектор 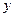 линейно выражается через исходную систему. Именно:
линейно выражается через исходную систему. Именно:
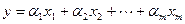 .
.
Отсюда получаем определение родственное понятию «база системы».
Определение 5.13. Линейно независимая система векторов конечномерного пространства, через которую линейно выражается каждый вектор этого пространства, называется базисом пространства.
Лемма 5.7. Каждое конечномерное пространство является линейной оболочкой своего базиса.
Лемма 5.8. Каждое подпространство конечномерного пространства само является конечномерным.
Лемма 5.9. Каждое подпространство конечномерного пространства является линейной оболочкой некоторой системы.
В силу того, что два базиса конечномерного пространства, очевидно, эквивалентны, получаем числовую характеристику пространства, родственную понятию «ранг системы».
Определение 5.14. Размерностью ненулевого пространства называется число векторов любого его базиса. Размерность нулевого пространства считаем равной нулю.
Обозначение для размерности пространства Х: 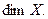
Опишем некоторые свойства базиса в виде несложных лемм.
Лемма 5.10. Любая линейно независимая система 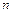 -мерного пространства, содержащая
-мерного пространства, содержащая 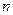 векторов, является базисом этого пространства.
векторов, является базисом этого пространства.
Лемма 5.11. Любая система 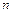 -мерного пространства, содержащая более
-мерного пространства, содержащая более 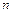 векторов линейно зависима.
векторов линейно зависима.
Лемма 5.12. Представление любого вектора в виде разложения по базису единственно.
Лемма 5.13 (критерий базиса). Система векторов является базисом пространства тогда и только тогда, когда она максимально линейно независима.
Лемма 5.14. Каждую линейно независимую систему векторов линейного пространства можно дополнить до базиса этого пространства.
Пример 5.13. Рассмотрим пространство 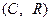 , т.е., множество комплексных чисел над полем
, т.е., множество комплексных чисел над полем 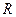 . Очевидно, что базисом такого пространства может служить система
. Очевидно, что базисом такого пространства может служить система 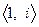 . Она линейно независима над полем
. Она линейно независима над полем 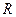 , Каждый вектор
, Каждый вектор 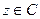 однозначно линейно выражается через такую систему:
однозначно линейно выражается через такую систему: 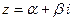 . Размерность этого пространства равна двум, т.е.
. Размерность этого пространства равна двум, т.е. 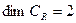 .
.
Пример 5.14. Рассмотрим пространство 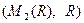 . Любую матрицу этого пространства можно однозначно представить через линейно независимую систему матриц
. Любую матрицу этого пространства можно однозначно представить через линейно независимую систему матриц
 .
.
Действительно, 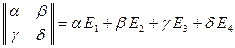 . Поэтому
. Поэтому 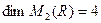 .
.
Вновь, как и в случае с базами, сопоставим каждому вектору линейного пространства матрицу-строку или матрицу-столбец, составленные из коэффициентов разложения этого вектора по данному базису. Если 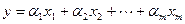 , то
, то 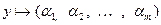 назовем соответствующий набор координатной строкой (столбцом) вектора в данном базисе. Ввиду леммы 5.12 этот набор определяется базисом однозначно. Легко видеть, что данное отображение обладает линейными свойствами, т.е., сумме векторов отвечает сумма их координатных строк (столбцов), а произведению элемента поля на вектор отвечает произведение этого же элемента на координатную строку (столбец). Примем теперь обозначение для координатного столбца вектора
назовем соответствующий набор координатной строкой (столбцом) вектора в данном базисе. Ввиду леммы 5.12 этот набор определяется базисом однозначно. Легко видеть, что данное отображение обладает линейными свойствами, т.е., сумме векторов отвечает сумма их координатных строк (столбцов), а произведению элемента поля на вектор отвечает произведение этого же элемента на координатную строку (столбец). Примем теперь обозначение для координатного столбца вектора 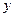 в базисе
в базисе 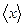 как
как 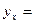
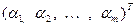 . И зададимся вопросом, как изменяются координаты вектора, если перейти к другому базису. Для этого зададим два базиса
. И зададимся вопросом, как изменяются координаты вектора, если перейти к другому базису. Для этого зададим два базиса 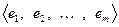 и
и 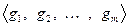 , а также координатные столбцы вектора х в указанных базисах
, а также координатные столбцы вектора х в указанных базисах 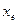 и
и 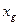 . Нужно указать связь между
. Нужно указать связь между 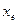 и
и 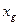 . Для этого выразим векторы второго базиса через векторы первого линейно. Получим
. Для этого выразим векторы второго базиса через векторы первого линейно. Получим
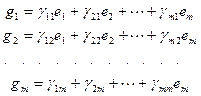 , или
, или 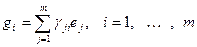 .
.
Составим матрицу Г из коэффициентов разложения векторов базиса 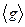 по базису
по базису 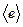 и транспонируем ее, так что нумерация строк и столбцов станет обычной. Тогда матрица Г примет вид:
и транспонируем ее, так что нумерация строк и столбцов станет обычной. Тогда матрица Г примет вид:
 .
.
Легко видеть, что 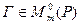 , т.е. матрица является невырожденной. Действительно, если бы она была вырожденной, то были бы линейно зависимы ее столбцы (какой-то столбец являлся бы линейной комбинацией остальных, что следует из равенства определителя нулю). Но тогда была бы линейно зависима система
, т.е. матрица является невырожденной. Действительно, если бы она была вырожденной, то были бы линейно зависимы ее столбцы (какой-то столбец являлся бы линейной комбинацией остальных, что следует из равенства определителя нулю). Но тогда была бы линейно зависима система 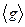 , что невозможно. Эту матрицу назовем матрицей перехода от базиса
, что невозможно. Эту матрицу назовем матрицей перехода от базиса 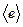 к базису
к базису 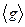 . Далее, пусть
. Далее, пусть  . Тогда
. Тогда
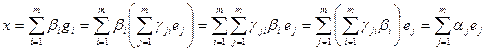 .
.
В силу единственности представления вектора через базис получаем, что
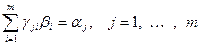 .
.
В матричной форме это выглядит так:  . Или
. Или 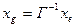 . Эти формулы и представляют собой закон преобразования координат при переходе от одного базиса к другому. Рассмотрим маленький пример.
. Эти формулы и представляют собой закон преобразования координат при переходе от одного базиса к другому. Рассмотрим маленький пример.
Пример 5.15. Пусть задан вектор 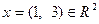 и базисы
и базисы 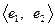 ,
, 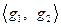 . При этом
. При этом 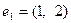 ,
, 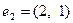 , а
, а 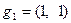 ,
, 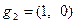 . Тогда
. Тогда 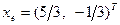 . Матрица
. Матрица
перехода от 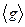 к
к 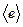 будет
будет 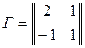 и, наконец,
и, наконец, 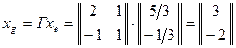 .
.
Последнее можно проверить непосредственно.
Суммы и пересечения подпространств
В этом разделе будут определены и изучены несколько специальных конструкций в линейном пространстве.
Определение 5.15. Пусть 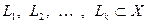 – подпространства в пространстве Х. Тогда множество
– подпространства в пространстве Х. Тогда множество  называется суммой подпространств
называется суммой подпространств 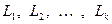 .
.
Для случая двух слагаемых можно выделить следующие свойства:
1. 
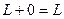 ;
;
2. 
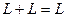 ;
;
3. 
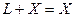 .
.
Лемма 5.15. Сумма подпространств пространства Х есть подпространство в Х.
Определение 5.16. Пересечением подпространств 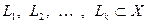 пространства Х называется теоретико-множественное пересечение соответствующих множеств векторов, т.е.,
пространства Х называется теоретико-множественное пересечение соответствующих множеств векторов, т.е., 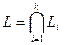 .
.
Простейшие свойства пересечения:
1. 
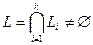 ;
;
2. 
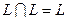 ;
;
3. 
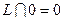 ;
;
4. 
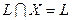 .
.
Лемма 5.16. Пересечение подпространств пространства Х есть подпространство в Х.
В силу того, что названные множества являются в свою очередь подпространствами, то в конечномерном случае они имеют размерность. Соотношение между размерностями суммы и пересечения для случаю двух подпространств дает специальная теорема.
Теорема 5.6 (Грассман).
Пусть  и
и 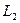 – подпространства конечномерного пространства. Тогда имеет место формула
– подпространства конечномерного пространства. Тогда имеет место формула
 .
.
Доказательство. Будем считать, что 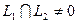 (в противном случае доказательство протекает по той же схеме, но проще). И пусть
(в противном случае доказательство протекает по той же схеме, но проще). И пусть  будет базисом пересечения. Тогда в соответствии с леммой 5.14 эту систему можно дополнить до базиса
будет базисом пересечения. Тогда в соответствии с леммой 5.14 эту систему можно дополнить до базиса  и базиса
и базиса 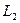 , так как
, так как 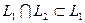 и
и 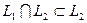 . Пусть система
. Пусть система 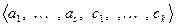 будет базисом
будет базисом  , а
, а  будет базисом
будет базисом 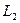 . Построим объединенную систему
. Построим объединенную систему 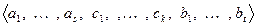 . Если доказать, что эта система является базисом суммы, то теорема будет доказана. В самом деле,
. Если доказать, что эта система является базисом суммы, то теорема будет доказана. В самом деле, 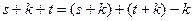 . Легко видеть, что каждый вектор суммы линейно выражается через объединенную систему. Поэтому, в соответствии определением базиса, осталось доказать линейную независимость системы. Применим критерий линейной независимости. Построим линейную комбинацию векторов системы и приравняем ее нулю. Если покажем, что в таком случае должны быть равны нулю все коэффициенты линейной комбинации, то
. Легко видеть, что каждый вектор суммы линейно выражается через объединенную систему. Поэтому, в соответствии определением базиса, осталось доказать линейную независимость системы. Применим критерий линейной независимости. Построим линейную комбинацию векторов системы и приравняем ее нулю. Если покажем, что в таком случае должны быть равны нулю все коэффициенты линейной комбинации, то
система оказывается линейно независимой. Действительно, пусть
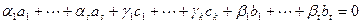 .
.
Вектор 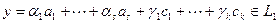 , а вектор
, а вектор 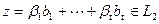 , но
, но 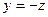 , поэтому
, поэтому 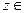
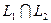 , и, следовательно, может быть разложен по базису пересечения
, и, следовательно, может быть разложен по базису пересечения  , т.е.,
, т.е., 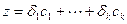 . Тогда имеем:
. Тогда имеем:

 . Откуда
. Откуда 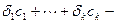
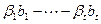
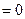 . Получили линейную комбинацию векторов базиса
. Получили линейную комбинацию векторов базиса 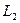 , равную нулю. Следовательно, по критерию линейной независимости все коэффициенты комбинации равны нулю. Таким образом, заведомо
, равную нулю. Следовательно, по критерию линейной независимости все коэффициенты комбинации равны нулю. Таким образом, заведомо 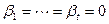 . Но тогда от исходной линейной комбинации остается
. Но тогда от исходной линейной комбинации остается
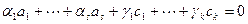 .
.
Теперь получаем линейную комбинацию базисных векторов  , равную нулю. Поэтом и ее коэффициенты раны нулю, что и завершает доказательство теоремы.
, равную нулю. Поэтом и ее коэффициенты раны нулю, что и завершает доказательство теоремы.
Пример 5.16. Пусть заданы линейные оболочки 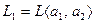 и
и 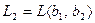 , где
, где 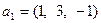 ,
, 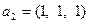 ,
, 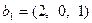 ,
, 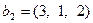 . Требуется найти сумму и пересечение
. Требуется найти сумму и пересечение  и
и 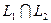 . Очевидно, что суммой подпространств будет линейная оболочка, построенная на объединенной системе
. Очевидно, что суммой подпространств будет линейная оболочка, построенная на объединенной системе 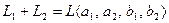 . Так как база системы является базисом соответствующей линейной оболочки, то ранг системы становится размерностью линейной оболочки. Вычисляя базу и ранг этой объединенной системы получаем, что базу составляют, например,
. Так как база системы является базисом соответствующей линейной оболочки, то ранг системы становится размерностью линейной оболочки. Вычисляя базу и ранг этой объединенной системы получаем, что базу составляют, например, 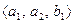 , а ранг равен 3, т.е.,
, а ранг равен 3, т.е., 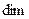
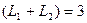 , а
, а  . Поэтому по формуле Грассмана
. Поэтому по формуле Грассмана 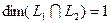 . Значит,
. Значит, 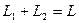
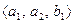 . Далее, составляя векторное равенство
. Далее, составляя векторное равенство 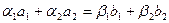 и переходя к решению системы линейных уравнений, получим, что, например,
и переходя к решению системы линейных уравнений, получим, что, например,  . Это и в первом и во втором случае дает вектор пересечения
. Это и в первом и во втором случае дает вектор пересечения 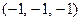 , что означает
, что означает 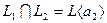 .
.
Определение 5.17. Сумма 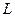 подпространств
подпространств 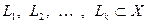 называется прямой, если каждый вектор суммы
называется прямой, если каждый вектор суммы 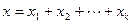 , где
, где  ,
,  , однозначно представляется указанным образом. Обозначение для прямой суммы следующее:
, однозначно представляется указанным образом. Обозначение для прямой суммы следующее:
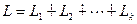 .
.
Единственность представления векторов в прямой сумме напоминает разложение по базису. Таким образом, прямая сумма в этом смысле предоставляет описание векторов через «обобщенный базис».
Определение 5.18. Пусть пространство Х разложено в прямую сумму двух подпространств, именно: 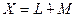 . Тогда М называется прямым дополнением к
. Тогда М называется прямым дополнением к 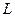 в Х.
в Х.
Непосредственно увидеть единственность представления векторов суммы зачастую трудно. Поэтому следующий критерий прямой суммы позволяет взглянуть на это понятие с другой стороны.
Теорема 5.7 (первый критерий прямой суммы).
Сумма подпространств 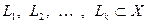 будет прямой тогда и только тогда, когда объединение базисов подпространств-слагаемых составляет базис суммы.
будет прямой тогда и только тогда, когда объединение базисов подпространств-слагаемых составляет базис суммы.
Доказательство. Необходимость. Пусть сумма прямая: 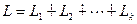 . Зададим базисы подпространств-слагаемых. Положим
. Зададим базисы подпространств-слагаемых. Положим 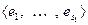 – базис
– базис  ,
, 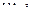
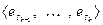 – базис
– базис 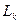 . Объединим базисы в одну систему и докажем ее линейную независимость. Доказательство же представимости векторов суммы через объединенную систему очевидно. Построим линейную комбинацию системы и приравняем ее нулю:
. Объединим базисы в одну систему и докажем ее линейную независимость. Доказательство же представимости векторов суммы через объединенную систему очевидно. Построим линейную комбинацию системы и приравняем ее нулю:
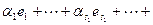
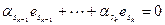 .
.
Введем обозначения: 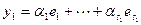 ,
, 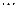 ,
, 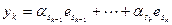 . Тогда получим, что
. Тогда получим, что 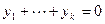 , где
, где 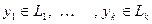 . Нулевой вектор, очевидно, принадлежит сумме и всегда имеет тривиальное представление
. Нулевой вектор, очевидно, принадлежит сумме и всегда имеет тривиальное представление 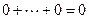 . Таким образом, в силу прямоты суммы получаем, что
. Таким образом, в силу прямоты суммы получаем, что 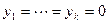 . Но тогда по критерию линейной независимости все коэффициенты линейных комбинаций, представляющих векторы
. Но тогда по критерию линейной независимости все коэффициенты линейных комбинаций, представляющих векторы 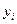 ,
,  , через базисы подпространств-слагаемых, равны нулю. То есть, все коэффициенты исходной линейной комбинации равны нулю. Применение критерия линейной независимости завершает доказательство необходимости.
, через базисы подпространств-слагаемых, равны нулю. То есть, все коэффициенты исходной линейной комбинации равны нулю. Применение критерия линейной независимости завершает доказательство необходимости.
Достаточность. Пусть теперь введенные выше базисные системы составляют в объединении базис суммы. Значит, любой вектор суммы 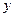 представляется через этот базис:
представляется через этот базис: 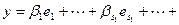
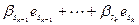 . По свойству базиса (см. лемму 5.12) это представление единственно. Как вектор суммы
. По свойству базиса (см. лемму 5.12) это представление единственно. Как вектор суммы 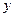 представляется в виде:
представляется в виде: 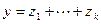 , где
, где 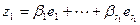 ,
, 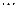 ,
, 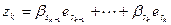 . Если бы указанный вектор, как вектор суммы, мог быть представлен иначе, то это сразу бы отразилось на представлении слагаемых в соответствии с той же леммой 5.12. Что сразу приводит к противоречию. Теорема доказана.
. Если бы указанный вектор, как вектор суммы, мог быть представлен иначе, то это сразу бы отразилось на представлении слагаемых в соответствии с той же леммой 5.12. Что сразу приводит к противоречию. Теорема доказана.
Пример 5.17.Пусть задано линейное пространство в виде линейной оболочки 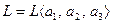 , где
, где 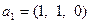 ,
, 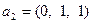 ,
, 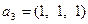 . Легко видеть, что указанная система линейно независима, т.е., представляет собой базис линейной оболочки. Разобьем ее на две подсистемы
. Легко видеть, что указанная система линейно независима, т.е., представляет собой базис линейной оболочки. Разобьем ее на две подсистемы 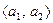 и
и  . Тогда получим разложение
. Тогда получим разложение 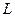 в прямую сумму:
в прямую сумму: 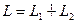 , где
, где 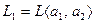 , а
, а 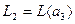 . Здесь каждое слагаемое является прямым дополнением ко второму в
. Здесь каждое слагаемое является прямым дополнением ко второму в 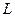 .
.
Теорема 5.8 (второй критерий прямой суммы).
Сумма подпространств будет прямой тогда и только тогда, когда пересечение каждого из слагаемых с суммой остальных нулевое.
Доказательство. Необходимость. Пусть задана прямая сумма 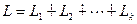 . И пусть, например,
. И пусть, например, 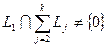 . Тогда это пересечение содержит ненулевой вектор
. Тогда это пересечение содержит ненулевой вектор 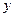 , который может быть представлен двумя различными способами как вектор суммы. Действительно, так как
, который может быть представлен двумя различными способами как вектор суммы. Действительно, так как  , то
, то 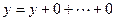 , но
, но 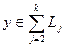 , т.е., представляется в виде
, т.е., представляется в виде 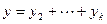 , а как вектор полной суммы в виде
, а как вектор полной суммы в виде 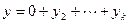 , что противоречит определению прямой суммы.
, что противоречит определению прямой суммы.
Достаточность. Пусть теперь 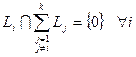 ,
,  . Снова рассуждаем от противного. Предположим, что при этом сумма не является прямой. Это значит, что существует вектор y в сумме, представляющийся неоднозначно в виде
. Снова рассуждаем от противного. Предположим, что при этом сумма не является прямой. Это значит, что существует вектор y в сумме, представляющийся неоднозначно в виде 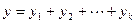 , где
, где 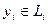 ,
,  . Например, пусть еще
. Например, пусть еще 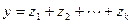 . Вычитая из первого равенства второе, получим
. Вычитая из первого равенства второе, получим 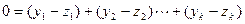 . Так как
. Так как 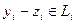 ,
,  , то это равенство представляет вектор 0 как вектор суммы. И пусть
, то это равенство представляет вектор 0 как вектор суммы. И пусть 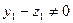 . Тогда
. Тогда 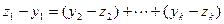 , т.е., ненулевой вектор из
, т.е., ненулевой вектор из  принадлежит сумме
принадлежит сумме 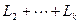 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Следствие 1. Сумма двух подпространств 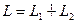 будет прямой тогда и только тогда, когда
будет прямой тогда и только тогда, когда  .
.
Следствие 2. 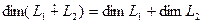 .
.
Изоморфизм линейных пространств
При изучении алгебраических структур легко заметить известны параллелизм свойств, связанных с операциями. Это касается и линейных пространств. Для наведения определенного порядка в бесконечной совокупности пространств изобретен специальный инструмент. Его называют изоморфизмом ЛП.
Определение 5.19. Пусть заданы два линейных пространства над одним и тем же полем 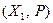 и
и 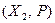 . Изоморфизмом из
. Изоморфизмом из 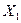 в
в 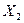 называется биекция
называется биекция
| <== предыдущая лекция | | | следующая лекция ==> |
| Кооперативная теория | | |
Дата добавления: 2019-07-26; просмотров: 593;
