Функция распределения двумерной случайной величины и ее свойства
Универсальной формой задания распределения двумерной случайной величины является функция распределения (или «интегральная функция»), пригодная как для дискретной, так и для непрерывной случайной величины, обозначаемая 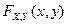 или просто
или просто 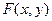 .
.
Функцией распределения двумерной случайной величины  называется функция
называется функция 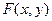 , которая для любых действительных чисел х и у равна вероятности совместного выполнения двух событий
, которая для любых действительных чисел х и у равна вероятности совместного выполнения двух событий 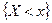 и
и 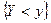 .
.
Таким образом, по определению
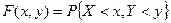
| (6.2) |
событие 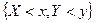 означает произведение событий
означает произведение событий 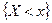 и
и 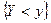 .
.
Геометрически функция 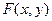 интерпретируется как вероятность попадания случайной точки
интерпретируется как вероятность попадания случайной точки  в бесконечный квадрант с вершиной в точке
в бесконечный квадрант с вершиной в точке 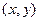 , лежащий левее и ниже ее (рис. 6.2).
, лежащий левее и ниже ее (рис. 6.2).
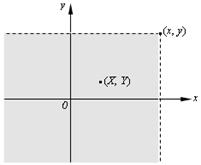
Рис. 6.2.
Функция распределения двумерной дискретной случайной величины  находится суммированием всех вероятностей
находится суммированием всех вероятностей 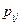 , для которых
, для которых 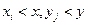 , т.е.
, т.е.
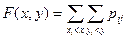 . .
| (6.3) |
Геометрическая интерпретация функции распределения позволяет наглядно иллюстрировать ее свойства.
Свойства функции распределения двумерной случайной величины:
1. Функция распределения 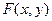 ограничена, т.е.
ограничена, т.е.
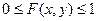
2. 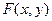 не убывает по каждому из своих аргументов при фиксированном другом, т.е.
не убывает по каждому из своих аргументов при фиксированном другом, т.е.
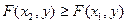 при
при 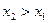
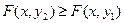 при
при 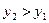
3. Если хотя бы один из аргументов обращается в 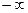 , то функция распределения
, то функция распределения 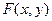 равна нулю, т.е.
равна нулю, т.е.
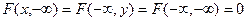
4. Если оба аргумента обращаются в 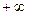 , то
, то 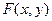 равна 1, т.е.
равна 1, т.е.
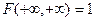 .
.
5. Если один из аргументов обращается в 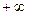 , то функция распределения системы случайных величин становится функцией распределения случайной величины, соответствующей другому элементу, т.е.
, то функция распределения системы случайных величин становится функцией распределения случайной величины, соответствующей другому элементу, т.е.
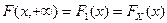 , , 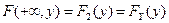 . .
| (6.4) |
6. 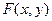 непрерывна слева по каждому из своих аргументов, т.е.
непрерывна слева по каждому из своих аргументов, т.е.
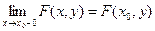 ,
, 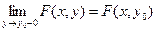
Зная совместное распределение двух случайных величин X и Y, можно найти одномерные распределения этих случайных величин, но обратное, вообще говоря, неверно.
Отметим, что с геометрической точки зрения 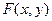 есть некоторая поверхность (ступенчатая для двумерной дискретной случайной величины), обладающая указанными свойствами.
есть некоторая поверхность (ступенчатая для двумерной дискретной случайной величины), обладающая указанными свойствами.
С помощью функции 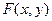 легко можно найти вероятность попадания случайной точки
легко можно найти вероятность попадания случайной точки  в прямоугольникD со сторонами, параллельными координатным осям:
в прямоугольникD со сторонами, параллельными координатным осям:
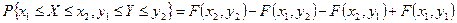 . .
| (6.5) |
Приведем геометрическое доказательство (рис. 6.3)
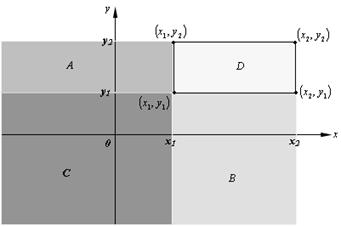
Рис. 6.3.
Здесь 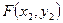 - вероятность попадания случайной точки в область D,
- вероятность попадания случайной точки в область D, 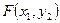 - в А,
- в А, 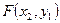 - в В,
- в В, 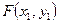 - в С (эту область дважды вычли, следует один раз прибавить).
- в С (эту область дважды вычли, следует один раз прибавить).
Пример 6.2.По таблицам распределения системы  компонент X и Y примера 6.1. найти
компонент X и Y примера 6.1. найти 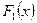 ,
, 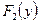 ,
, 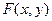 .
.
Решение:
Используя формулу (6.4), находим функцию распределения 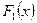 ,
, 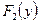 ,
,
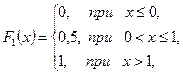
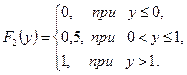
Используя формулу (6.3.), находим функцию распределения 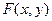 :
:
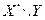
| 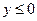
| 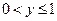
| 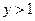
|
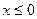
| |||
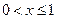
| 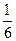
| 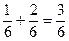
| |
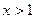
| 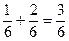
| 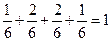
|
Дата добавления: 2017-03-29; просмотров: 200;
