Теоретическое определение коэффициента местного сопротивления при внезапном расширении потока
В этом частном случае коэффициент местного сопротивления можно определить теоретически, что представляет интерес с точки зрения установления его природы.
На рис. 9.5 представлен случай, когда труба диаметром 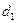 переходит в трубу с большим диаметром
переходит в трубу с большим диаметром 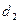 . Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2-2 заполняет все сечение второй трубы. Расширение струи сопровождается отрывом ее от стенок и образованием водоворотной зоны, имеющей кольцевую форму.
. Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2-2 заполняет все сечение второй трубы. Расширение струи сопровождается отрывом ее от стенок и образованием водоворотной зоны, имеющей кольцевую форму.
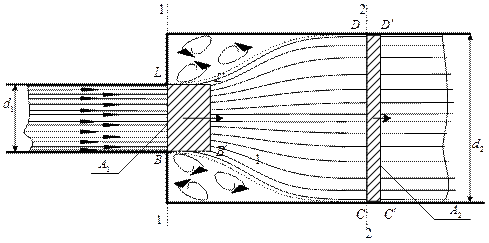 Рис. 9.4
Рис. 9.4
|
Для определения потери напора запишем уравнение Бернулли для сечений 1-1 и 2-2, принимая во внимание горизонтальность расположения оси канала.
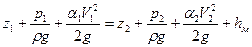 . .
| (9.5) |
Принимая 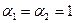 , из (9.5) получаем
, из (9.5) получаем
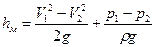 . .
| (9.6) |
Разность давлений найдем используя теорему механики об изменении количества движения массы жидкости , содержащейся в объеме между сечениями 1-1 и 2-2. Пусть за время 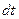 объем LBCD переместится в положение
объем LBCD переместится в положение 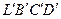 . Так как жидкость предполагаем несжимаемой, объемы жидкости, прошедшие через сечения 1-1 и 2-2 за время
. Так как жидкость предполагаем несжимаемой, объемы жидкости, прошедшие через сечения 1-1 и 2-2 за время 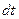 одинаковы. На рис. 9.4 они заштрихованы
одинаковы. На рис. 9.4 они заштрихованы 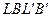 =
= 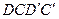 . Очевидно, что изменение количества движения массы жидкости в объеме LBCD определяется изменением количества движения массы жидкости в объемах
. Очевидно, что изменение количества движения массы жидкости в объеме LBCD определяется изменением количества движения массы жидкости в объемах 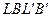 и
и 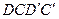 . Количество движения массы жидкости в объеме
. Количество движения массы жидкости в объеме 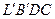 за время
за время 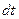 осталось без изменения.
осталось без изменения.
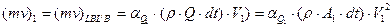 ; ;
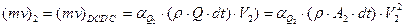 , ,
| (9.7) |
где 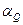 -- коэффициент, корректирующий расчет количества движения через среднюю скорость в сечении.
-- коэффициент, корректирующий расчет количества движения через среднюю скорость в сечении.
Изменение количества движения выделенного объема за время 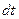 составит
составит
 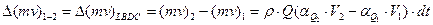 . .
| (9.8) |
При определении импульса сил, действующих на выделенный объем, не будем принимать во внимание силы трения между стенками трубы и жидкостью. Ось трубы предполагаем горизонтальной, поэтому импульс сил тяжести и сил давления боковых стенок на эту ось равны нулю. Импульсы других сил:
силы давления на выделенный объем в сечении 2-2
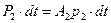 , ,
| (9.9) |
силы давления на выделенный объем в сечении 1-1 со стороны жидкости в трубе диаметром 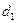 и кольцевой стенки трубопровода, расположенных слева от него
и кольцевой стенки трубопровода, расположенных слева от него
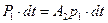 . .
| (9.10) |
С учетом (9.8), (9.9), (9.10) теорема об изменении количества движения в проекции на ось потока запишется так
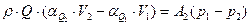  
| (9.11) |
Сохраняя качественный характер анализа, принимаем 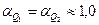 (в действительности при параболическом законе изменения локальной скорости по радиусу сечения потока
(в действительности при параболическом законе изменения локальной скорости по радиусу сечения потока 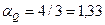 ). Так как
). Так как 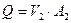 из (9.11) находим
из (9.11) находим
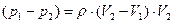 . . 
| (9.12) |
Подстановка (9.12) в выражение (9.7) позволяет найти формулу для определения потери напора на рассматриваемом местном сопротивлении
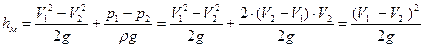 , , 
| (9.13) |
где 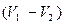 - называют потерянной скоростью.
- называют потерянной скоростью.
Формула (9.13) называется формулой 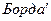 . Согласно ей потеря напора при резком расширении потока равняется скоростному напору, соответствующему потерянной скорости.
. Согласно ей потеря напора при резком расширении потока равняется скоростному напору, соответствующему потерянной скорости.
Если изменить форму записи (9.13), то можно установить теоретическое значение коэффициента местных потерь для рассматриваемого случая
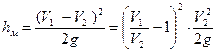 , , 
|
следовательно
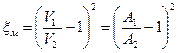 . . 
| (9.14) |
Следует заметить, что действительные потери напора на этом местном сопротивлении несколько больше, чем дает использование формулы (9.14) (см. допущение 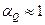 и др.).
и др.).
Табл. 9.2
Для соединения труб при 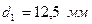
| ||||||||||
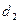 , мм , мм
| 39,5 | 37,5 | 35,3 | 33,06 | 30,6 | 27,95 | 25,0 | 21,65 | 17,68 | 12,5 |
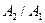
| ||||||||||
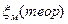
| 1,0 | |||||||||
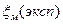
| 98,6 | 75,2 | 55,7 | 39,7 | 26,9 | 16,8 | 9,3 | 4,1 | 1,017 | |
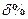
| 2,5 | 1,76 |
Тем не менее, полученный результат достаточно хорошо подтверждается экспериментальными исследованиями (табл. 9.2), где максимальное расхождение в величине коэффициента местного сопротивления достигает 21% при десятикратном увеличении площади поперечного сечения.
Дата добавления: 2017-12-07; просмотров: 1762;
