Уравнение Бернулли для струйки в криволинейном канале, вращающемся с постоянной угловой скоростью

В том случая, когда жидкость движется в криволинейном канале, вращающемся с постоянной угловой скоростью, и линия действия силы тяжести параллельна оси вращения канала (рис.6.4), массовые силы, включая силу инерции в переносном движении, отнесенные к единице массы равны

.

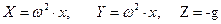(6.36)

Здесь учтены силы инерции в переносном движении, связанные с нормальным ускорением и сила тяжести. Сила инерции, определяемая кориолисовым ускорением, не рассматривается, т.к. она не влияет на движение частицы жидкости в направлении ее относительного движения.

Тогда, полагая

,

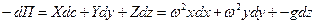(6.37)

после интегрирования найдем потенциал массовых сил

,

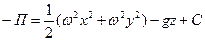(6.38)

или

.

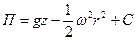(6.39)

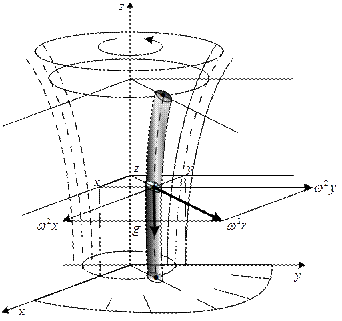Рис.6.4

Уравнение Бернулли (6.15) принимает вид

,

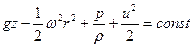(6.40)

или

.

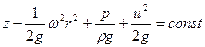(6.41)

Для двух сечений элементарной струйки можно записать

.

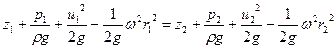(6.42)

Здесь 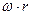есть угловая скорость в переносном движении.

Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости

Каждое слагаемое в уравнении (6.34) можно рассматривать, как составляющую энергии частицы, отнесенную к единице веса.

Если за плоскость сравнения принять плоскость с нулевой потенциальной энергией, то:

- потенциальная энергия единицы веса определится формулой

;

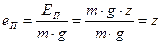(6.42)

- удельная кинетическая энергия составит

;

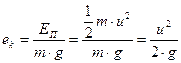(6.42)

- удельная энергия давления будет равна

.

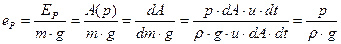(6.42)

Для удельной энергии и ее составляющих, в гидравлике применяют следующие термины и обозначения:

H - гидродинамический или полный напор;

z - геометрический напор;

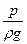- пьезометрический напор;

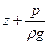- гидростатический напор;

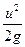- скоростной или кинетический напор.

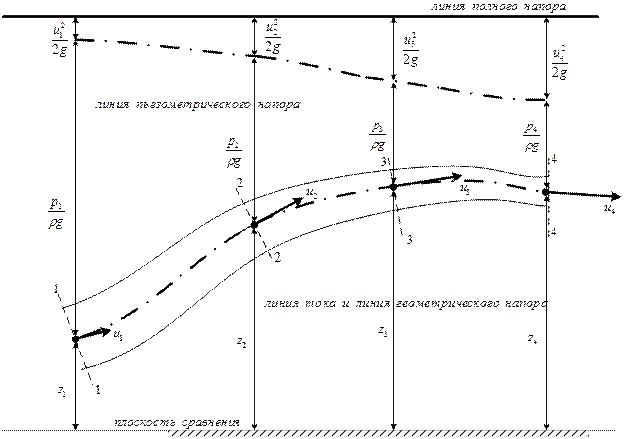
Рис. 6.5. Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости.

Единицей измерения напора является единица длины. Ясно, что при движении идеальной жидкости отдельные составляющие полного напора могут изменяться, но полный напор остается величиной постоянной (рис. 6.5).