Теоретические сведения

 Фильтры СВЧ проектируются на основе «прототипных» фильтров, которые представляют собой фильтры на сосредоточенных элементах, АЧХ и ФЧХ которых совпадают с таковыми для разрабатываемых фильтров СВЧ. Прототипные фильтры имеют такое же характеристическое сопротивление, что и фильтры СВЧ и могут проектироваться как расчетным путем [3]‒[5], так и с помощью программных средств. Фильтр СВЧ создается путем замены сосредоточенных элементов прототипного фильтра отрезками тех или иных ЛП, импедансы которых были бы равны импедансам сосредоточенных элементов. К сожалению, частотные зависимости импедансов сосредоточенных элементов (индуктивностей и емкостей) отличаются от таковых для отрезков линий передачи, и необходимое их равенство может быть достигнуто только в ограниченной частотной области. При замене необходимо выбирать параметры отрезков так, чтобы минимизировать это несоответствие. Далее рассмотрено проектирование фильтров нижних частот (ФНЧ) СВЧ и полосно-пропускающих фильтров (ППФ) СВЧ.
Фильтры СВЧ проектируются на основе «прототипных» фильтров, которые представляют собой фильтры на сосредоточенных элементах, АЧХ и ФЧХ которых совпадают с таковыми для разрабатываемых фильтров СВЧ. Прототипные фильтры имеют такое же характеристическое сопротивление, что и фильтры СВЧ и могут проектироваться как расчетным путем [3]‒[5], так и с помощью программных средств. Фильтр СВЧ создается путем замены сосредоточенных элементов прототипного фильтра отрезками тех или иных ЛП, импедансы которых были бы равны импедансам сосредоточенных элементов. К сожалению, частотные зависимости импедансов сосредоточенных элементов (индуктивностей и емкостей) отличаются от таковых для отрезков линий передачи, и необходимое их равенство может быть достигнуто только в ограниченной частотной области. При замене необходимо выбирать параметры отрезков так, чтобы минимизировать это несоответствие. Далее рассмотрено проектирование фильтров нижних частот (ФНЧ) СВЧ и полосно-пропускающих фильтров (ППФ) СВЧ.
Рассмотрим выбор параметров отрезков ЛП на примере ФНЧ третьего порядка, схема прототипа которого приведена на рис. 7.1. Здесь R1 – характеристическое сопротивление фильтра, С1= С2 = С;


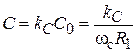 ,
, 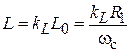 ,
, 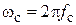 ‒ частота среза, коэффициенты
‒ частота среза, коэффициенты 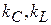 обеспечивают ту или иную полиномиальную характеристику (Баттерворта, Чебышева и др.) фильтра. Параллельное соединение C2 и R1 обозначим
обеспечивают ту или иную полиномиальную характеристику (Баттерворта, Чебышева и др.) фильтра. Параллельное соединение C2 и R1 обозначим 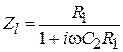 . Тогда сопротивление на входном (левом) конце индуктивности (без учета емкости
. Тогда сопротивление на входном (левом) конце индуктивности (без учета емкости 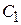 ) будет равно
) будет равно 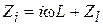 . Заменим индуктивность отрезком ЛП TL1 с волновым сопротивлением
. Заменим индуктивность отрезком ЛП TL1 с волновым сопротивлением 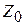 , включен- ным последовательно нагрузке (рис. 7.2) ; входное сопротивление
, включен- ным последовательно нагрузке (рис. 7.2) ; входное сопротивление 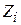 будет равно:
будет равно: 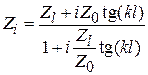 (здесь
(здесь 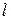 ‒ геометрическая длина отрезка,
‒ геометрическая длина отрезка, 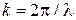 ). Очевидно несоответствие между обоими выражениями. Приближенное соответствие может быть получено, если минимизировать второе слагаемое в знаменателе последней формулы. Это можно сделать, уменьшив значение тангенса и увеличив значение
). Очевидно несоответствие между обоими выражениями. Приближенное соответствие может быть получено, если минимизировать второе слагаемое в знаменателе последней формулы. Это можно сделать, уменьшив значение тангенса и увеличив значение 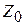 по сравнению с
по сравнению с 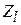 . Уменьшение
. Уменьшение 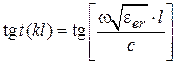 (здесь
(здесь 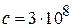 ‒ скорость света в свободном пространстве,
‒ скорость света в свободном пространстве, 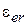 ‒ относительная эффективная диэлектрическая проницаемость для ЛП) положительно скажется на частотных характеристиках ФНЧ, так как, благодаря малости аргумента, функция тангенса в области полосы пропускания фильтра будет почти линейно зависеть от частоты. Если принять значение аргумента равным 0.3, то значение тангенса будет равно 0.3093, т. е. отличаться от аргумента на 3 %. При уменьшении частоты (в области полосы пропускания ФНЧ) тангенс будет изменяться практически линейно. На частоте среза можно записать равенство:
‒ относительная эффективная диэлектрическая проницаемость для ЛП) положительно скажется на частотных характеристиках ФНЧ, так как, благодаря малости аргумента, функция тангенса в области полосы пропускания фильтра будет почти линейно зависеть от частоты. Если принять значение аргумента равным 0.3, то значение тангенса будет равно 0.3093, т. е. отличаться от аргумента на 3 %. При уменьшении частоты (в области полосы пропускания ФНЧ) тангенс будет изменяться практически линейно. На частоте среза можно записать равенство: 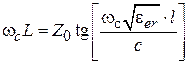 . На этой частоте
. На этой частоте 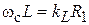 и
и 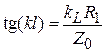 . Оценим значение второго слагаемого в знаменателе выражения для
. Оценим значение второго слагаемого в знаменателе выражения для 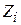 на частоте среза:
на частоте среза: 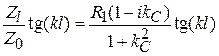 . Модуль этого слагаемого равен
. Модуль этого слагаемого равен 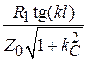 ; подставив сюда значение тангенса, получим:
; подставив сюда значение тангенса, получим: 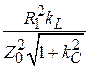 . Минимальное значение
. Минимальное значение 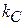 порядка единицы, максимальное значение
порядка единицы, максимальное значение 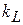 порядка двух. Тогда модуль будет примерно равен
порядка двух. Тогда модуль будет примерно равен 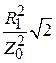 . Потребуем, чтобы его значение было бы равно 0.1, при этом модуль знаменателя будет отличен от единицы на 10 %. Отсюда оценка для волнового сопротивления:
. Потребуем, чтобы его значение было бы равно 0.1, при этом модуль знаменателя будет отличен от единицы на 10 %. Отсюда оценка для волнового сопротивления: 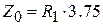 . Таким образом, волновое сопротивление последовательной линии, заменяющей индуктивность, надо выбирать по правилу
. Таким образом, волновое сопротивление последовательной линии, заменяющей индуктивность, надо выбирать по правилу 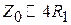 . Перейдем теперь к параллельным реактивностям. Они имеют емкостный характер и при замене их на отрезки ЛП (разомкнутые на конце и с
. Перейдем теперь к параллельным реактивностям. Они имеют емкостный характер и при замене их на отрезки ЛП (разомкнутые на конце и с 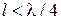 ) должно выполняться приближенное равенство:
) должно выполняться приближенное равенство: 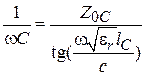 ;
; 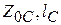 ‒ волновое сопротивление и геометрическая длина этих отрезков. Для обеспечения линейности частотной оси примем аргумент тангенса равным 0.3 и потребуем выполнения равенства на частоте среза
‒ волновое сопротивление и геометрическая длина этих отрезков. Для обеспечения линейности частотной оси примем аргумент тангенса равным 0.3 и потребуем выполнения равенства на частоте среза 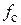 . Отсюда получаем выражение:
. Отсюда получаем выражение: 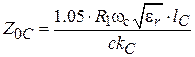 . Длина отрезка линии определится выражением
. Длина отрезка линии определится выражением 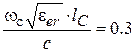 . Полагая частоту в ГГц, получим длину линии, мм:
. Полагая частоту в ГГц, получим длину линии, мм: 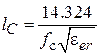 . Подставив это значение в формулу для
. Подставив это значение в формулу для 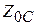 получим:
получим: 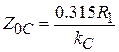 . Таким образом, волновое сопротивление отрезка линии передачи, заменяющего емкость, примерно в 3 раза меньше характеристического сопротивления ФНЧ. Необходимо иметь в виду, что
. Таким образом, волновое сопротивление отрезка линии передачи, заменяющего емкость, примерно в 3 раза меньше характеристического сопротивления ФНЧ. Необходимо иметь в виду, что 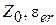 различны для последовательного и параллельных отрезков ЛП. При выборе волнового сопротивления параллельного отрезка в соответствии с приведенным критерием его ширина становится больше длины и четкой структуры ФНЧ не получается. Удобно использовать в качестве емкостей отрезки секториальной ЛП, которые подсоединяются к концам ЛП остриями сектора, что позволяет точно локализовать место подключения. Приближенно емкость такого отрезка можно оценить как
различны для последовательного и параллельных отрезков ЛП. При выборе волнового сопротивления параллельного отрезка в соответствии с приведенным критерием его ширина становится больше длины и четкой структуры ФНЧ не получается. Удобно использовать в качестве емкостей отрезки секториальной ЛП, которые подсоединяются к концам ЛП остриями сектора, что позволяет точно локализовать место подключения. Приближенно емкость такого отрезка можно оценить как 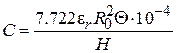 , где
, где 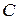 ‒ емкость в пФ;
‒ емкость в пФ; 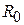 ‒ радиус секториального отрезка;
‒ радиус секториального отрезка; 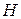 ‒ толщина подложки в см;
‒ толщина подложки в см; 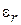 ‒ относительная диэлектрическая проницаемость подложки;
‒ относительная диэлектрическая проницаемость подложки; 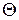 ‒ угол раскрыва отрезка в …°. При заданной емкости значение радиуса можно оценить как
‒ угол раскрыва отрезка в …°. При заданной емкости значение радиуса можно оценить как 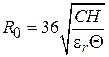 . Если воспользоваться значением
. Если воспользоваться значением 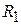 характеристического сопротивления ФНЧ, то
характеристического сопротивления ФНЧ, то 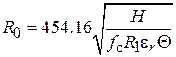 , где
, где 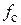 ‒ частота среза ФНЧ в ГГц.
‒ частота среза ФНЧ в ГГц.
Проектирование ФНЧ
Для проверки применимости предлагаемого подхода к проектированию СВЧ ФНЧ рассмотрим конкретный пример фильтра третьего порядка с характеристикой Баттерворта в виде П-структуры со следующими параметрами: 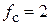 ГГц,
ГГц, 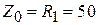 Ом,
Ом, 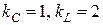 ,
, 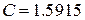 пФ,
пФ, 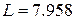 нГн. Для перехода к СВЧ ФНЧ примем для отрезка ЛП, заменяющего индуктивность,
нГн. Для перехода к СВЧ ФНЧ примем для отрезка ЛП, заменяющего индуктивность, 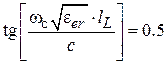 . Модуль сопротивления индуктивности на частоте среза равен
. Модуль сопротивления индуктивности на частоте среза равен 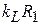 =100 Ом и, при волновом сопротивлении отрезка 200 Ом (см. ниже)
=100 Ом и, при волновом сопротивлении отрезка 200 Ом (см. ниже) 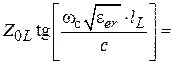 100 Ом. Выберем толщину подложки Н = 4 мм, ее относительную диэлектрическую проницаемость
100 Ом. Выберем толщину подложки Н = 4 мм, ее относительную диэлектрическую проницаемость 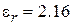 ,
,
 волновое сопротивление отрезка
волновое сопротивление отрезка 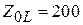 Ом и с помощью калькулятора TXLine из пакета MWO найдем ширину отрезка
Ом и с помощью калькулятора TXLine из пакета MWO найдем ширину отрезка 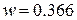 мм и относительную диэлектрическую проницаемость для отрезка
мм и относительную диэлектрическую проницаемость для отрезка 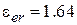 . Аргумент тангенса равен 26.565°, откуда следует, что длина отрезка
. Аргумент тангенса равен 26.565°, откуда следует, что длина отрезка 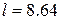 мм. Определим размеры подводящей микрополосковой ЛП с волновым сопротивлением 50 Ом. Получаем ширину полоска
мм. Определим размеры подводящей микрополосковой ЛП с волновым сопротивлением 50 Ом. Получаем ширину полоска 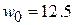 мм. Рассчитаем приближенное значение радиуса секториальной линии, обеспечивающее расчетное значение емкости:
мм. Рассчитаем приближенное значение радиуса секториальной линии, обеспечивающее расчетное значение емкости: 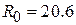 мм. На частоте среза модуль реактивного сопротивления емкостей равен
мм. На частоте среза модуль реактивного сопротивления емкостей равен 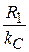 = 50 Ом, а проводимость равна 0.02 См. Запустим программу MWO, откроем проект Sector, зададим в меню Options/Project Options/Frequency интервал изменения частоты от 1.8 до 2.2 ГГц с шагом 0.1 ГГц, затем создадим схему, изображенную на рис. 7.3. В левой части схемы расположена иконка подложки с названием MSUB, находящаяся в закладке Elements/Substrates. Ее перетаскивают на схему, вносят в надпись параметры подложки, в правой части расположена схема, состоящая из порта и иконок «земли» и секториальной линии под названием MRSTUB2, которая находится в Elements/Microstrip/Other.
= 50 Ом, а проводимость равна 0.02 См. Запустим программу MWO, откроем проект Sector, зададим в меню Options/Project Options/Frequency интервал изменения частоты от 1.8 до 2.2 ГГц с шагом 0.1 ГГц, затем создадим схему, изображенную на рис. 7.3. В левой части схемы расположена иконка подложки с названием MSUB, находящаяся в закладке Elements/Substrates. Ее перетаскивают на схему, вносят в надпись параметры подложки, в правой части расположена схема, состоящая из порта и иконок «земли» и секториальной линии под названием MRSTUB2, которая находится в Elements/Microstrip/Other.

 В надпись вносится рассчитанный радиус
В надпись вносится рассчитанный радиус 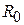 , радиус
, радиус 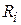 , отсчитываемый от начала (острия) секториальной линии, при котором длина хорды равна ширине
, отсчитываемый от начала (острия) секториальной линии, при котором длина хорды равна ширине 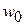 подводящей 50-омной микрополосковой линии (в данном случае
подводящей 50-омной микрополосковой линии (в данном случае 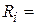 8.84 мм) и угол раскрыва линии Theta, равный 90°. Далее заказываем измерение входной реактивной проводимости схемы, которая оказывается равной 0.034 на частоте 2 ГГц. Необходимая проводимость равна 0.02, и поэтому радиус
8.84 мм) и угол раскрыва линии Theta, равный 90°. Далее заказываем измерение входной реактивной проводимости схемы, которая оказывается равной 0.034 на частоте 2 ГГц. Необходимая проводимость равна 0.02, и поэтому радиус 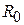 должен быть уменьшен в
должен быть уменьшен в 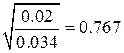 раз – до 15.8 мм. Расчет при этом значении дает меньшую проводимость. После нескольких коррекций получаем точное значение ‒ 17.45 мм. Теперь открываем новый проект LPF, в котором построим схему фильтра, изображенного на рис. 7.4. Здесь линии TL1, TL2 ‒ 50-омные отрезки МПЛ для соединения ФНЧ с портами; линия TL3 ‒ эквивалент индуктивности; TL4 и TL5 ‒ эквиваленты емкостей. После этого создаем схему прототипного ФНЧ на сосредоточенных элементах, изображенную на рис. 7.5, и называем ее Lumped LPF. Далее заказываем график в Project/ Add Graph в прямоугольных координатах, который назовем
раз – до 15.8 мм. Расчет при этом значении дает меньшую проводимость. После нескольких коррекций получаем точное значение ‒ 17.45 мм. Теперь открываем новый проект LPF, в котором построим схему фильтра, изображенного на рис. 7.4. Здесь линии TL1, TL2 ‒ 50-омные отрезки МПЛ для соединения ФНЧ с портами; линия TL3 ‒ эквивалент индуктивности; TL4 и TL5 ‒ эквиваленты емкостей. После этого создаем схему прототипного ФНЧ на сосредоточенных элементах, изображенную на рис. 7.5, и называем ее Lumped LPF. Далее заказываем график в Project/ Add Graph в прямоугольных координатах, который назовем 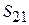 .
.



 Затем заказываем измерение Project/Add Measurement; в открывшемся окне выбираем
Затем заказываем измерение Project/Add Measurement; в открывшемся окне выбираем 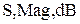 , в окошке Data Source Name выбираем LPF, в окошке To Port Index выбираем 2, в окошке From Port Index выбираем 1, нажимаем ОК и затем на желтую молнию в верхнем ряду кнопок. На график выводится АЧХ фильтра СВЧ. Затем, не создавая нового графика, заказываем новое измерение, в окне которого заменяем имя источника данных на Lumped LPF и повторяем измерение. В результате получаем график (рис. 7.6), на котором изображены АЧХ обоих фильтров (на графике вместо Schematic 3 должно быть LPF). В полосе пропускания (частота менее 2 ГГц) они практически совпадают, в полосе ослабления кривая АЧХ фильтра СВЧ идет круче потому, что импеданс последовательной цепи фильтра СВЧ
, в окошке Data Source Name выбираем LPF, в окошке To Port Index выбираем 2, в окошке From Port Index выбираем 1, нажимаем ОК и затем на желтую молнию в верхнем ряду кнопок. На график выводится АЧХ фильтра СВЧ. Затем, не создавая нового графика, заказываем новое измерение, в окне которого заменяем имя источника данных на Lumped LPF и повторяем измерение. В результате получаем график (рис. 7.6), на котором изображены АЧХ обоих фильтров (на графике вместо Schematic 3 должно быть LPF). В полосе пропускания (частота менее 2 ГГц) они практически совпадают, в полосе ослабления кривая АЧХ фильтра СВЧ идет круче потому, что импеданс последовательной цепи фильтра СВЧ 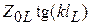 меняется при увеличении частоты быстрее, чем последовательный импеданс
меняется при увеличении частоты быстрее, чем последовательный импеданс 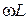 прототипного фильтра.
прототипного фильтра.



 Для оценки коэффициента отражения создадим график
Для оценки коэффициента отражения создадим график 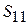 , повторив оба измерения при изменении номера в окошке To Port Index на 1. График модуля
, повторив оба измерения при изменении номера в окошке To Port Index на 1. График модуля 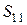 приведен на рис. 7.7. Согласование фильтра
приведен на рис. 7.7. Согласование фильтра  СВЧ несколько лучше, чем у прототипного. Это можно объяснить тем что при расчетах модели МПЛ учитывали потери в металле, в то время как при расчете прототипного фильтра потери не учитывались.
СВЧ несколько лучше, чем у прототипного. Это можно объяснить тем что при расчетах модели МПЛ учитывали потери в металле, в то время как при расчете прототипного фильтра потери не учитывались.
 7.3. Проектирование ППФ
7.3. Проектирование ППФ
Основой для проектирования ППФ на сосредоточенных элементах является ФНЧ, АЧХ и ФЧХ которого смещаются из точки 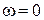 в точки
в точки 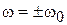 , где
, где 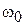 ‒ центральная частота полосы пропускания ППФ. Для ФНЧ с идеальными (без потерь) компонентами на частоте
‒ центральная частота полосы пропускания ППФ. Для ФНЧ с идеальными (без потерь) компонентами на частоте 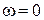 для получения единичного коэффициента передачи сопротивления параллельных элементов должны быть равными бесконечности, а для последовательных – нулю. На частоте среза
для получения единичного коэффициента передачи сопротивления параллельных элементов должны быть равными бесконечности, а для последовательных – нулю. На частоте среза 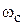 модули сопротивлений параллельных элементов должны быть равными
модули сопротивлений параллельных элементов должны быть равными 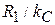 , а для последовательных ‒
, а для последовательных ‒ 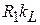 . Для обеспечения идентичности вида АЧХ и ФЧХ ППФ характеристикам «прототипного» ФНЧ необходимо, чтобы на частоте
. Для обеспечения идентичности вида АЧХ и ФЧХ ППФ характеристикам «прототипного» ФНЧ необходимо, чтобы на частоте 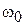 для элементов ППФ выполнялись те же требования, что для элементов ФНЧ на частоте
для элементов ППФ выполнялись те же требования, что для элементов ФНЧ на частоте 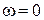 , а на частотах
, а на частотах 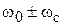 ‒ те же требования, что для элементов ФНЧ на частоте
‒ те же требования, что для элементов ФНЧ на частоте 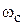 . Из первого условия следует, что параллельные элементы ППФ есть параллельные резонансные контуры с частотой резонанса
. Из первого условия следует, что параллельные элементы ППФ есть параллельные резонансные контуры с частотой резонанса 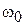 , а последовательные элементы – последовательные резонансные контуры с такой же резонансной частотой. Второе условие позволяет определить значения индуктивностей и емкостей контуров. Обозначим эквивалентные параметры параллельных резонаторов индексами p, а последовательных – индексами s, и на основании обоих условий получим выражения для определения всех реактивностей ППФ:
, а последовательные элементы – последовательные резонансные контуры с такой же резонансной частотой. Второе условие позволяет определить значения индуктивностей и емкостей контуров. Обозначим эквивалентные параметры параллельных резонаторов индексами p, а последовательных – индексами s, и на основании обоих условий получим выражения для определения всех реактивностей ППФ: 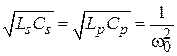 ,
, 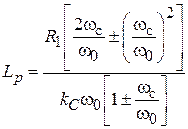 ,
, 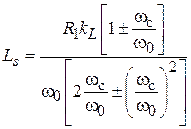 . Имея в виду, что
. Имея в виду, что 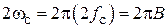 , где В – полоса пропускания ППФ, последние 2 выражения примут вид:
, где В – полоса пропускания ППФ, последние 2 выражения примут вид: 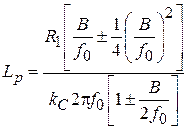 ,
, 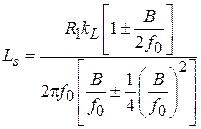 . Если
. Если 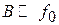 , то можно воспользоваться приближенными выражениями:
, то можно воспользоваться приближенными выражениями: 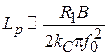 ,
, 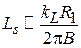 .
.
Часто последовательные контуры практически нереализуемы ввиду чрезмерно малых 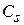 или чрезмерно больших
или чрезмерно больших 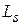 . В этом случае переходят к ППФ на основе параллельных резонаторов, связанных сосредоточенными реактивностями, чаще всего емкостями. В отечественной литературе они именуются [3] «квазиполиномиальными» фильтрами, в англоязычной – Coupled Resonators Filters [4]. Наиболее полное изложение теории и методов расчета таких фильтров можно найти в гл. 6 фундаментального руководства по синтезу фильтров [4]. Так как характеристики ППФ определяются его порядком – числом резонаторов, то при замене n последовательных резонаторов реактивностями необходимо добавить такое же число параллельных резонаторов. В [4] приведены таблицы для расчета ППФ вплоть до 10-го порядка с различными характеристиками АЧХ и ФЧХ. Однако для получения схемы прототипного ППФ для проектирования СВЧ ППФ можно воспользоваться программными средствами (AADE Filter Design and Analysis. www.aade.com., бесплатная программа и AWR Design Environment, версии начиная с 2002, в меню Tools/Manage Addins…/Filter Synthesis Wizard).
. В этом случае переходят к ППФ на основе параллельных резонаторов, связанных сосредоточенными реактивностями, чаще всего емкостями. В отечественной литературе они именуются [3] «квазиполиномиальными» фильтрами, в англоязычной – Coupled Resonators Filters [4]. Наиболее полное изложение теории и методов расчета таких фильтров можно найти в гл. 6 фундаментального руководства по синтезу фильтров [4]. Так как характеристики ППФ определяются его порядком – числом резонаторов, то при замене n последовательных резонаторов реактивностями необходимо добавить такое же число параллельных резонаторов. В [4] приведены таблицы для расчета ППФ вплоть до 10-го порядка с различными характеристиками АЧХ и ФЧХ. Однако для получения схемы прототипного ППФ для проектирования СВЧ ППФ можно воспользоваться программными средствами (AADE Filter Design and Analysis. www.aade.com., бесплатная программа и AWR Design Environment, версии начиная с 2002, в меню Tools/Manage Addins…/Filter Synthesis Wizard).
ППФ СВЧ реализуются как структуры из резонаторов в виде отрезков ЛП, замещающих параллельные и последовательные контуры в прототипном ППФ. При расчете последнего определяются значения индуктивностей и емкостей, входящих в ППФ. Замещающие резонаторы должны иметь параметры, обеспечивающие эти значения. Частотные зависимости реактивных сопротивлений резонаторов и контуров должны совпадать, по крайней мере, в области полосы пропускания ППФ и около нее. Для сосредоточенных элементов эти зависимости пропорциональны частоте, для резонаторов они нелинейно зависят от частоты. В качестве критерия совпадения характеристик примем равенство углов их наклона вблизи резонансных частот контура и резонатора. Параллельный контур замещается резонатором в виде закороченного на конце отрезка ЛП длиной 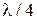 . Полное реактивное сопротивление параллельного контура
. Полное реактивное сопротивление параллельного контура 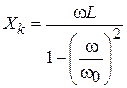 , где
, где 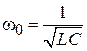 ‒ резонансная частота контура. Для резонатора
‒ резонансная частота контура. Для резонатора 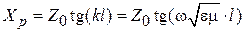 , где
, где 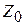 ‒ волновое сопротивление отрезка ЛП;
‒ волновое сопротивление отрезка ЛП; 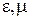 ‒ параметры среды, заполняющей ЛП;
‒ параметры среды, заполняющей ЛП; 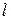 ‒ геометрическая длина отрезка. Если
‒ геометрическая длина отрезка. Если 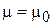 , то
, то 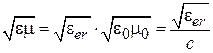 , где
, где 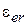 ‒ эффективная диэлектрическая проницаемость ЛП;
‒ эффективная диэлектрическая проницаемость ЛП; 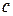 ‒ скорость света в свободном пространстве. Тогда
‒ скорость света в свободном пространстве. Тогда 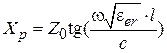 . Очевидно, что при
. Очевидно, что при 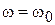 аргумент тангенса равен
аргумент тангенса равен 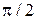 . Представим частоту
. Представим частоту 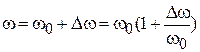 , где
, где 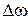 ‒ отклонение от резонансной частоты. Если полоса пропускания ППФ гораздо меньше центральной частоты,
‒ отклонение от резонансной частоты. Если полоса пропускания ППФ гораздо меньше центральной частоты, 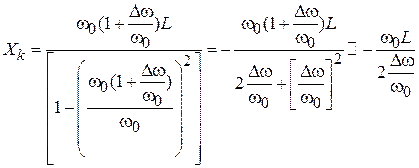 . Так как
. Так как 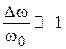 , значение сопротивления резонатора будет равно:
, значение сопротивления резонатора будет равно: 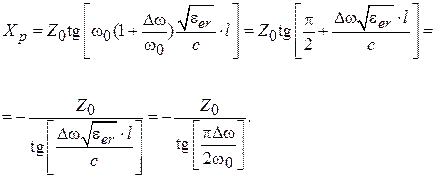
Так как тангенс малого аргумента равен самому аргументу, получим равенство: 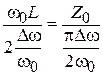 , откуда следует
, откуда следует 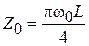 , или
, или 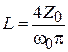 . Перейдем теперь к определению эквивалентных параметров последовательного контура и резонатора в виде полуволнового отрезка ЛП. Реактивные сопротивления контура и резонатора равны:
. Перейдем теперь к определению эквивалентных параметров последовательного контура и резонатора в виде полуволнового отрезка ЛП. Реактивные сопротивления контура и резонатора равны: 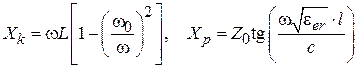 , причем аргумент тангенса на частоте
, причем аргумент тангенса на частоте 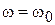 равен
равен 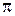 . Тогда, представляя частоту через ее приращение относительно
. Тогда, представляя частоту через ее приращение относительно 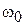 , получим равенство:
, получим равенство: 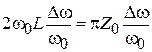 , откуда следуют выражения для эквивалентной индуктивности и волнового сопротивления отрезка ЛП:
, откуда следуют выражения для эквивалентной индуктивности и волнового сопротивления отрезка ЛП: 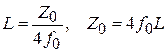 . Необходимо отметить, что диапазон возможных реализаций волнового сопротивления отрезка ЛП значительно уже, чем диапазон возможных значений индуктивностей контуров прототипного ППФ. Для микрополосковых элементов он равен, примерно 10: от 20 до 200 Ом.
. Необходимо отметить, что диапазон возможных реализаций волнового сопротивления отрезка ЛП значительно уже, чем диапазон возможных значений индуктивностей контуров прототипного ППФ. Для микрополосковых элементов он равен, примерно 10: от 20 до 200 Ом.
 Это накладывает ограничения на возможность реализации СВЧ ППФ.
Это накладывает ограничения на возможность реализации СВЧ ППФ.
 В качестве примера проектирования СВЧ ППФ рассмотрим фильтр 3-го порядка с характеристикой Баттерворта в виде П-структуры с характеристическим сопротивлением
В качестве примера проектирования СВЧ ППФ рассмотрим фильтр 3-го порядка с характеристикой Баттерворта в виде П-структуры с характеристическим сопротивлением 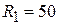 Ом, с центральной частотой
Ом, с центральной частотой 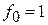 ГГц и полосой пропускания
ГГц и полосой пропускания 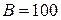 МГц. Расчет полиномиального фильтра дает следующие значения емкостей и индуктивностей:
МГц. Расчет полиномиального фильтра дает следующие значения емкостей и индуктивностей: 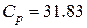 пФ,
пФ, 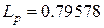 нГн,
нГн, 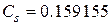 пФ,
пФ, 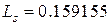 нГн. Последние 3 значения трудно реализуемы. Поэтому рассчитаем фильтр на связанных резонаторах с помощью программы Filter Design. Откроем программу и в меню Design выберем Coupled Resonator/Butterwort. В открывшемся окне выберем CF=1000.0 М, BW=100.0 M, Order=3 и нажмем на кнопку ENTER. В новом окне выберем Lossless (без потерь). В качестве минимального значения индуктивности параллельных контуров предлагается 1.598 нГн. Выберем большее значение – 10 нГн (при этом возрастет R фильтра, но его можно будет позже трансформировать в 50 Ом). Нажав ENTER, переходим в следующее окно, где (по умолчанию) предлагается значение R = 623 Ом на входе и на выходе фильтра. Заменим его на 50 и нажмем на ENTER. В открывшемся окне назовем фильтр BPF1000, после чего появится схема спроектированного ППФ (рис. 7.8).
нГн. Последние 3 значения трудно реализуемы. Поэтому рассчитаем фильтр на связанных резонаторах с помощью программы Filter Design. Откроем программу и в меню Design выберем Coupled Resonator/Butterwort. В открывшемся окне выберем CF=1000.0 М, BW=100.0 M, Order=3 и нажмем на кнопку ENTER. В новом окне выберем Lossless (без потерь). В качестве минимального значения индуктивности параллельных контуров предлагается 1.598 нГн. Выберем большее значение – 10 нГн (при этом возрастет R фильтра, но его можно будет позже трансформировать в 50 Ом). Нажав ENTER, переходим в следующее окно, где (по умолчанию) предлагается значение R = 623 Ом на входе и на выходе фильтра. Заменим его на 50 и нажмем на ENTER. В открывшемся окне назовем фильтр BPF1000, после чего появится схема спроектированного ППФ (рис. 7.8).
Емкости на входе и на выходе фильтра (по 0.93818 пФ) трансформируют сопротивление 623 Ом в 50 Ом, индуктивности во всех трех контурах равны 10 нГн, емкости первого и третьего контуров равны 1.43278 пФ, емкость второго контура – 2.18982 пФ, емкости связи – по 0.18114 пФ. Для вывода АЧХ фильтра выберем в меню ANALIZE/Power Effective Gain, после чего откроется окно для задания параметров анализа АЧХ. Выберем минимальную частоту 700 МГц, максимальную – 1300 МГц, максимальное ослабление ‒60 дБ, нажмем ENTER и выведем график АЧХ, показанный на рис. 7.9.

 Характеристика несимметрична, что характерно для фильтров на связанных резонаторах, и ввиду отсутствия потерь ослабление в полосе пропускания очень близко к нулю. Определим резонансные частоты для всех трех контуров фильтра:
Характеристика несимметрична, что характерно для фильтров на связанных резонаторах, и ввиду отсутствия потерь ослабление в полосе пропускания очень близко к нулю. Определим резонансные частоты для всех трех контуров фильтра: 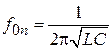 . Получим следующие значения:
. Получим следующие значения: 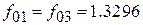 ГГц,
ГГц, 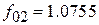 ГГц (номера в индексах определяются положением контура слева направо). Отличие их от центральной частоты всего ППФ объясняется тем, что к емкостям контуров добавляются емкости связи, а для первого и третьего контуров – трансформированные значения согласующих емкостей на входе и выходе фильтра. Перейдем теперь к замене параллельных контуров резонаторами в виде короткозамкнутых четвертьволновых отрезков МПЛ. Каждый резонатор должен иметь длину, равную четверти длины волны, и эквивалентную индуктивность, равную 10 нГн, на своей резонансной частоте. Ранее было получено выражение для эквивалентной индуктивности четвертьволнового отрезка ЛП с волновым сопротивлением
ГГц (номера в индексах определяются положением контура слева направо). Отличие их от центральной частоты всего ППФ объясняется тем, что к емкостям контуров добавляются емкости связи, а для первого и третьего контуров – трансформированные значения согласующих емкостей на входе и выходе фильтра. Перейдем теперь к замене параллельных контуров резонаторами в виде короткозамкнутых четвертьволновых отрезков МПЛ. Каждый резонатор должен иметь длину, равную четверти длины волны, и эквивалентную индуктивность, равную 10 нГн, на своей резонансной частоте. Ранее было получено выражение для эквивалентной индуктивности четвертьволнового отрезка ЛП с волновым сопротивлением 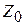 :
: 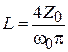 . Тогда значение волнового сопротивления определится как
. Тогда значение волнового сопротивления определится как 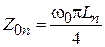 .
.
 После расчета получаем:
После расчета получаем: 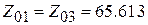 Ом,
Ом, 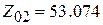 Ом. Геометрические размеры отрезков МПЛ определим с помощью TXLine, полагая, что подложка такая же, как и в случае СВЧ ФНЧ: Н = 4 мм,
Ом. Геометрические размеры отрезков МПЛ определим с помощью TXLine, полагая, что подложка такая же, как и в случае СВЧ ФНЧ: Н = 4 мм, 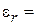 2.16. Электрическая длина отрезка всегда равна 90°, частоты и волновые сопротивления – в соответствии с расчетом. Получаем:
2.16. Электрическая длина отрезка всегда равна 90°, частоты и волновые сопротивления – в соответствии с расчетом. Получаем: 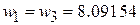 мм, длина
мм, длина 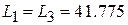 мм,
мм, 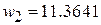 ,
, 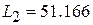 мм. В качестве емкостей связи и согласующих емкостей используем сосредоточенные элементы (при необходимости реализации ППФ только на МПЛ можно использовать встречно-штыревые емкости, которые находятся в Elements/Circuit Elements/Microstrip/Component/MICAP).
мм. В качестве емкостей связи и согласующих емкостей используем сосредоточенные элементы (при необходимости реализации ППФ только на МПЛ можно использовать встречно-штыревые емкости, которые находятся в Elements/Circuit Elements/Microstrip/Component/MICAP).


 Для моделирования фильтра в MWO откроем проект BPF, в Options/Project Options/Frequency закажем интервал частот от 0.7 до 1.3 ГГц с шагом 0.01 ГГц, в Project/Schematic/New Schematic закажем схему, назвав ее BPF, и построим схему, показанную на рис. 7.10. Затем закажем новую схему, назвав ее Lumped BPF, и построим схему (рис. 7.11), повторяющую схему рис. 7.8.
Для моделирования фильтра в MWO откроем проект BPF, в Options/Project Options/Frequency закажем интервал частот от 0.7 до 1.3 ГГц с шагом 0.01 ГГц, в Project/Schematic/New Schematic закажем схему, назвав ее BPF, и построим схему, показанную на рис. 7.10. Затем закажем новую схему, назвав ее Lumped BPF, и построим схему (рис. 7.11), повторяющую схему рис. 7.8.


 Затем закажем график в прямоугольных координатах и назовем его S21. Далее закажем измерение модуля S21 в децибелах, выбрав в качестве источника данных Lumped BPF, затем повторим измерение, выбрав BPF. В результате получим
Затем закажем график в прямоугольных координатах и назовем его S21. Далее закажем измерение модуля S21 в децибелах, выбрав в качестве источника данных Lumped BPF, затем повторим измерение, выбрав BPF. В результате получим  графики (рис. 7.12). Центральная частота BPF немного ниже 1 ГГц. Для коррекции центральной частоты BPF вверх необходимо откорректировать длину резонаторов. С помощью маркеров определим частоты обоих фильтров на уровне ‒20 дБ, найдем среднюю частоту полосы пропускания
графики (рис. 7.12). Центральная частота BPF немного ниже 1 ГГц. Для коррекции центральной частоты BPF вверх необходимо откорректировать длину резонаторов. С помощью маркеров определим частоты обоих фильтров на уровне ‒20 дБ, найдем среднюю частоту полосы пропускания 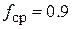 ГГц, найдем отношение
ГГц, найдем отношение


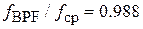 умножим на это значение длины отрезков МПЛ и получим длину крайних отрезков 41.28 мм, центрального – 50.55 мм. Изменим на схеме BPF эти длины и после расчета получим график (рис. 7.13). Центральные частоты обоих фильтров теперь совпадают, полоса пропускания BPF чуть больше, чем у Lumped BPF. Теперь найдем модуль
умножим на это значение длины отрезков МПЛ и получим длину крайних отрезков 41.28 мм, центрального – 50.55 мм. Изменим на схеме BPF эти длины и после расчета получим график (рис. 7.13). Центральные частоты обоих фильтров теперь совпадают, полоса пропускания BPF чуть больше, чем у Lumped BPF. Теперь найдем модуль 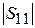 . Закажем новый график с названием S11, затем измерение модуля (Mag) S11 в децибелах и, повторив, как в первом измерении, все действия, получим график (рис. 7.14). Очевидно достаточно хорошее совпадение характеристик прототипного и СВЧ ППФ.
. Закажем новый график с названием S11, затем измерение модуля (Mag) S11 в децибелах и, повторив, как в первом измерении, все действия, получим график (рис. 7.14). Очевидно достаточно хорошее совпадение характеристик прототипного и СВЧ ППФ.
Список литературы
1. Разевиг В. Д., Потапов Ю. В., Курушин А. А. Проектирование СВЧ устройств с помощью «Microwave Office» / Под ред. В. Д. Разевига. М.: СОЛОН-Пресс, 2003.
2. Аршинов С. С., Персон С. В., Эйленкриг А. И. Инженерный расчет контуров генераторов УКВ и КВ (отрезки длинных линий и объемные резонаторы). М.: Сов. радио, 1952.
3. Ханзел Г. Е. Справочник по расчету фильтров / Пер. с англ.; под ред. А. Е. Знаменского. М.: Сов. радио, 1974.
4. Zverev A. I. Handbook of Filter Synthesis. N. Y.: John Wiley, 1967.
5. Зааль Р. Справочник по расчету фильтров / Пер. с нем. М.: Радио и связь, 1983.
Дата добавления: 2017-11-04; просмотров: 878;
