Точечная оценка параметров

Процедура точечной оценки исходит из задач математической статистики, определяющим понятием которой является параметр. Параметр (отмеривающий) – величина, значения которой служат для различения элементов некоторого множества между собой. Например, (х - а)² + (у – b)²=1 определяет множество всех окружностей радиуса R=1, где а=3; b=4; выделяют из этого множества вполне определенную окружность с центрами (3,4).

В качестве точечной оценки какого-либо параметра q распределения вероятностей следует выбирать такую функцию q (t₁, … t_n) от результатов наблюдений t₁, … t_n, которая в некотором определенном смысле близка к истинному значению параметра. Принимая какую-либо меру близости оценки к параметру, можно сравнивать различные оценки.

Из приведенного определения следует, что оценка зависит от результатов испытаний и является случайной величиной. Любая оценка, для того, чтобы «быть близкой» к истинному значению параметра должна обладать рядом свойств. Критериями качества точечных оценок служат такие характеристики как состоятельность, несмещенность, эффективность.

Оценка параметра q (t₁, … t_n) является состоятельной, если при увеличении числа испытаний до 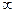оценка по вероятности сходится к оцениваемому параметру q:

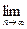
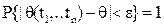, e>0.

Оценка параметра q (t₁, … t_n) называется несмещенной, если ее математическое ожидание (М) равно оцениваемому параметру q:

Мq (t₁, … t_n) = q.

Несмещенность оценки означает отсутствие у нее систематической ошибки. Эффективной называют оценку, которая (при заданном объеме испытаний) имеет наименьшую дисперсию:

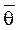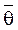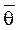D (t₁, … t_n) = min ( D ₁,… D _k).

Перечисленные свойства определяют требования к качеству оценки. Однако не дают ответа на вопрос: «как искать эту оценку?» Наиболее распространенными общими методами получения точечных оценок являются методы моментов, максимального правдоподобия и наименьших квадратов.

Суть метода моментов заключается в приравнивании определенного числа выборочных моментов (полученных при обработке статистического материала), соответствующим моментам исходного распределения, которое является функцией от неизвестных параметров, и решения полученных уравнений относительно этих параметров.

При сравнении методов наибольшее предпочтение при получении точечных оценок отдается методам максимального правдоподобия и методам наименьших квадратов, обладающих более лучшими асимптотическими свойствами показателей состоятельности оценки. Поэтому уделим больше внимания методам максимального правдоподобия и наименьших квадратов.

Метод максимального правдоподобия – метод нахождения точечных оценок неизвестных параметров распределения, согласно которому в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдения «наиболее вероятны».

Обычно предполагается, что результаты наблюдений t₁, …. t_n являются взаимно независимыми случайными величинами с одним и тем же распределением вероятностей, зависящих от одного неизвестного параметра – множество допустимых значений q. Для придания точного смысла принципу «наибольшей вероятности» поступают следующим образом. Вводят функцию L от переменных t₁, … t_n и q_1.

,

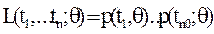где p (t_k, q) в случае непрерывного распределения, интерпретируется как плотность вероятности случайной величины t, а в дискретном случае – как вероятность того, что случайная величина t примет значение t _k.

Смысл вводимой функции состоит в отражении вероятности совместного появления события, заключающегося в том, что t в n опытах примет значения t₁, … t_n. Так как это событие произошло (раз мы наблюдали именно эти значения), вероятность такого события должна быть наибольшей. Наша задача найти такое значение q, при котором L(·) имеет экстремум.

Функцию L (t₁, … t_n, q) от случайных величин t₁, … t_n, рассматриваемую как функцию q, называют функцией правдоподобия, а оценкой максимального правдоподобия называют такое значение: 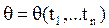, при котором функция правдоподобия достигает наибольшего возможного значения.

На практике для удобства вычислений обычно используется функция ln L, так как точка максимума для ln L и L одна и та же. Для нахождения оценок максимального правдоподобия следует решить уравнение правдоподобия:

.

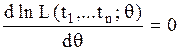Приведенное описание метода максимального правдоподобия может быть обобщено и на случай нескольких неизвестных параметров.

Метод наименьших квадратов. Идея метода наименьших квадратов заключается в следующем. Пусть имеются результаты n независимых опытов, оформленные в виде простой статистической таблицы 3.2.

Таблица 3.2

Точки (х_i, у_i) нанесены на график (рисунок 3.6)

Рисунок 3.6

Из теоретических или иных соображений выбран принципиальный вид зависимости y = φ(х). Функция y = φ(х) содержит ряд числовых параметров a,b, c,… . Требуется так выбрать эти параметры, чтобы кривая y = φ(х) в некотором известном смысле наилучшим образом отображала зависимость, полученную в опыте. С точки зрения метода наименьших квадратов «наилучшее» согласование кривой y = φ(х) и экспериментальных точек сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей (теоретической) кривой обращалась в минимум. Рассмотренный метод имеет веское и теоретическое обоснование. Предположим, что истинная зависимость у от х в точности выражается формулой y = φ(х). Экспериментально намеренные значения отклоняются от истинных значений вследствие неизбежных ошибок измерений. Допустим, что ошибки измерения подчиняются нормальному закону. Предположим, что точность во всех измерениях одинакова: .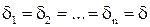

Тогда нормальный закон, по которому распределена величина у_i, можно записать в виде:

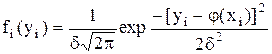(43)

В результате ряда измерений произошло следующее событие: случайные величины (У₁, У₂, …, У_n) приняли совокупность значений (у₁, у_2,…у₃). Поставим задачу: так подобрать математические ожидания 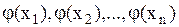, чтобы вероятность этого события была максимальна. Найдем вероятность того, что система случайных величин У₁,…,У_n примет совокупность значений, лежащих в пределах (у₁,у_i + dy_i); i =1,..,n.

Так как опыты независимы, эта вероятность равна произведению элементов вероятностей для всех значений i.

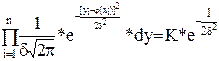
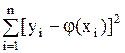(44)

где К – некоторый коэффициент, независящий от 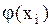. Требуется так подобрать 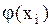, чтобы выражение (44) обращалось в максимум.

Величина 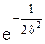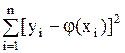, всегда меньше 1 и она имеет max значение, когда показатель по абсолютной величине обращается в min:

.

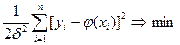Отбрасывая постоянный множитель 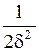, получим требование метода наименьших квадратов: для того, чтобы вероятность данной совокупности наблюденных значений у₁ от 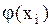была максимальной, необходимо чтобы

.

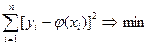Таким образом, метод наименьших квадратов основывается на предположении о нормальном законе распределения ошибок измерения и требования максимальной вероятности данной совокупности значений.

На практике для того, чтобы воспользоваться данным методом поступают следующим образом:

- записывают функцию y как функцию аргумента и параметров

y =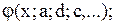

- определяют условие минимума по методу наименьших квадратов:

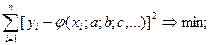
- находят min этого выражения путем дифференцирования по параметрам и приравнивания левой части к нулю:

,

.

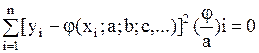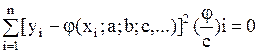Эта система содержит столько уравнений, сколько неизвестных параметров a,d,c… . Представляя конкретное выражение вместо 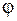, эту систему можно разрешить относительно a,d,c…

Таким образом, методы максимального правдоподобия и наименьших квадратов, исходя из принципа наибольшей вероятности наблюденных значений, позволяют получать точечные оценки неизвестных параметров законов распределения.

ЗАКЛЮЧЕНИЕ

Таким образом, на нашем занятии мы рассмотрели виды структурных схем расчета надежности, методы расчета показателей надежности не резервированных систем, уяснили порядок нахождения показателей надёжности этими методами.