Примеры решения задач
ПРИМЕР 2.42. Однородная струна длины 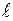 совершает малые поперечные колебания. Поставить задача об определении отклонений
совершает малые поперечные колебания. Поставить задача об определении отклонений 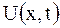 точек струны от прямолинейного положения покоя, если в момент
точек струны от прямолинейного положения покоя, если в момент 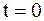 струна имела форму
струна имела форму 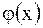 (
( 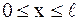 ) и скорость каждой ее точки задается функцией
) и скорость каждой ее точки задается функцией  . Рассмотреть случаи:
. Рассмотреть случаи:
а) концы струны закреплены;
б) концы струны свободны;
в) к концам струны 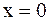 и
и 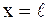 , начиная с момента
, начиная с момента 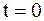 , приложены поперечные силы
, приложены поперечные силы 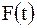 и
и 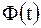 соответственно;
соответственно;
г) концы струны закреплены упруго, т.е. каждый из концов испытывает сопротивление, пропорциональное отклонению конца.
Решение. Как известно, отклонения 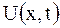 точек струны от положения равновесия удовлетворяют в отсутствии действующей внешней силы уравнению свободных колебаний (2.70)
точек струны от положения равновесия удовлетворяют в отсутствии действующей внешней силы уравнению свободных колебаний (2.70)
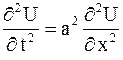 .
.
Здесь 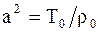 ,
, 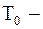 натяжение, линейная плотность
натяжение, линейная плотность  , т.к. струна однородная.
, т.к. струна однородная.
Начальные условия имеют вид:
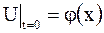 ,
, 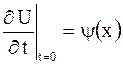 ,
, 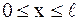 .
.
Займемся выводом граничных условий.
Случай а). Так как концы струны закреплены, то их отклонения 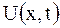 в точках
в точках 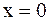 и
и 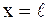 должны быть равными нулю при любом
должны быть равными нулю при любом 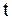 , т.е.
, т.е.
 ,
, 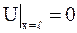 ,
, 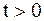 .
.
Итак, физическая задача о колебаниях закрепленной на концах струны свелась к следующей математической задаче: найти функцию 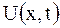 , определенную при
, определенную при  и
и 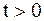 , являющуюся решением уравнения
, являющуюся решением уравнения
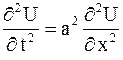
и удовлетворяющую граничным условиям
 ,
, 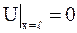
и начальным условиям
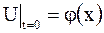 ,
, 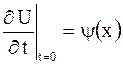 .
.
Случай б). Если концы струны свободны, то внешние силы, приложенные к ним, равны нулю. И, следовательно, равна нулю сила натяжения 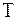 , которая согласно закону Гука, пропорциональна удлинению:
, которая согласно закону Гука, пропорциональна удлинению: 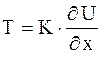 , где коэффициент
, где коэффициент 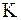 включает модуль упругости материала. Поэтому
включает модуль упругости материала. Поэтому
 ,
, 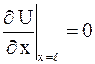 ,
, 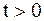 ,
,
Задача формулируется следующим образом: найти решение уравнения
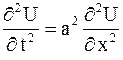 ,
,  ,
, 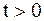 ,
,
удовлетворяющее граничным условиям
 ,
, 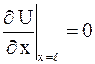
и начальным условиям
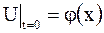 ,
, 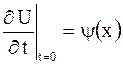 .
.
Случай в). Рассмотрим граничные элементы 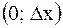 и
и 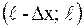 . Запишем второй закон Ньютона для правого элемента
. Запишем второй закон Ньютона для правого элемента 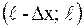 , на который действует сила
, на который действует сила 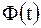 и сила натяжения
и сила натяжения 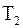
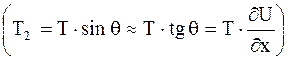 :
:

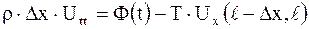
Переходя к пределу при 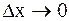 , получим
, получим
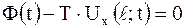 , откуда
, откуда  .
.
Аналогично получим условия для левого конца:
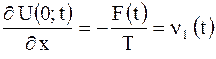 .
.
Таким образом, задача ставится так: найти в области  ,
, 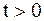 , решение уравнения
, решение уравнения
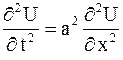 ,
,
удовлетворяющее граничным условиям 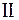 рода
рода
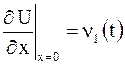 ,
, 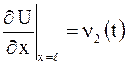
и начальным условиям
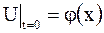 ,
, 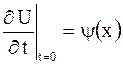 .
.
Случай г). При упругом закреплении концов каждый конец испытывает сопротивление, пропорциональное отклонению конца, т.е.
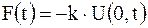 ,
, 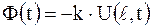 ,
,
где 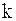 - коэффициент жесткости упругого крепления концов струны. Тогда из граничных условий в случае в) получим
- коэффициент жесткости упругого крепления концов струны. Тогда из граничных условий в случае в) получим
 ,
, 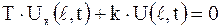 ,
,
иначе 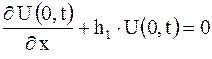 ,
, 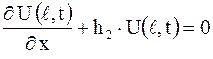 .
.
Математическая формулировка задачи: найти решение уравнения
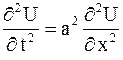 ,
,
удовлетворяющее граничным условиям III рода
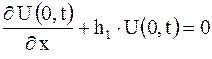 ,
, 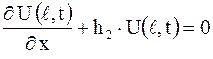 ,
, 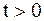
и начальным условиям
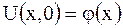 ,
, 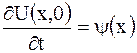 ,
, 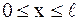 .
.
Дата добавления: 2017-10-09; просмотров: 798;
