Розподіли та з ступенями вільності

ДЕЯКІ РОЗПОДІЛИ, ЯКІ ЗАСТОСОВУЮТЬ В МАТЕМАТИЧНІЙ СТАТИСТИЦІ

В цій лекції розглядається декілька законів розподілу, які складають необхідний апарат для побудови статистичних критеріїв та оцінок, що застосовуються, перш за все, в математичній статистиці.

Гамма-розподіл

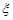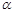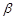Означення 23.1. Невід’ємна випадкова величина має гамма-розподіл з параметрами та , якщо її щільність розподілу дорівнює

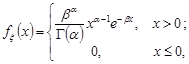
де 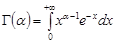– гамма-функція.

Окремим випадком гамма-розподілу є показниковий розподіл, для якого 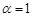, 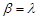. Дійсно, при таких параметрах

, .

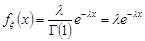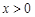Знайдемо початкові моменти гамма-розподілу.

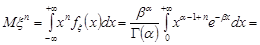
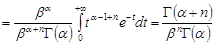При 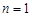маємо математичне сподівання випадкової величини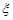

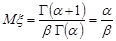Другий початковий момент буде таким:

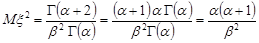Отже, дисперсія гамма-розподілу дорівнює

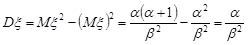Приклад 23.1. Скласти композицію двох випадкових величин 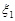та 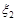, розподілені за гамма-розподілом із параметрами 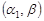та .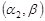

Розв’язання. За формулою (21.3)

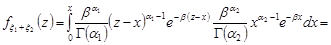
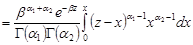В останньому інтегралі зробимо заміну 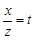, тоді

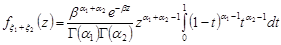Оскільки

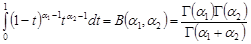, то при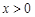

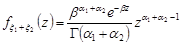тобто також гамма-розподіл з параметрами .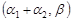

Розподіли та з ступенями вільності

(розподіл Пірсона)

Розглянемо випадковий вектор 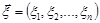, компоненти якого є незалежними, нормально розподіленими випадковими величинами з параметрами .

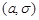Означення 23.2. Закон розподілу випадкової величини 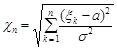називається розподілом “хі з 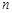ступенями вільності”.

Знайдемо функцію та щільність розподілу цієї випадкової величини. Щільність розподілу 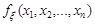випадкових величин 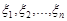має вигляд

.

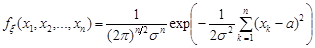Функція розподілу випадкової величини 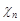за означенням дорівнює

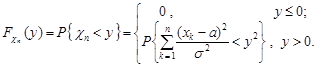
Знайдемо вираз 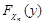для :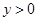

,

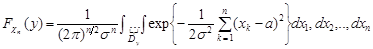де .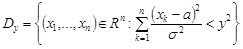

Введемо заміну 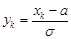. Тоді

.

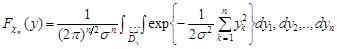Застосуємо узагальнені сферичні координати:

;

;

...........

.

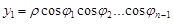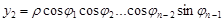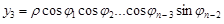
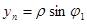Тоді 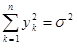. Якобіан перетворення дорівнює

.

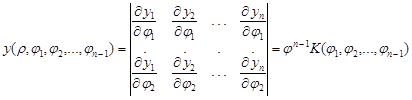Область, по якій треба інтегрувати, симетрична відносно початку координат, а підінтегральна функція парна відносно кожної змінної. Отже, достатньо обчислити цей інтеграл тільки по тій частині області, де 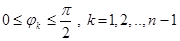, а результат помножити на відповідне число, яке навіть нема необхідності знати, тобто

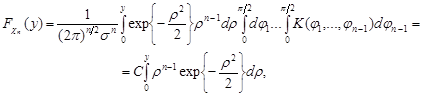де 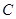– деяка константа. Обчислимо її, враховуючи, що

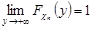. Маємо 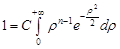. Отже,

.

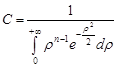Введемо заміну змінних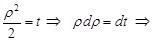

.

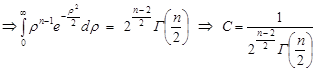Остаточно функція розподілу має вигляд

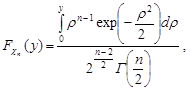при .

Запишемо щільність розподілу випадкової величини :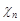

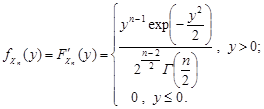
Розглянемо ще одну випадкову величину вигляду 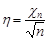і знайдемо її закон розподілу.

.

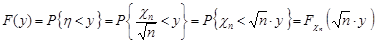Отже,

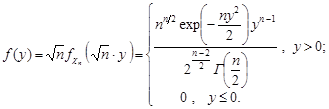
Означення 23.3. Закон розподілу випадкової величини 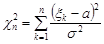називається розподілом “хі-квадрат з 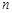ступенями вільності” ( або розподілом Пірсона).

Із результатів лекції 20 випливає, що щільності розподілів 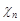та 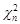пов’язані співвідношенням , .

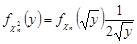Таким чином,

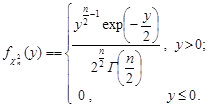
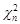Із вигляду щільності розподілу видно, що розподіл є окремим випадком гамма-розподілу з параметрами 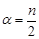та 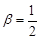. Отже, числові характеристики розподілу 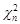знайдемо з числових характеристик гамма-розподілу:

, .

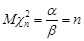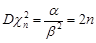Розподіл Стьюдента

Означення 23.3.Закон розподілу випадкової величини 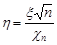, де величина 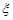має нормальний розподіл 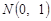, величина 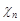має розподіл “хі з 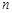ступенями вільності” та обидві вони незалежні називається розподілом Стьюдентаз 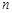ступенями вільності” (або 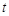-розподілом).

Для знаходження щільності розподілу Стьюдента використаємо формулу (21.2) та умову незалежності випадкових величин:

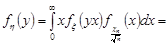
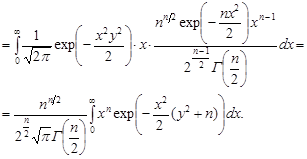
Зробимо заміну змінних

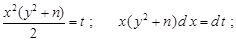
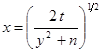Тоді щільність розподілу закону Стьюдента набуває вигляду

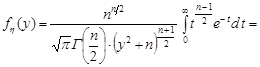
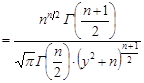при .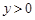

При 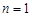розподіл Стьюдента стає розподілом Коші

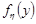
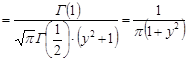Оскільки щільність розподілу Стьюдента є парна функція, то всі його початкові моменти непарного порядку дорівнюють нулю, отже, 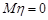. Знайдемо значення для моментів парного порядку.

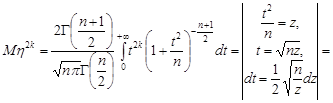
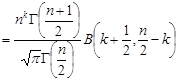де 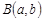– бета-функція, яка визначається так: 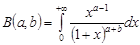, , 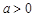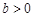. Як відомо, бета-функція зв’язана з гамма-функцією співвідношенням 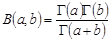, отже, парні моменти можна записати так:

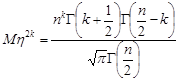Покладемо в цій формулі 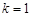, отримаємо

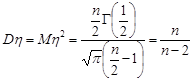При 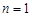розподіл Стьюдента стає розподілом Коші. А при достатньо великих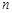 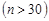, розподіл Стьюдента набуває значень близьких до нормального розподілу .

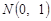<== предыдущая лекция	\|	следующая лекция ==>
Зв’язок між характеристичною функцією цілочислових дискретних випадкових величин та генератрисою	\|	Види збіжностей послідовності випадкових величин

Дата добавления: 2017-02-20; просмотров: 402;