Задания для самостоятельного решения
I уровень
1.1. Найдите производную функции:
1) 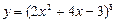 ; 2)
; 2) 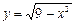 ;
;
3) 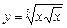 ; 4)
; 4) 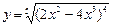 ;
;
5) 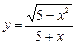 ; 6)
; 6) 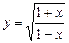 ;
;
7) 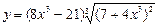 ; 8)
; 8) 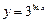 ;
;
9) 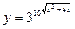 ; 10)
; 10) 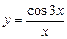 ;
;
11) 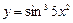 ; 12)
; 12) 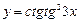 ;
;
13) 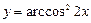 ; 14)
; 14) 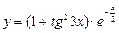 ;
;
15) 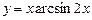 ; 16)
; 16) 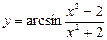 ;
;
17) 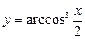 ; 18)
; 18) 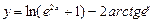 .
.
1.2. Найдите производную функции при данном значении аргумента:
1) 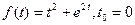 ;
;
2) 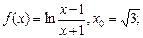
3) 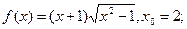
4) 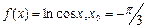
5) 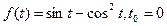
6) 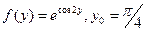
7) 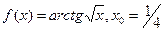
8) 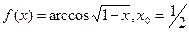
1.3. Решите неравенство 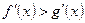 , где
, где 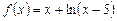 и
и 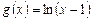 .
.
II уровень
2.1. Вычислите 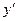 , если
, если
1) 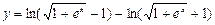 ; 2)
; 2) 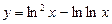 ;
;
3) 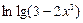 ; 4)
; 4) 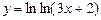 ;
;
5) 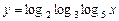 ; 6)
; 6) 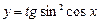 ;
;
7) 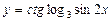 ;
;
8) 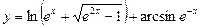 ;9)
;9) 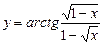 ;
;
10) 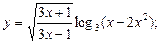 11)
11) 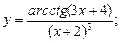
12) 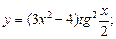 13)
13) 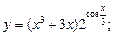
14) 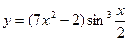 .
.
2.2. Вычислите производную функции при заданном значении аргумента:
1) 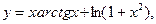
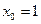 ;
;
2) 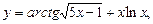
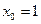 ;
;
3) 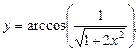
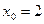 ;
;
4) 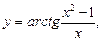
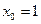 ;
;
5) 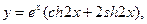
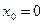 ;
;
6) 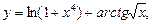
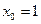 ;
;
7) 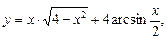
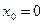 ;
;
8) 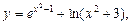
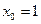 .
.
2.3. Вычислите значение производной 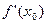 , предварительно упростив выражение:
, предварительно упростив выражение:
1) 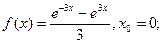 2)
2) 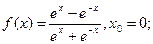
3) 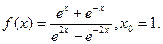
2.4. Вычислите производную функции, предварительно упростив выражение:
1) 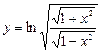 ; 2)
; 2)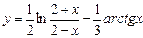 ;
;
3) 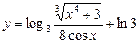 ;
;
4) 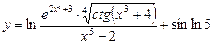 .
.
2.4. Известно, что 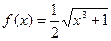 и
и 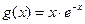 . Найдите значение выражения
. Найдите значение выражения 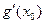 где
где 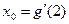 .
.
2.5. Найдите производную функции 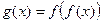 если
если 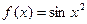 .
.
2.6. Найдите производную функции 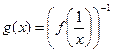 если
если 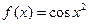 .
.
2.7. Докажите тождество:
а) 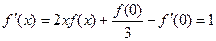 если
если 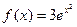 ;
;
б) 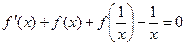 если
если 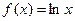 .
.
Ш уровень
3.1. Найдите производную функции:
1) 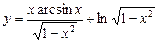 ; 2)
; 2) 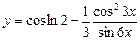 ;
;
3) 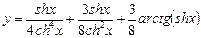 ;
;
4) 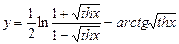 .
.
3.2. Найти производную функции, предварительно преобразовав выражение по тригонометрическим формулам:
1) 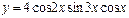 ; 2)
; 2) 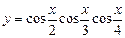 ;
;
3) 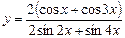 ;
;
4) 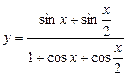
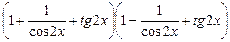 ;
;
5) 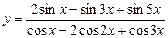 .
.
6) 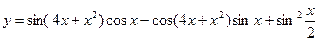 .
.
3.3. Дана функция 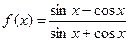 Определите, чему равно значение выражения
Определите, чему равно значение выражения 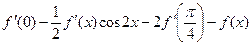 .
.
3.4. Даны функции 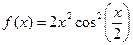 и
и 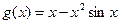 . Найдите количество значений
. Найдите количество значений 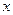 на отрезке
на отрезке 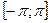 , для которых выполняется равенство
, для которых выполняется равенство 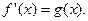 .
.
Уравнение касательной и нормали.
Дата добавления: 2017-09-19; просмотров: 295;
