Задания для самостоятельного решения
I уровень
1.1. Последовательность 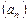 задана формулой
задана формулой 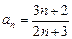 . Найдите
. Найдите 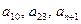 .
.
1.2. Запишите первые пять членов последовательности:
1) 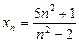 ; 2)
; 2) 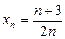 ;
;
3) 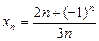 ; 4)
; 4) 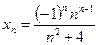 ;
;
1.3. Последовательность задана формулой 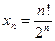 . Найдите
. Найдите 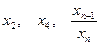 .
.
1.4. Найдите первые пять членов последовательности ( 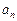 ), заданной реккурентно:
), заданной реккурентно:
1) 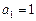 и
и 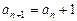 ;
;
2) 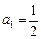 и
и 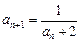 ;
;
3) 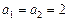 и
и 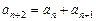 .
.
1.5. Докажите, что последовательность, заданная формулой общего члена, является возрастающей:
1) 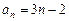 ; 2)
; 2) 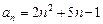 .
.
1.6. Докажите, что последовательность, заданная формулой общего члена, является убывающей:
1) 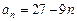 ; 2)
; 2) 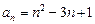 ; 3)
; 3) 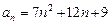 .
.
1.7. Изобразите первые семь членов последовательности ( 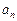 ) на числовой оси, если
) на числовой оси, если
1) 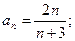 2)
2) 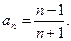
1.8. Известно, что членом последовательности являются числа, каждое из которых, начиная с 0, на 2 единицы больше предыдущего. Запишите первые 5 членов этой последовательности.
II уровень
2.1. Запишите первые шесть членов последователь- ности (xn):
1) 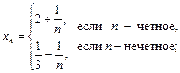
2) 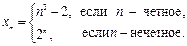
2.2. Запишите первые шесть членов последовательности:
1) чётных, натуральных чисел, кратных числу 3.
2) натуральных чисел, которые при делении на 7 дают остаток 5.
3) натуральных чисел, кратных числам 3 и 4.
Укажите формулу n-го члена последовательности.
2.3. Определите, содержится ли среди членов числовой последовательности 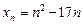 число:
число:
1) 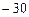 ; 2)
; 2) 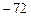 ; 3)
; 3) 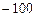 .
.
2.4. Исследуйте последовательность на ограниченность:
1) 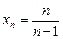 ; 2)
; 2) 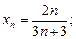 3)
3) 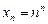 ;
;
4) 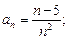 5)
5) 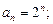 6)
6) 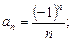
7) 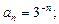 8)
8) 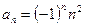 .
.
2.5. Изобразите графически ( в системе координат 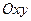 10 членов последовательности (
10 членов последовательности ( 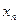 ), если
), если
1) 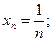 2)
2) 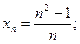
3) 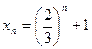 ; 4)
; 4) 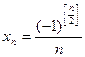 .
.
III уровень
3.1. Найдите первые девять членов последовательности Фибоначчи, заданной реккурентно:
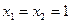 и
и 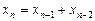 ,
, 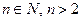 .
.
3.2. Запишите первые шесть членов последовательности приближенных значений 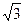 с точностью до
с точностью до 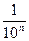 (по недостатку).
(по недостатку).
3.3. Определите, для каких членов последовательности 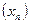 , заданной формулой
, заданной формулой 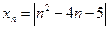 не выполняется условие
не выполняется условие 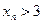 .
.
3.4. Последовательность 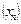 задана формулой
задана формулой 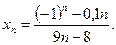 Определите сколько членов этой последовательности принадлежит промежутку
Определите сколько членов этой последовательности принадлежит промежутку 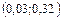 .
.
3.5. Последовательность 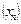 задана формулой
задана формулой 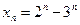 . Установите, верно ли равенство
. Установите, верно ли равенство 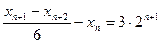 .
.
Дата добавления: 2017-09-19; просмотров: 416;
