Рекуррентная формула

При суммировании ряда необходимо решить следующие задачи:

a) свести вычисления к простейшим арифметическим операциям;

b) уменьшить число этих операций и время расчета;

c) уменьшить погрешность округления.

Рассмотрим вычисление функции sin x. Разложение этой функции в ряд Тейлора имеет следующий вид

.

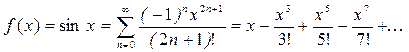Область сходимости ряда определяется неравенством 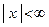, то есть ряд сходится при любом значении x.

Величина n! называется “n-факториал” и вычисляется по формуле:

n! = 1 × 2 × 3 × … × (n – 1) × n = (n – 1)! × n или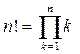

Принято считать, что 0! = 1.

Суммирование ряда последовательным вычислением слагаемых и добавлением их к сумме, как на приведенной выше блок-схеме, сводит вычисления к простейшим арифметическим операциям, то есть первая задача при этом решается. Что касается второй задачи – уменьшения количества этих операций, – то многократное перемножение чисел в числителе (степени x) и в знаменателе (n!) вряд ли можно считать рациональным. При этом (третья задача) погрешность вычислений возрастает с увеличением номера члена ряда – слишком велики становятся и числитель, и знаменатель.

Задачи сокращения количества операций и уменьшения погрешности вычислений решает рекуррентная формула, позволяющая вычислить значение очередного члена ряда, используя уже найденное значение предыдущего. Рекуррентная формула имеет вид:

a_n+1 = a_n × T_n, где T_n – коэффициент рекурсии.

В нашем примере произвольный член ряда определяется формулой:

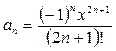, где n = 0, 1, 2, ...

Номер начального члена ряда n = 0, его значение a₀ = x.

Для расчета коэффициента рекурсии

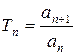
определим значение следующего (n+1)-го члена ряда.

В формулу общего члена ряда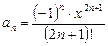

вместо n подставим (n+1), получим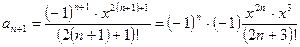

Вычисляя коэффициент рекурсии, сокращаем дробь:

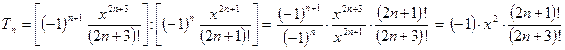
Чтобы сократить факториалы, рассмотрим числитель и знаменатель отдельно:

(2n + 1)! = 1 × 2 × 3 × … × (2n + 1)

(2n + 3)! = 1 × 2 × 3 × … × (2n + 1) × (2n + 2) × (2n + 3)

Окончательная формула коэффициента рекурсии

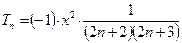
Отсюда получаем рекуррентную формулу для вычисления членов ряда

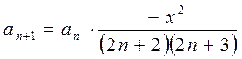
Проверка полученной формулы убережет Вас от ошибок в алгоритме и, возможно, сэкономит усилия при отладке программы.

Подставив n = 0 в формулу общего члена ряда 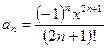, получаем a₀ = x.

Далее определим по рекуррентной формуле a₁ и a₂, сверяя результаты с соответствующими членами ряда:

при n = 0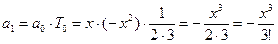

при n = 1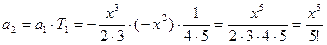

Совпадение полученных значений с членами ряда показывает, что коэффициент рекурсии рассчитан правильно.