Обчислення передаточних функцій дискретних систем в загальному випадку
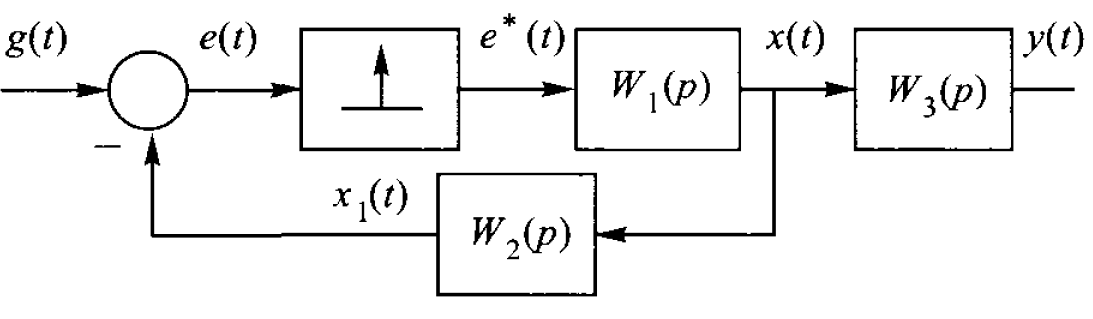
Раніше було розглянуто обчислення передаточних функцій дискретних систем, коли їх еквівалентна схема за найпростішою імпульсною ланкою містить одну безперервну ланка – приведену БЧ [1-9]. Однак може знадобитися обчислення передаточних функцій, еквівалентна схема яких має більш загальний вид (рис. 21.5).
|
| Рис. 21.5 Узагальнена еквівалентна схема дискретної системи |
Знайдемо спочатку передаточні функції  і
і 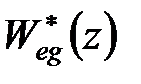 . Використовуючи отриману вище залежність між входом простої імпульсної ланки і виходом наступної за нею безперервної ланки (ПБЧ) в дискретні моменти часу, можемо записати
. Використовуючи отриману вище залежність між входом простої імпульсної ланки і виходом наступної за нею безперервної ланки (ПБЧ) в дискретні моменти часу, можемо записати
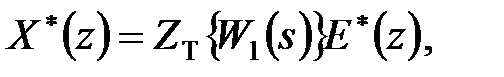
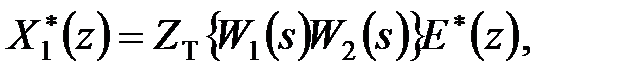
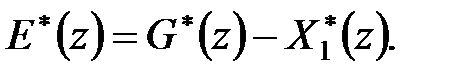
|
Виключимо з цієї системи 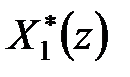
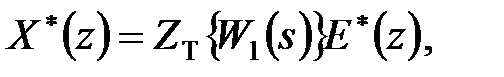

|
З другого рівняння, а також виключивши з двох рівнянь 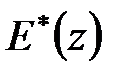 отримаємо відповідно
отримаємо відповідно
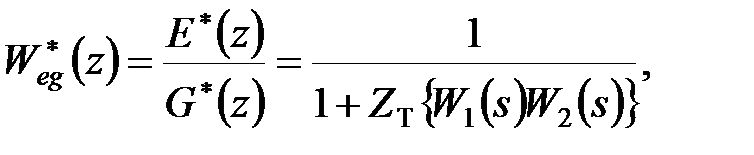
| (21.2) |
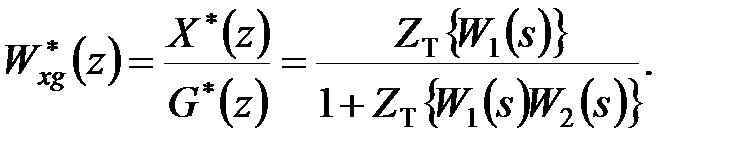
| (21.3) |
Тепер знайдемо передаточну функцію щодо виходу 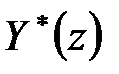 . Для цього замінимо в отриманій вище системі з двох рівнянь перше рівняння рівнянням для
. Для цього замінимо в отриманій вище системі з двох рівнянь перше рівняння рівнянням для 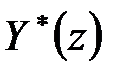
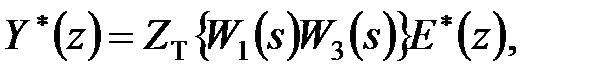
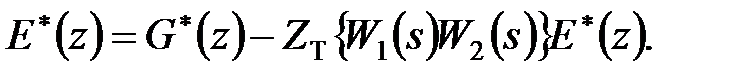
|
Виключивши з цієї системи рівнянь 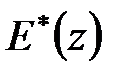 отримаємо
отримаємо
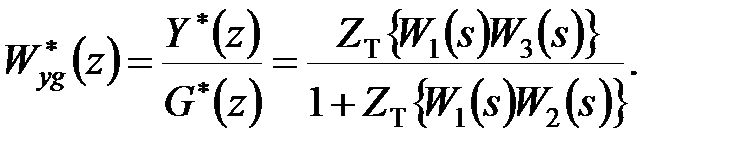
| (21.4) |
З отриманих формул (21.2) – (21.4) виходить наступне правило: передаточна функція щодо входу 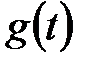 і будь-якого виходу рівна передаточній функції прямого ланцюга, що ділиться на одиницю плюс (а при додатному зворотному зв'язку – мінус) передаточна функція розімкненої системи.
і будь-якого виходу рівна передаточній функції прямого ланцюга, що ділиться на одиницю плюс (а при додатному зворотному зв'язку – мінус) передаточна функція розімкненої системи.
Це правило співпадає з правилом обчислення передаточних функцій одноконтурної безперервної системи. Тільки слід мати на увазі, що при обчисленні передаточної функції прямого ланцюга і передаточної функції розімкненої системи безперервні ланки, розташовані за простою імпульсною ланкою, потрібно розглядати як одну об'єднану ланку. Не можна знаходить 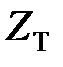 -перетворення передавальних функцій окремих ланок, а потім отримані результати перемножати.
-перетворення передавальних функцій окремих ланок, а потім отримані результати перемножати.
Обчислення передаточної функції системи, що містить дискретно-безперервний фільтр. Ланку, яка описується рівнянням
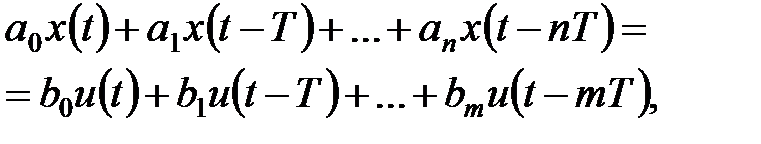
|
називають дискретно-безперервним фільтром.
Переходячи до зображень Лапласа, для дискретно-безперервного фільтру, отримаємо передаточну функцію
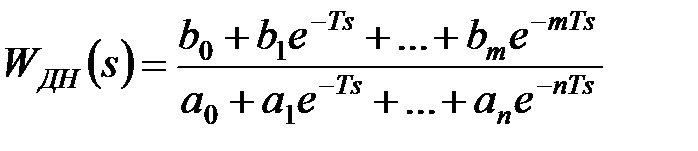
| (21.5) |
Нехай дискретно-безперервний фільтр (ДНФ) включений за дискретним (імпульсним або цифровим) елементом.
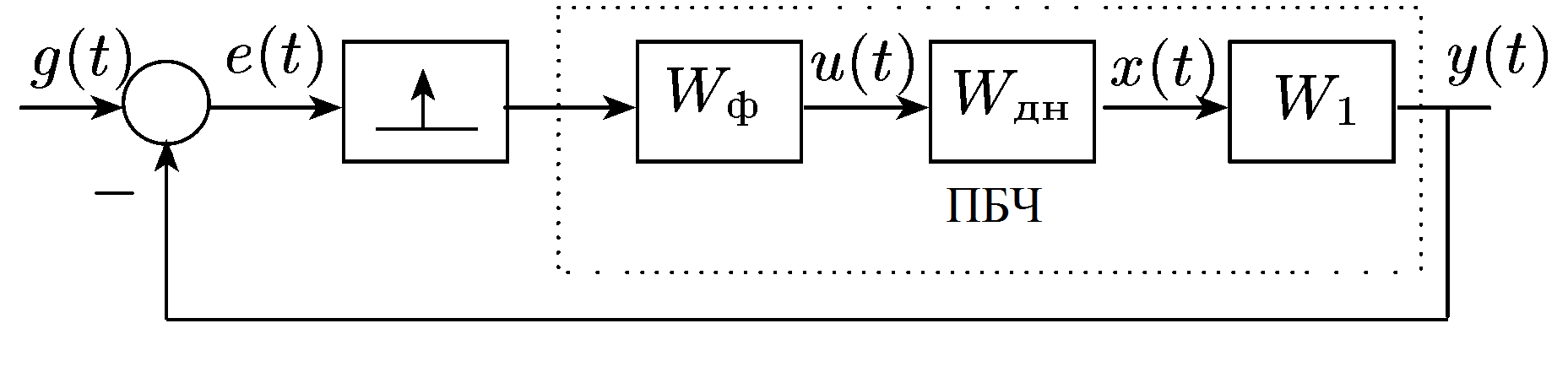
Рис. 21.6. Еквівалентна схема дискретної системи з ДНФ
В цьому випадку по еквівалентній схемі (рис. 21.6) для дискретної передаточної функції розімкненої системи маємо
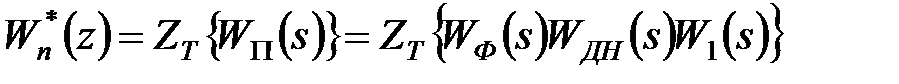 . .
|
Тут  є дробно-раціональною функцією від
є дробно-раціональною функцією від 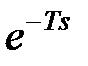 (див. вираз (21.5)). І, як покажемо нижче, в цьому випадку
(див. вираз (21.5)). І, як покажемо нижче, в цьому випадку
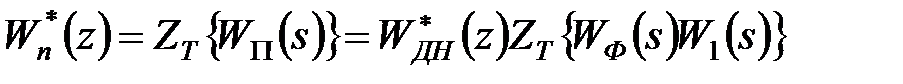 . .
| (21.5) |
де
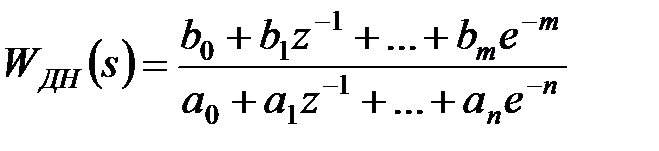 . .
|
Дискретна передаточна функція 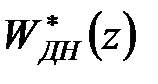 виходить з передаточної функції
виходить з передаточної функції 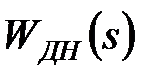 при підстановці
при підстановці 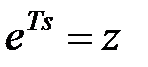 :
:
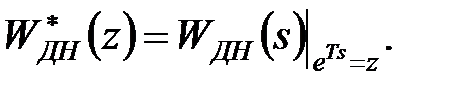
| (21.6) |
Для виведення формули (21.6) співвідношення для передаточної функції ПБЧ має вигляд
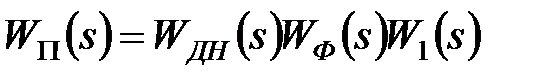 . .
|
підставивши вираз для 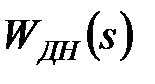 з (21.5), представимо у вигляді
з (21.5), представимо у вигляді
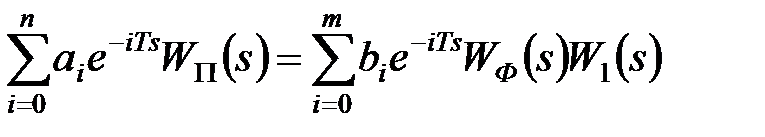 . .
|
Проведемо в обох частинах 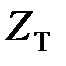 -перетворення. Використовуючи властивість лінійності
-перетворення. Використовуючи властивість лінійності 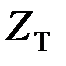 -перетворення і формулу
-перетворення і формулу
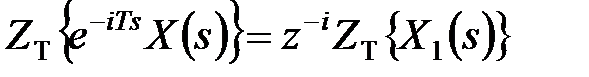 , ,
|
знаходимо
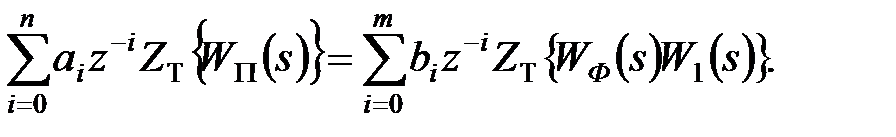
|
Звідси, розділивши обидві частини на суму 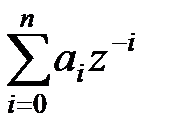 отримаємо (21.5).
отримаємо (21.5).
Отже, ми встановили наступну властивість 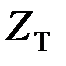 -перетворення: якщо оригінал в
-перетворення: якщо оригінал в 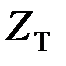 -перетворенні містить множник, що представляє дробно-раціональну функцію від
-перетворенні містить множник, що представляє дробно-раціональну функцію від 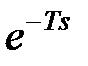 то цей множник можна винести за знак оператора
то цей множник можна винести за знак оператора 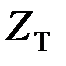 виконавши підстановку
виконавши підстановку 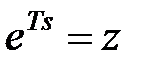 .
.
Якщо ДНФ включений перед дискретним елементом, то, враховуючи, що на роботу останнього впливають значення його вхідної змінної тільки в дискретні моменти, в рівнянні для ДНФ можна покласти 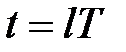 . Тоді отримаємо дискретний фільтр, передаточна функція
. Тоді отримаємо дискретний фільтр, передаточна функція 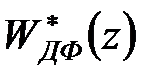 якого співпадає з отриманою вище дискретною передаточною функцією дискретно-безперервного фільтра
якого співпадає з отриманою вище дискретною передаточною функцією дискретно-безперервного фільтра 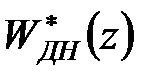 З еквівалентної схеми (рис. 21.7) виходить, що дискретна передаточна функція розімкненої системи виходить такою ж, як і у попередньому випадку.
З еквівалентної схеми (рис. 21.7) виходить, що дискретна передаточна функція розімкненої системи виходить такою ж, як і у попередньому випадку.
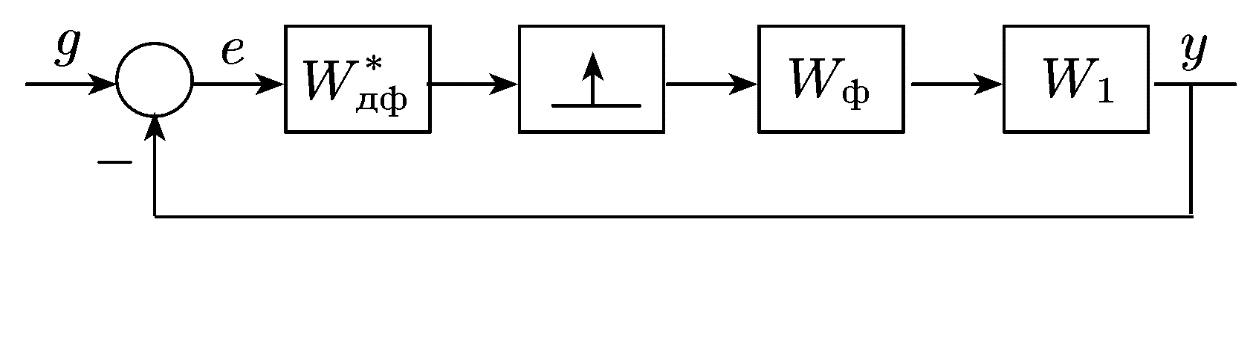
Рис. 21.7. Еквівалентна схема дискретної системи з ДНФ перед дискретним елементом
Таким чином, отримуємо, що при перетворенні структурних схем дискретний елемент і дискретно-безперервний фільтр можна переставляти один з одним.
Тепер розглянемо більш загальну схему з дискретним фільтром (рис. 21.8). Встановлене вище правило обчислення дискретної передаточної функції замкнутої системи залишається в силі і в даному випадку.

Рис. 21.8. Узагальнена еквівалентна схема дискретної системи з дискретним фільтром
При обчисленні передаточної функції розімкненої системи простий імпульсний елемент з послідовними безперервними ланками можна замінити дискретним елементом і представити її дискретну модель у вигляді послідовного з'єднання двох дискретних ланок. Аналогічно можна поступити при обчисленні передаточної функції прямого ланцюга. Тому передаточні функції прямого ланцюга і розімкненої системи дорівнюють добутку передаточних функцій вказаних двох дискретних ланок. Таким чином, маємо

| (21.7а) |
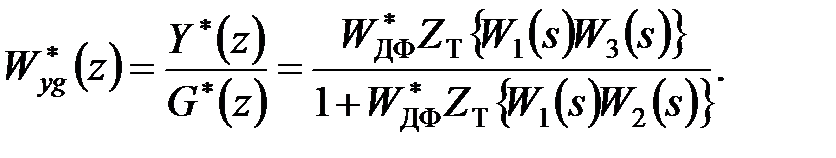
| (21.7б) |
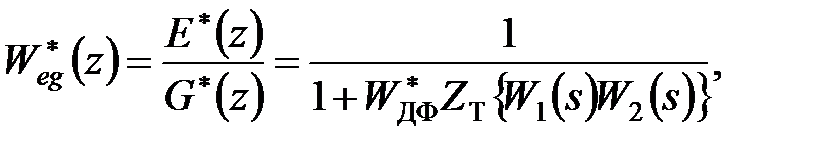
| (21.7в) |
Приклад 21.1. Нехай у дискретній системі, представленій на рис 4.2  ,
, 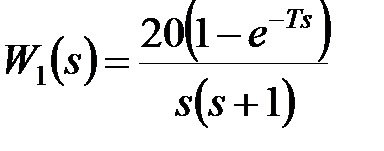 ,
, 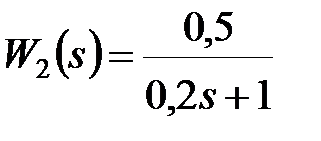 ,
, 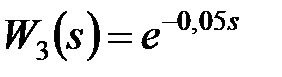 і період проходження імпульсів
і період проходження імпульсів 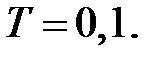 Потрібно визначити передаточні функції
Потрібно визначити передаточні функції 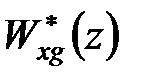 й
й 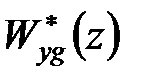 .
.
Знайдемо необхідні для визначення необхідних передаточних функцій 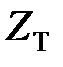 -зображення. Враховуючи, що поліном
-зображення. Враховуючи, що поліном  , як окремий випадок дрібно-раціональної функції від
, як окремий випадок дрібно-раціональної функції від 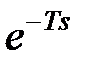 , можна винести за знак оператора
, можна винести за знак оператора 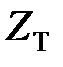 , зробивши підстановку
, зробивши підстановку 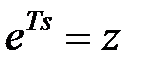 , отримаємо
, отримаємо
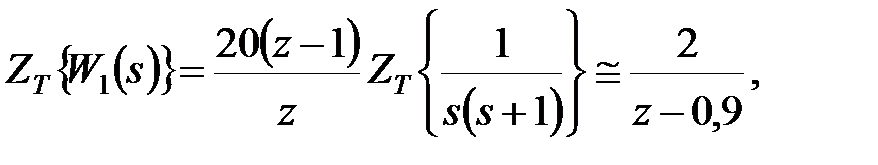
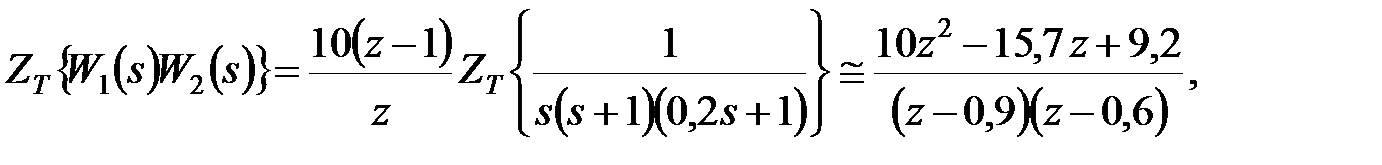
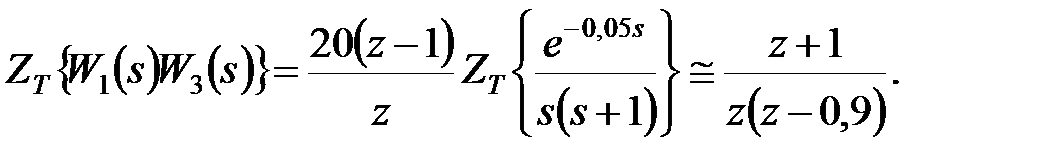
Підставивши отримані вираження й вираження для 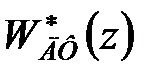 у вищенаведені формули, одержимо
у вищенаведені формули, одержимо
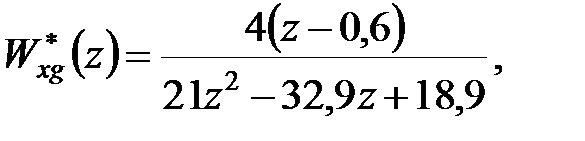
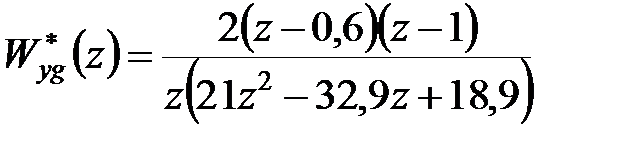
Дата добавления: 2017-08-01; просмотров: 281;
