Распределение Максвелла
| Функцию распределения 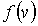 можно представить в виде: можно представить в виде:
где | ||
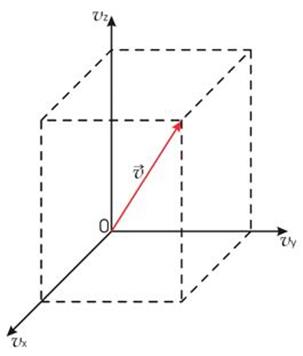
| Рис. 1.Пространство скоростей |
Прологарифмируем выражение (8):
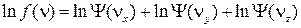 , (9)
, (9)
где 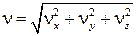 – скорость частицы.
– скорость частицы.
Для решения выражение (9) представим в виде:
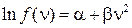 ,
, 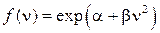 , (10)
, (10)
где a и β – некоторые постоянные.
Соответственно, функция распределения: 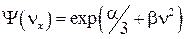 .
.
Функции 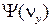 и
и 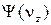 аналогичны. Здесь константы a и β можно определить, исходя из условия нормировки и значения среднего квадрата скорости хаотического движения молекул газа.
аналогичны. Здесь константы a и β можно определить, исходя из условия нормировки и значения среднего квадрата скорости хаотического движения молекул газа.
Коэффициенты примут вид:
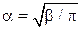 ,
, 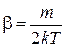 , то есть
, то есть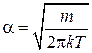 . (11)
. (11)
Таким образом, функция 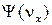 распределения значений проекции скорости vх приобретает форму:
распределения значений проекции скорости vх приобретает форму:
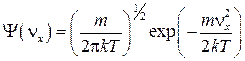 , (12)
, (12)
а функция распределения молекул по скоростям, соответственно, вид
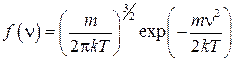 . (13)
. (13)
или
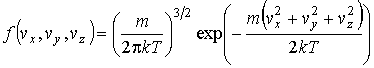 . .
| (14) |
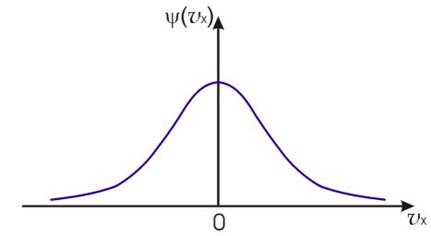
Качественно вид функции (14) совпадает с нормальным законом распределения Гаусса, описывающим распределение ошибок измерений случайной величины.
|
| Рис. 2. |
Вероятность того, что значения проекций скорости лежат внутри элементарного объема пространства скоростей 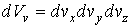 :
:
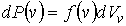 . .
| (15) |
Или
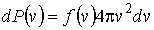 . .
| (16) |
Функция
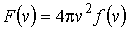 , ,
| (17) |
или
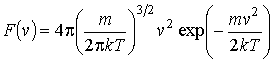 , ,
| (18) |
называется функцией распределения Максвелла по абсолютным значениям скоростей, и она показывает вероятность того, что величина скорости имеет значения от 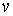 до
до 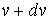 .
.
выражение для наиболее вероятной скорости молекул газа.
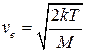 , ,
| (19) |
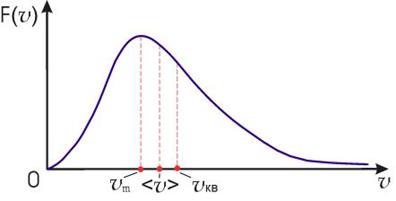
| |
| Рис. 3.Распределение Максвелла по абсолютным значениям скоростей |
Кроме наиболее вероятной скорости, функция 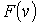 позволяет найти среднюю скорость
позволяет найти среднюю скорость
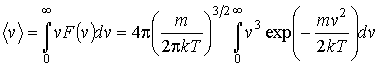
| (20) |
и среднее значение квадрата скорости
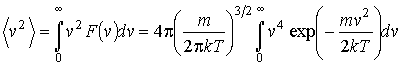 . .
| (21) |
Вычисление интегралов окончательно дает выражения для средней скорости
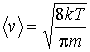
| (22) |
и для средней квадратичной скорости молекул
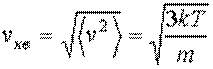 . .
| (23) |
Дата добавления: 2017-06-02; просмотров: 439;

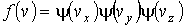 ,
,
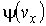 ,
, 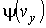 и
и 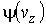 - функции распределения значений соответствующих проекций скорости
- функции распределения значений соответствующих проекций скорости 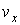 ,
, 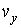 и
и 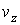 , причем вид этих функций должен быть одинаковым, так как все оси системы координат в пространстве скоростей равноправны.
, причем вид этих функций должен быть одинаковым, так как все оси системы координат в пространстве скоростей равноправны.