Распределение Больцмана. Распределение Максвелла
Источник: Детлаф Яворский 2002 г. П. 10.4-105. С. 132 – 135
Статистический способ описания ТС.
Пусть в результате измерений было установлено, что величина 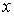 с вероятностью
с вероятностью 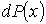 попадает в интервал значений от
попадает в интервал значений от 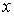 до
до 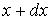 . Тогда можно ввести функцию
. Тогда можно ввести функцию 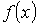 , характеризующую плотность распределения вероятностей:
, характеризующую плотность распределения вероятностей:
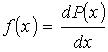 . .
| (1) |
Эта функция в физике обычно называется функцией распределения.
вероятность попадания измеренного значения в весь интервал возможных значений 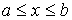 равна единице:
равна единице:
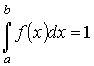 . .
| (2) |
“Это выражение называется условием нормировки функции распределения.
При статистическом описании распределения микрочастиц в пространстве координат 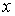 ,
, 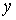 и
и 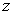 обычно используется не функция распределения
обычно используется не функция распределения 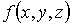 , а концентрация
, а концентрация 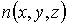 , которая определяется формулой:
, которая определяется формулой:
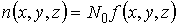 , ,
| (3) |
где 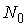 - полное число микрочастиц в объеме системы.
- полное число микрочастиц в объеме системы.
Рассмотрим случай нахождения идеального газа во внешнем гравитационном поле. зависимость давления от высоты:
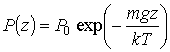 , ,
| (4) |
где 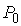 - давление газа на высоте, принятой за начало отсчета.
- давление газа на высоте, принятой за начало отсчета.
Или
. 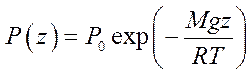
| (5) |
Эта зависимость носит название барометрической формулы.
Подстановка уравнения состояния в выражение (5) позволяет получить следующую зависимость концентрации молекул идеального газа от координаты 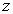 :
:
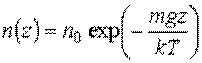 , ,
| (6) |
где 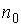 - концентрация газа при
- концентрация газа при 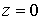 .
.
для однородного гравитационного поля распределение концентрации газа зависит от потенциальной энергии его молекул в этом поле.
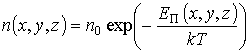 , ,
| (7) |
где 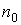 - концентрация газа в точке, соответствующей началу координат при условии, что
- концентрация газа в точке, соответствующей началу координат при условии, что 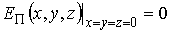 .
.
Дата добавления: 2017-06-02; просмотров: 270;
