Основная тригонометрическая система
Рассмотрим на отрезке 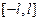 такую систему функций:
такую систему функций:
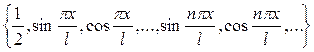
Рассмотрим подробнее, какие у них периоды. Известно, что при умножении на коэффициент частота увеличивается, а соответственно период уменьшается.
Если 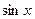 имеет период
имеет период 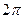 , то
, то 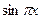 имеет период
имеет период 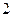 ,
,
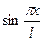 имеет период
имеет период 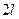 , то есть как раз совершает одно колебание на
, то есть как раз совершает одно колебание на
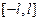 . Впрочем, можно было бы рассматривать и на
. Впрочем, можно было бы рассматривать и на 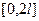 .
.
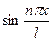 имеет период
имеет период 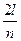 , то есть для двух первых тригонометрических функций (не считая константы, конечно) на этом промежутке укладывается ровно одна волна, а для последующих - кратное число колебаний.
, то есть для двух первых тригонометрических функций (не считая константы, конечно) на этом промежутке укладывается ровно одна волна, а для последующих - кратное число колебаний.
Докажем её ортогональность.
Константа ортогональна любой из функций этой системы, так как
в интегралах 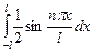 и
и 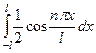 интегрируется функция, у которой целое количество периодов на данном отрезке, и такой интеграл равен 0.
интегрируется функция, у которой целое количество периодов на данном отрезке, и такой интеграл равен 0.
Ортогональность всех остальных функций доказывается по формулам тригонометрии:
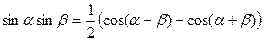
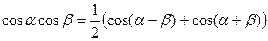
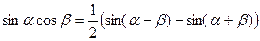 .
.
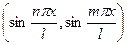 =
= 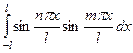 =
=
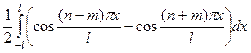 но так как
но так как 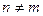 (мы же взяли разные функции из системы) то будет
(мы же взяли разные функции из системы) то будет 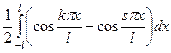 то есть разность интегралов, каждый из которых 0 в силу того, что там периодическая функция, у которой на промежутке укладывается целое число полных периодов.
то есть разность интегралов, каждый из которых 0 в силу того, что там периодическая функция, у которой на промежутке укладывается целое число полных периодов.
Для двух косинусов аналогично: 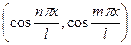 =
= 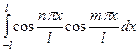 =
= 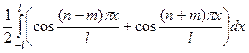 = 0.
= 0.
Для синуса и косинуса 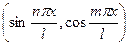 =
= 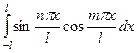 =
=
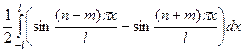 = 0 .
= 0 .
А если умножать не разные функции, а одну и ту же, то получится квадрат нормы. Посчитаем квадраты норм всех функций:
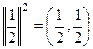 =
= 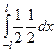 =
= 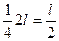 .
.
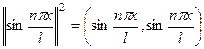 =
= 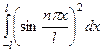 =
= 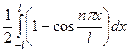 =
=
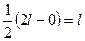 .
.
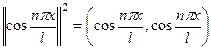 =
= 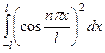 =
= 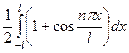 =
=
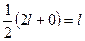 .
.
Ряд Фурье: 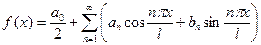
его коэффициенты:
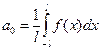 ,
, 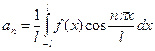 ,
, 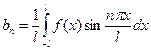 .
.
Ряд Фурье с помощью синусов и косинусов разных частот осуществляет наилучшее приближении графика функции, в том смысле, что наименьшее среднеквадратичное отклонение. Для частичных сумм ряда, чем больше взято частот, тем более мелкие особенности графика будут учтены, и огибающая пройдёт ближе.
Докажем, что ряд Фурье имеет именно такое строение. Вспомним общую формулу 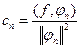 . У нас в данном случае квадрат нормы равен
. У нас в данном случае квадрат нормы равен 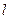 для этой конкретной системы. Скалярное произведение определяется через интеграл. Поэтому
для этой конкретной системы. Скалярное произведение определяется через интеграл. Поэтому 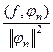 в этом случае имеет вид
в этом случае имеет вид 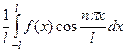 . Подробнее рассмотрим коэффициент
. Подробнее рассмотрим коэффициент 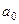 .
.
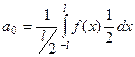 =
= 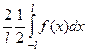 =
= 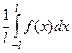 .
.
Дата добавления: 2017-06-02; просмотров: 1074;
