Максимальное, среднее и среднеквадратичное отклонение.

Чтобы исследовать взаимосвязь 2 функций, а именно, удаление их графиков друг от друга, можно использовать такую величину:

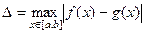называемую «равномерным», или максимальным, отклонением между графиками. Однако это не совсем точно характеризует взаимосвязь пары функций, ведь они могут идти очень близко, а затем удалиться на коротком интервале, а отклонение будет считаться большим. Например, как на чертеже:

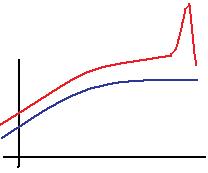
Вместо этого можно рассматривать среднее значение модуля разности, и это уже более точная оценка.

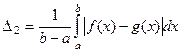- среднее отклонение.

Но чтобы посчитать интеграл от модуля, надо искать точки пересечения и разбивать интервал на части. Чтобы избежать этих громоздких вычислений, можно рассматривать такую величину:

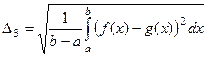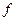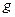среднеквадратичное отклонение между и . Когда среднее стремится к 0, то и среднеквадратичное тоже, и хотя они не прямо пропорциональны, но минимальное значение одной из этих величин достигается при тех же условиях, что и у другой.

Если домножить функции из системы на какие-то коэффициенты, то получится выражение 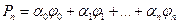многочлен по ортогональной системе.

Теорема. Среднеквадратичное отклонение между 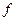и 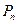минимально 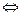коэффициенты 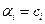(совпадают с коэффициентами Фурье).

Доказательство. 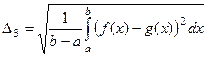минимально тогда и только тогда, когда 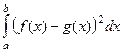минимально, так что мы можем рассмотреть просто интеграл от квадрата разности, то есть величину 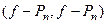. Во-первых, она по построениею больше или равна 0. Рассмотрим её подробнее:

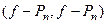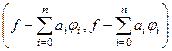= применим свойства скалярного произведения, будет так:

=

.

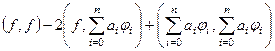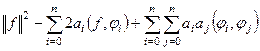Но от двойной суммы где (n+1)² слагаемых, фактически остаётся только (n+1) так как при несовпадении номера, скалярные произведения 0, ведь это ортогональная система.

=

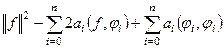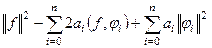
преобразуем 2-е слагаемое по формуле .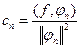

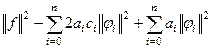теперь прибавим и вычтем такое слагаемое, чтобы образовать разность квадратов:

=

=

.

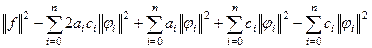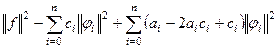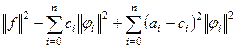Это выражение минимально, когда разность 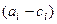равна 0, то есть в точности, когда 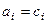что и требовалось доказать.

Отсюда следует неравенство Бесселя: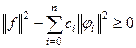

При 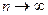получается равенство 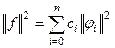, которое называется уравнением замкнутости.

Аналоги в векторных пространствах: если рассмотреть неполную сумму квадратов координат какого-то вектора, то очевидно, она меньше, чем квадрат его модуля. Так, для вектора из 3 координат

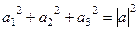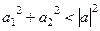, . Так и здесь, если рассматривать не всю систему функций, а всего лишь до номера n то получим неравенство, а если всю - то равенство.

Кстати, с помощью скалярных произведений и норм можно доказать аналог теоремы Пифагора для систем функций.

Если 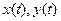ортогональные функции, то :

=

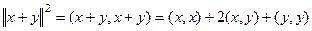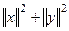
для векторов такое равенство означало,что квадрат гипотенузы равен сумме квадратов катетов.