Ортогональные функции.
Две функции называются ортогональными на интервале 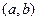 , если
, если 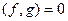 , то есть
, то есть 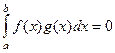 .
.
Здесь нет такого простого геометрического смысла, как в случае перпендикулярных векторов, для функций ортогональность значит, что произведение функций где-то больше, а где-то меньше нуля так, чтобы эти части компенсировались и уничтожились при интегрировании.
Пример. Доказать, что функции 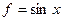 ,
, 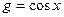 ортогональны на интервале
ортогональны на интервале 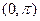 .
.
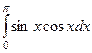 =
= 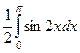 =
= 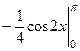 =
= 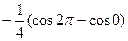 = 0.
= 0.
Замечание. Если одна из функций в произведении тождественно равна 0, то интеграл очевидно, равен 0. Поэтому тождественный 0 это ортогональная всем функция.
Ортогональные системы.Если любая пара функций в системе ортогональна, то система называется ортогональной.
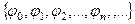 ортогональна, если
ортогональна, если 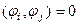 для любых
для любых 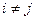 .
.
Система функций на отрезке 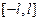 :
:
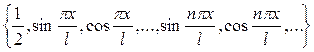
ортогональна, её подробно рассмотри позже, с помощью неё как раз и строятся тригонометрические ряды Фурье.
Формулы коэффициента (Фурье) разложения по ортогональной системе: 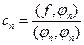 или
или 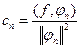 .
.
Доказательство.Пусть функция 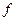 представлена в виде суммы:
представлена в виде суммы: 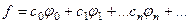 найдём коэффициенты .
найдём коэффициенты .
Можно скалярно домножить на 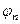 . Получим
. Получим
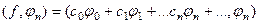 =
= 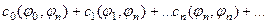
среди этих слагаемых, лишь одно отлично от нуля, ведь система ортогональна, и при 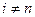 будет
будет 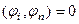 .
.
Тогда 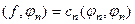 , тогда
, тогда 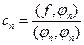 то есть
то есть 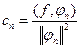 .
.
Можно записать и с помощью интегралов: 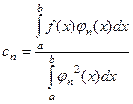 .
.
Аналогичное равенство верно и для векторов: 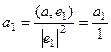 .
.
Дата добавления: 2017-06-02; просмотров: 3462;
