Теорема Эйлера-2. Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.

Пример 3.35 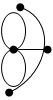Вспомним задачу о кенигсбергских мостах. Она сводится к вопросу – является ли граф, представляющий эту задачу, эйлеровым? Если вершины будут обозначать участки суши, а ребра – мосты, то получим граф следующего вида:
Очевидно, что этот граф не эйлеров, т.к. все его вершины имеют нечетные степени; поэтому требуемый цикл не существует. Если отменить требование возврата в ту же точку, то вопрос о пути по всем мостам сведется к вопросу о существовании собственной эйлеровой цепи.

Теорема 3.4 Граф имеет собственную эйлерову цепь (путь) Û когда он связный и ровно две его вершины имеют нечетную степень.

Вершины нечетной степени являются началом и концом эйлеровой цепи.

Если снова вернуться к рассмотренному примеру, то увидим, что эйлерова цепь в нем также не существует, т. к. вершин нечетной степени в нем 4.

А теперь разберемся, как найти эйлеров цикл. Сначала еще определение.

Мостом (или перешейком) называется такое ребро графа G, удаление которого увеличивает число связных компонент. Если ребро r принадлежит некоторому циклу C, то оно не может быть мостом.

Пример 3.36 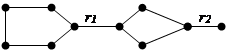В данном графе ребра r₁ и r₂ являются мостами.

Для нахождения эйлеровой цепи в связном графе, который имеет вершины только четной степени, используют алгоритм Флери:

1) Движение начинается из произвольной вершины графа; идем по ребрам, включая эти ребра в эйлерову цепь и удаляя их из графа.

2) В очередной вершине выбираем путь по перешейку только в том случае, если нет пути по циклу.

3) Если в графе остаются ребра, которые нельзя использовать для продолжения имеющегося пути, то следует начать строить простой замкнутый цикл из уже пройденной вершины и инцидентного ей ребра, если последнее ранее не использовалось.

Пример 3.37 Пусть требуется построить эйлеров цикл для графа, изображенного на рисунке. Начать построение эйлерового цикла можно с любого ребра графа. Начиная с е₁, получим цикл v₁, e₁, v₅, e₂, v₄ ,e₃, v₃ ,e₄ , v₄ ,e₅ ,v₁,e₆ ,v₃, e₈, v₂, e₇ ,v₁. В данном случае сразу получили эйлерову цепь.

3.5.5 Гамильтоновы графы

Гамильтонова цепь (путь) – это простая цепь (путь), которая проходит через каждую вершину (узел) графа ровно по одному разу. Соответственно гамильтонов цикл – это простой цикл, который проходит через каждую вершину графа.

Граф, содержащий гамильтонов цикл, называется гамильтоновым графом.

Пример 3.38 Гиперкуб порядка n при n ³ 3 имеет гамильтонов цикл. Этот цикл описывается кодом Грея (каждые два соседних набора отличаются ровно одним разрядом Þ на графе они соединены ребром). (000, 001, 011, 111, 101, 100, 110, 010, 000).

В отличие от эйлерова графа, не существует четкого критерия для определения, является ли граф гамильтоновым.

В качестве практического применения задачи поиска гамильтонова пути можно назвать т.н. задачу коммивояжера. В ней требуется осуществить обход всех населенных пунктов, посещая каждый по разу, и при этом постараться пройти минимальное расстояние.

Глава 2 Булева алгебра

Глава 3 Конечные автоматы