Математическая оценка устойчивости

Как указывалось ранее, все системы автоматического управления должны обладать устойчивостью. САУ считается устойчивой, если при ограниченном входном сигнале реакция системы в виде выходного сигнала будет также ограниченной. Большинство САУ имеет замкнутую систему с отрицательной обратной связью. В такой системе выходная величина через систему обратной связи подается на вход, где сравнивается с задающим воздействием. При этом нормально выполняющая свои функции система устраняет расхождение между задающим и выходным сигналом, обеспечивая некоторое допустимое отклонение характерное для устойчивой системы. Для неустойчивой системы это отклонение будет возрастать с течением времени.

При исследовании замкнутой САУ на устойчивость из-за удобства математических исследований, рассматривают так называемое свободное движение системы. Свободное движение системы определяется свойствами системы после подачи и снятия входного возмущающего сигнала.

Русский ученый А.М. Ляпунов на примере механической системы показал, что если система, движущаяся свободно будет устойчивой, то будет устойчивой и система, на которую действуют возмущения.

Распространяя этот вывод на САУ, для математического описания устойчивости может рассматриваться способность системы в результате возмущенного движения приходить к невозмущенному состоянию после того как действие возмущения прекратилось.

Пусть выходные s сигналы при отсутствии возмущении характеризуется функциями 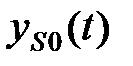(s=0,1,…,n), а при действии возмущений – функциями .

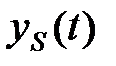Отклонение возмущенного движения от установившегося (свободного)

= -

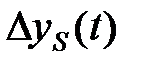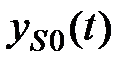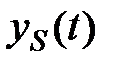
Знак (–) обозначает обратную отрицательную связь. В начальный момент отклонение будет .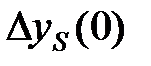

Математически условие устойчивости можно сформулировать так: невозмущенное движение будет устойчивым, если для всякого положительного малого числа μ можно подобрать другое число ς , зависящее от μ , что для всех возмущенных движений при начальных условиях

,

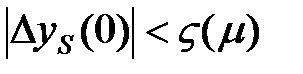для всех t > 0 выполняется неравенство

.

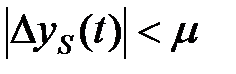Если 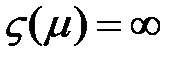, то система называется неограниченно устойчивой, т. е. она устойчива при любых начальных условиях.

Свободное движение замкнутой системы описывается следующим дифференциальным уравнением:

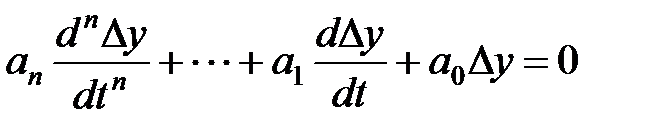, (7.1)

при начальных условиях 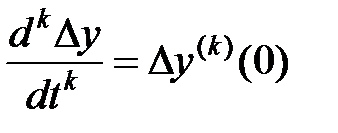, где k = 0,1,…,n.

Решение дифференциального уравнения (7.1) представляет выражение

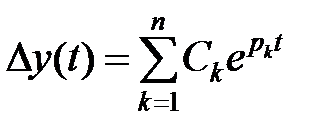, (7.2)

где С_k - зависящая от начальных условий постоянная интегрирования,

p_K – корни характеристического уравнения

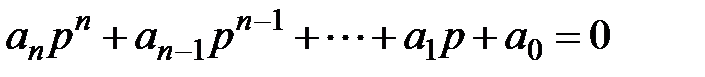. (7.3)

Чтобы система была устойчивой при решение (7.2 ) должно выполняться условие

.

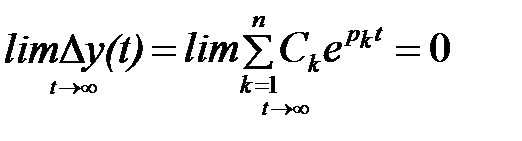Из этого следует, что необходимым и достаточным условием устойчивости линейной САУ является то, что все корни (действительные и вещественная часть комплексных корней) характеристического уравнения будут отрицательными.

Характеристические уравнения (7.3) могут быть получены по дифференциальным уравнениям системы или из передаточных функций.

Как указывалось выше, при исследовании на устойчивость замкнутой САУ рассматривается САУ в свободном состоянии. На рис. 7.1. показана структурная схема простейшей замкнутой САУ в свободном состоянии, которая составлена из обьекта управления и регулятора с передаточными функциями, соответственно – W₀(s), W_p(s).

При исследовании на устойчивость исходными являются передаточные функции замкнутой системы или условно разомкнутой системы. В зависимости от того, какая из ПФ имеет более простое выражение.

На рис. 7.1. показан прием условного размыкания замкнутой цепи.

Выражение ПФ замкнутой САУ может быть получено из формулы 6.7 в виде

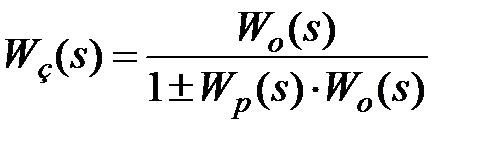. (7.4)

Выражение ПФ разомкнутой САУ согласно (6.7) имеет вид

.

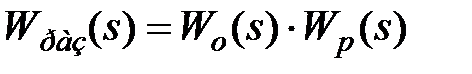С другой стороны ПФ разомкнутой системы можно представить в виде отношения комплексных полиномов т.е.:

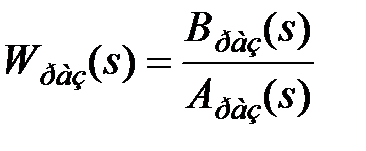(7.5)

Подставив в знаменатель выражения (5.4) вместо сомножителей W_раз(s), получим в случае отрицательной обратной связи

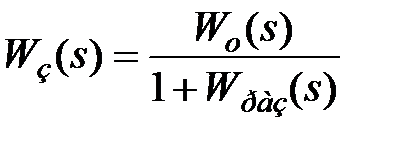. (7.6)

Если в выражении (7.4) представить каждый из сомножителей ПФ в виде отношении многочленов 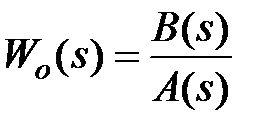, , 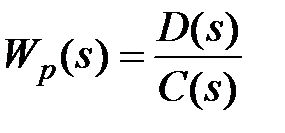сложить числители и знаменатели и сумму приравнять нулю, то получим алгебраическое уравнение высокого порядка:

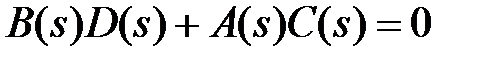
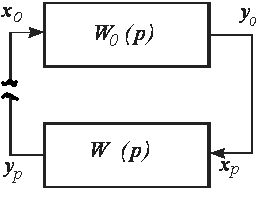
Рис.7.1. Укрупненная схема САУ

Аналитическое решение характеристических уравнений с целью определения знаков корней, особенно когда они представляют алгебраические уравнения высокого порядка требует больших затрат и являются громоздкими. Поэтому в ТАУ используются косвенные методы, позволяющие определить знаки корней характеристического уравнения без решения этих уравнений. Эти методы в зависимости от исходных данных используют следующие критерии: Рауса-Гурвица, Михайлова, Найквиста, диаграмму Боде (ЛАЧХ) и др.